2024年广东省数学八(下)期末复习:精选压轴题(3)
试卷更新日期:2024-06-02 类型:复习试卷
一、单选题
-
1. 如图,一次函数 的图象分别与x轴、y轴交于 两点,过原点O作 垂直于直线 交 于点 ,过点 作 垂直于x轴于点 ,过点 作 垂直于直线 交 于点 ,过点 过点作 垂直于x轴于点 ……依此规律作下去,则点 的坐标是( )
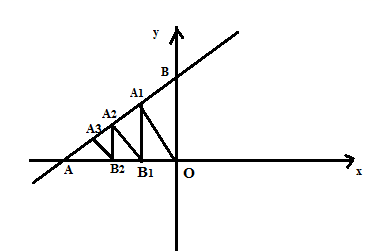 A、 B、 C、 D、2. 如图1所示,四边形为正方形,对角线 , 相交于点 , 动点在正方形的边和对角线上匀速运动.如果点运动的时间为 , 点与点的距离为 , 且表示与的函数关系的图象大致如图2所示,那么点的运动路线可能为( )
A、 B、 C、 D、2. 如图1所示,四边形为正方形,对角线 , 相交于点 , 动点在正方形的边和对角线上匀速运动.如果点运动的时间为 , 点与点的距离为 , 且表示与的函数关系的图象大致如图2所示,那么点的运动路线可能为( ) A、 B、 C、 D、3. 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( )
A、 B、 C、 D、3. 由四个全等的直角三角形拼成如图所示的“赵爽弦图”,若直角三角形斜边长为2,最短的之边长为1,则图中阴影部分的面积为( ) A、1 B、3 C、4﹣2 D、4+24. 如图,点B , C , E在同一直线上,分别以为边作正方形和正方形 , , H是的中点,那么的长是( )
A、1 B、3 C、4﹣2 D、4+24. 如图,点B , C , E在同一直线上,分别以为边作正方形和正方形 , , H是的中点,那么的长是( ) A、 B、 C、 D、5. 一次函数的图象如图所示,点在该函数的图象上,则不等式的解集为( )
A、 B、 C、 D、5. 一次函数的图象如图所示,点在该函数的图象上,则不等式的解集为( ) A、 B、 C、 D、6. 数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( )
A、 B、 C、 D、6. 数形结合是解决数学问题常用的思想方法.如图,一次函数y=kx+b(k、b为常数,且k<0)的图象与直线y=x都经过点A(3,1),当kx+b<x时,x的取值范围是( ) A、x>3 B、x<3 C、x<1 D、x>17. 如图,矩形中, , , 把矩形沿对角线所在直线折叠,使点落在点处,交于点 , 连接 . 则以下结论:① , ② , ③ , ④是等腰三角形,其中正确的个数是( )
A、x>3 B、x<3 C、x<1 D、x>17. 如图,矩形中, , , 把矩形沿对角线所在直线折叠,使点落在点处,交于点 , 连接 . 则以下结论:① , ② , ③ , ④是等腰三角形,其中正确的个数是( )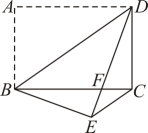 A、1 B、2 C、3 D、48. 一次函数y=ax+b与y=cx+d的图象如图所示,下列说法:
A、1 B、2 C、3 D、48. 一次函数y=ax+b与y=cx+d的图象如图所示,下列说法:① 对于函数y=-ax+b来说,y随x的增大而增大; ②函数y=ax+d不经过第四象限;③不等式ax-d≥cx-b的解集是x≥4;④ 4(a-c)=d-b。其中正确的有( )
 A、4个 B、3个 C、2个 D、1个9. 一张矩形纸片 , 已知 , , 小明按如图所示的步骤折叠纸片,则的长为( )
A、4个 B、3个 C、2个 D、1个9. 一张矩形纸片 , 已知 , , 小明按如图所示的步骤折叠纸片,则的长为( ) A、4 B、2 C、 D、10. 如图,在四边形 中,点P是边 上的动点,点Q是边 上的定点,连接 , 分别是 的中点,连接 .点P在由C到D运动过程中,线段EF的长度( )
A、4 B、2 C、 D、10. 如图,在四边形 中,点P是边 上的动点,点Q是边 上的定点,连接 , 分别是 的中点,连接 .点P在由C到D运动过程中,线段EF的长度( ) A、保持不变 B、逐渐变小 C、先变大,再变小 D、逐渐变大11. 如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF= ;④S△AEF= .其中正确的有( )
A、保持不变 B、逐渐变小 C、先变大,再变小 D、逐渐变大11. 如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF= ;④S△AEF= .其中正确的有( ) A、1个 B、2个 C、3个 D、4个12. 一根长、宽的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后, , 则最初折叠时,的长为( )
A、1个 B、2个 C、3个 D、4个12. 一根长、宽的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后, , 则最初折叠时,的长为( ) A、 B、 C、 D、13. 如图,在平面直角坐标系中,直线的解析式为 , 直线的解析式为 , 直线交轴于点 , 以为边作第一个等边三角形 , 交直线于点 , 过点作轴的平行线交直线于点 , 以为边作第二个等边三角形△ , 交直线于点 , , 顺次这样做下去,第2020个等边三角形的边长为( )
A、 B、 C、 D、13. 如图,在平面直角坐标系中,直线的解析式为 , 直线的解析式为 , 直线交轴于点 , 以为边作第一个等边三角形 , 交直线于点 , 过点作轴的平行线交直线于点 , 以为边作第二个等边三角形△ , 交直线于点 , , 顺次这样做下去,第2020个等边三角形的边长为( ) A、 B、 C、4038 D、4040
A、 B、 C、4038 D、4040二、填空题
-
14. 如图,正方形中,在的延长线上取点使 , 连接分别交于 , 下列结论:
①;②;③;④图中有8个等腰三角形.
其中正确的有 (填序号),
 15. 如图1,在矩形中,动点P从点B出发,沿、、运动至点A停止,设点P运动的路程为 , 的面积为 , 如果关于的函数图象如图2所示,则矩形的周长是 .
15. 如图1,在矩形中,动点P从点B出发,沿、、运动至点A停止,设点P运动的路程为 , 的面积为 , 如果关于的函数图象如图2所示,则矩形的周长是 . 16. 如图,在平面直角坐标系xOy中,ABC的顶点B,C的坐标分别为(- , 0),(2 , 0),点A在y轴上,点D为AC的中点,DE⊥AB于点E,若∠ABD=∠DBC,则DE= .
16. 如图,在平面直角坐标系xOy中,ABC的顶点B,C的坐标分别为(- , 0),(2 , 0),点A在y轴上,点D为AC的中点,DE⊥AB于点E,若∠ABD=∠DBC,则DE= . 17. 如图,在矩形中,对角线、的交点为 , 矩形的长、宽分别为、 , 过点分别交、于、 , 那么图中阴影部分面积为 .
17. 如图,在矩形中,对角线、的交点为 , 矩形的长、宽分别为、 , 过点分别交、于、 , 那么图中阴影部分面积为 . 18. 如图,已知平面直角坐标系中有一点 , 且一次函数与x轴相交于点B,与y轴相交于点C,在直线上存在一动点M,连接 , , 当点M运动到最短时,的长度是 .
18. 如图,已知平面直角坐标系中有一点 , 且一次函数与x轴相交于点B,与y轴相交于点C,在直线上存在一动点M,连接 , , 当点M运动到最短时,的长度是 .
19. 如图1,在菱形ABCD中,动点P从点C出发,沿着C→A→D运动至终点D , 设点P运动的路程为x , △BCP的面积为y , 若y与x的函数图象如图2所示,则图中的值为 . 20. 如图,在边长为的等边中,分别取三边的中点 , , , 得;再分别取三边的中点 , , , 得;这样依次下去 , 经过第次操作后得 , 则的面积为 .
20. 如图,在边长为的等边中,分别取三边的中点 , , , 得;再分别取三边的中点 , , , 得;这样依次下去 , 经过第次操作后得 , 则的面积为 . 21. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .
21. 菱形ABCD,点A,B,C,D均在坐标轴上. ∠ABC=120°,点A(-6,0),点E是CD的中点,点P是OC上的一动点,则△PDE周长的最小值是 .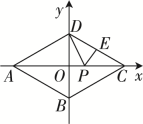
三、解答题
-
22. 如图1,点C、D是线段AB同侧两点,且AC=BD,∠CAB=∠DBA,连接BC,AD交于点E.
 (1)、求证:AE=BE;(2)、如图2,△ABF与△ABD关于直线AB对称,连接EF.
(1)、求证:AE=BE;(2)、如图2,△ABF与△ABD关于直线AB对称,连接EF.①判断四边形ACBF的形状,并说明理由;
②若∠DAB=30°,AE=5,DE=3,求线段EF的长.
23. 已知,如图①,在中, , , 点E为上的一动点,连接 , 过点C作于点H , 以为腰作等腰直角连接 . (1)、求证:四边形为正方形;(2)、如图②,当D , H , G三点共线时,求的值;(3)、求的最小值.24. 如图1,在正方形中, , 点在边上,连接 , 且 , 点是的中点.
(1)、求证:四边形为正方形;(2)、如图②,当D , H , G三点共线时,求的值;(3)、求的最小值.24. 如图1,在正方形中, , 点在边上,连接 , 且 , 点是的中点. (1)、求的长;(2)、过点作直线 , 分别交 , 于点 , , 且 , 求的长;(3)、如图2,过点作的垂线,分别交 , , 于点 , , , 连接 , 求的度数.25. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,将线段绕点A顺时针旋转 , 得到线段 , 过点B,C作直线,交x轴于点D.
(1)、求的长;(2)、过点作直线 , 分别交 , 于点 , , 且 , 求的长;(3)、如图2,过点作的垂线,分别交 , , 于点 , , , 连接 , 求的度数.25. 如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点B,将线段绕点A顺时针旋转 , 得到线段 , 过点B,C作直线,交x轴于点D.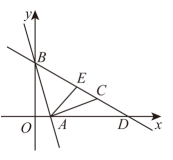 (1)、点C的坐标为▲;求直线的表达式;(2)、若点E为线段上一点,且△ABE的面积为 , 求点E的坐标;(3)、在(2)的条件下,在平面内是否存在点P,使以点A,B,E,P为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.26. 如图,直线与x轴、y轴分别交于点 , 点P在x轴上运动,连接 , 将沿直线折叠,点O的对应点记为 .
(1)、点C的坐标为▲;求直线的表达式;(2)、若点E为线段上一点,且△ABE的面积为 , 求点E的坐标;(3)、在(2)的条件下,在平面内是否存在点P,使以点A,B,E,P为顶点的四边形为平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.26. 如图,直线与x轴、y轴分别交于点 , 点P在x轴上运动,连接 , 将沿直线折叠,点O的对应点记为 .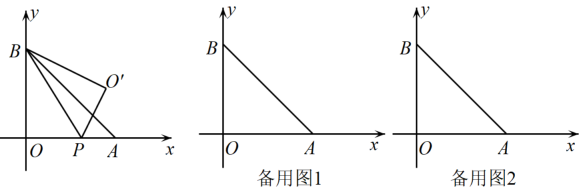 (1)、求k、b的值;(2)、若点恰好落在直线上,求的面积;(3)、将线段绕点P顺时针旋转45°得到线段 , 直线与直线的交点为Q , 在点P的运动过程中,是否存在某一位置,使得为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.27. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于点A , B , 且点A的坐标为 , 四边形是正方形.
(1)、求k、b的值;(2)、若点恰好落在直线上,求的面积;(3)、将线段绕点P顺时针旋转45°得到线段 , 直线与直线的交点为Q , 在点P的运动过程中,是否存在某一位置,使得为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.27. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于点A , B , 且点A的坐标为 , 四边形是正方形. (1)、填空:;(2)、求点D的坐标;(3)、若点P是线段上的一个动点(点A , B除外),试探究:在x上方是否存在另一个点Q , 使得以O , B , P , Q为顶点的四边形是菱形?若存在,请求出点Q的坐标;若不存在,请说明理由.28. 如图1,已知四边形ABCD是正方形,E是对角线BD上的一点,连接AE,CE.
(1)、填空:;(2)、求点D的坐标;(3)、若点P是线段上的一个动点(点A , B除外),试探究:在x上方是否存在另一个点Q , 使得以O , B , P , Q为顶点的四边形是菱形?若存在,请求出点Q的坐标;若不存在,请说明理由.28. 如图1,已知四边形ABCD是正方形,E是对角线BD上的一点,连接AE,CE. (1)、求证:AE=CE;(2)、如图2,点P是边CD上的一点,且PE⊥BD于E,连接BP,O为BP的中点,连接EO.若∠PBC=30°,求∠POE的度数;(3)、在(2)的条件下,若OE= , 求CE的长.29. 如图,是的中线,是线段上一点(不与点重合).交于点 , , 连接 .
(1)、求证:AE=CE;(2)、如图2,点P是边CD上的一点,且PE⊥BD于E,连接BP,O为BP的中点,连接EO.若∠PBC=30°,求∠POE的度数;(3)、在(2)的条件下,若OE= , 求CE的长.29. 如图,是的中线,是线段上一点(不与点重合).交于点 , , 连接 . (1)、如图1,当点与重合时,证明;(2)、如图1,当点与重合时,求证:四边形是平行四边形;(3)、如图2,当点不与重合时,(2)中的结论还成立吗?请说明理由.30. 已知,在等边三角形中,点E在上,点D在的延长线上,且 .
(1)、如图1,当点与重合时,证明;(2)、如图1,当点与重合时,求证:四边形是平行四边形;(3)、如图2,当点不与重合时,(2)中的结论还成立吗?请说明理由.30. 已知,在等边三角形中,点E在上,点D在的延长线上,且 . (1)、【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系,请你直接写出结论: (填“>”、“<”或“=”).(2)、【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与的大小关系,请你写出结论,并说明理由. ▲ (填“>”、“<”或“=”);理由如下,过点E作 , 交于点F . (请你完成以下解答过程).(3)、【拓展结论,设计新题】在等边三角形中,点E在直线上,点D在线段的延长线上,且 , 若的边长为1, , 求的长(直接写出结果).31. 在正方形中,点、 分别是、上的中点,连接、 , 与相交于点(如图1)
(1)、【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系,请你直接写出结论: (填“>”、“<”或“=”).(2)、【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与的大小关系,请你写出结论,并说明理由. ▲ (填“>”、“<”或“=”);理由如下,过点E作 , 交于点F . (请你完成以下解答过程).(3)、【拓展结论,设计新题】在等边三角形中,点E在直线上,点D在线段的延长线上,且 , 若的边长为1, , 求的长(直接写出结果).31. 在正方形中,点、 分别是、上的中点,连接、 , 与相交于点(如图1) (1)、求证:;(2)、如图2,连接 , 取中点 , 连接(如图),若正方形边长为 , 则(直接写出答案);(3)、平移图1中线段 , 使点与点重合,点在线段的延长线上,连接 , 取中点 , 连接(如图),请猜想线段与线段的数量关系,并证明你的猜想.32. 已知正方形ABCD,以CE为边在正方形ABCD外部作正方形CEFG,连接AF,点H是AF的中点,连接BH,HE
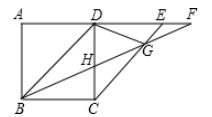
(1)、求证:;(2)、如图2,连接 , 取中点 , 连接(如图),若正方形边长为 , 则(直接写出答案);(3)、平移图1中线段 , 使点与点重合,点在线段的延长线上,连接 , 取中点 , 连接(如图),请猜想线段与线段的数量关系,并证明你的猜想.32. 已知正方形ABCD,以CE为边在正方形ABCD外部作正方形CEFG,连接AF,点H是AF的中点,连接BH,HE (1)、如图所示,点E在边CB上时,则BH,HE的关系为;(2)、如图所示,点在BC延长线上,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请给出新的结论并证明。(3)、如图,点B、E、F在同一条直线上,求证:.33. 如图,在平面直角坐标系中,矩形的顶点A在x轴正半轴,点D在矩形的边上,与相交于点G , , 对角线解析式为: .
(1)、如图所示,点E在边CB上时,则BH,HE的关系为;(2)、如图所示,点在BC延长线上,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请给出新的结论并证明。(3)、如图,点B、E、F在同一条直线上,求证:.33. 如图,在平面直角坐标系中,矩形的顶点A在x轴正半轴,点D在矩形的边上,与相交于点G , , 对角线解析式为: . (1)、求D点坐标和k的值;(2)、平行于x轴的直线m , 从原点O出发,以每秒1个单位长度的速度沿方向移动,到达点C时停止,运动时间为t秒,平移过程中,直线m与线段、分别交于点E、F .
(1)、求D点坐标和k的值;(2)、平行于x轴的直线m , 从原点O出发,以每秒1个单位长度的速度沿方向移动,到达点C时停止,运动时间为t秒,平移过程中,直线m与线段、分别交于点E、F .①记线段的长度为L , 当点F在点E右边时,求L与t的函数关系式;
②当四边形为平行四边形时,求t的值,并说明此时的平行四边形是否为菱形;
(3)、在(2)的情况下,以为边向下作等边(点P在线段下方),与重叠部分的面积记为S . 填空:当秒时,S的值;当E点落在中点时,S的值 .