2024年广东省数学八(下)期末复习:精选压轴题(1)
试卷更新日期:2024-06-02 类型:复习试卷
一、单选题
-
1. 如图,已知点 , 当直线与线段有交点时,k的取值范围是( )
 A、 B、或 C、 D、2. 如图,点A的坐标为 , 点B在直线上运动,当线段最短时,点B的坐标为( )
A、 B、或 C、 D、2. 如图,点A的坐标为 , 点B在直线上运动,当线段最短时,点B的坐标为( ) A、(0,0) B、 C、 D、3. 菱形在平面直角坐标系中的位置如图所示,点的坐标为 , , 则点的坐标为( )
A、(0,0) B、 C、 D、3. 菱形在平面直角坐标系中的位置如图所示,点的坐标为 , , 则点的坐标为( ) A、 B、 C、 D、4. 已知一次函数( , k是常数),则下列结论正确的是( )A、若点在一次函数的图象上,则它的图象与两个坐标轴围成的三角形面积是2; B、若 , 则一次函数图象上任意两点和满足: C、一次函数的图象不一定经过第三象限 D、若对于一次函数和 , 无论x取任何实数,总有 , 则k的取值范围是或5. 点P从某四边形的一个顶点A出发,沿着该四边形的边逆时针匀速运动一周.设点P运动的时间为x,点P与该四边形对角线交点的距离为y,表示y与x的函数关系的大致图像如图所示,则该四边形可能是( )
A、 B、 C、 D、4. 已知一次函数( , k是常数),则下列结论正确的是( )A、若点在一次函数的图象上,则它的图象与两个坐标轴围成的三角形面积是2; B、若 , 则一次函数图象上任意两点和满足: C、一次函数的图象不一定经过第三象限 D、若对于一次函数和 , 无论x取任何实数,总有 , 则k的取值范围是或5. 点P从某四边形的一个顶点A出发,沿着该四边形的边逆时针匀速运动一周.设点P运动的时间为x,点P与该四边形对角线交点的距离为y,表示y与x的函数关系的大致图像如图所示,则该四边形可能是( )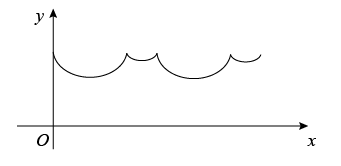 A、
A、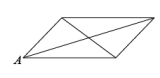 B、
B、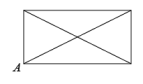 C、
C、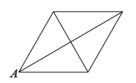 D、
D、 6. 如图,的平分线与邻补角的平分线相交于点 , 平分于点 , , , , 则的长度为.( )
6. 如图,的平分线与邻补角的平分线相交于点 , 平分于点 , , , , 则的长度为.( ) A、 B、 C、 D、7. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为.若 , 则的值是( )
A、 B、 C、 D、7. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNPQ的面积分别为.若 , 则的值是( ) A、30 B、20 C、18 D、108. 如图,矩形中,为的中点,过点的直线分别与 , 交于点 , , 连接交于点 , 连接 , . 若 , , 则下列结论:① , ;②;③四边形是菱形;④ . 其中正确结论的个数是( )
A、30 B、20 C、18 D、108. 如图,矩形中,为的中点,过点的直线分别与 , 交于点 , , 连接交于点 , 连接 , . 若 , , 则下列结论:① , ;②;③四边形是菱形;④ . 其中正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 如图,矩形对角线相交于点O,E为上一点,连接 , F为的中点,连接 , 若 , 则的长为 .
 10. 如图,在直角坐标系中,点A的坐标为 , 以线段为边在第四象限内作等边 , 点为x轴正半轴上一动点,连接 , 以线段为边在第四象限内作等边 , 直线交y轴于点E , 则四边形的面积是 . (结果用含a的式子表示)
10. 如图,在直角坐标系中,点A的坐标为 , 以线段为边在第四象限内作等边 , 点为x轴正半轴上一动点,连接 , 以线段为边在第四象限内作等边 , 直线交y轴于点E , 则四边形的面积是 . (结果用含a的式子表示) 11. 如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE,延长 EF 交 CD 于 G,接 CF,AG.下列结论:① AE∥FC;②∠EAG=45°,且BE+DG=EG;③ ;④ AD=3DG,正确的是(填序号).
11. 如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE,延长 EF 交 CD 于 G,接 CF,AG.下列结论:① AE∥FC;②∠EAG=45°,且BE+DG=EG;③ ;④ AD=3DG,正确的是(填序号).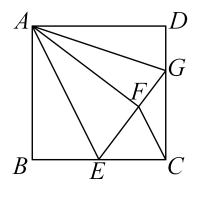 12. 如图,▱中, , , , 对角线 , 相交于点 , 过点的线段交于点 , 交于点 , 以下说法中:;;;的面积与的面积比为:其中,正确的序号有 .
12. 如图,▱中, , , , 对角线 , 相交于点 , 过点的线段交于点 , 交于点 , 以下说法中:;;;的面积与的面积比为:其中,正确的序号有 . 13. 如图,是内一点,分别是AB,AC,CD,BD的中点,则四边形EFGH的周长为.
13. 如图,是内一点,分别是AB,AC,CD,BD的中点,则四边形EFGH的周长为.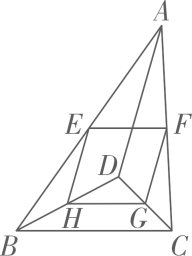 14. 编程兴趣小组为半径为0.2米的圆形扫地机器人编制了如图所示的程序,若扫地机器人在无障碍的实验室平地上按照编制的程序扫地,则这个扫地机器人扫过的实验室平地的面积是米 .
14. 编程兴趣小组为半径为0.2米的圆形扫地机器人编制了如图所示的程序,若扫地机器人在无障碍的实验室平地上按照编制的程序扫地,则这个扫地机器人扫过的实验室平地的面积是米 . 15. 如图,的两条直角边 , 分别以为边作正方形和正方形 . 点H是线段上一点,连接 , 作矩形 . 线段与交于点P,线段与交于点Q,连接线段和的中点M,N.和四边形的面积分别记为 , 和 . 给出下列四个结论:
15. 如图,的两条直角边 , 分别以为边作正方形和正方形 . 点H是线段上一点,连接 , 作矩形 . 线段与交于点P,线段与交于点Q,连接线段和的中点M,N.和四边形的面积分别记为 , 和 . 给出下列四个结论:①;②;③;④ .
其中正确的结论是 . (填写所有正确结论的序号)
 16. 如下图,三角形纸片ABC,点D是BC边上一点,连接AD,把沿着AD翻折,得到 , DE与AC交于点F.若点F是DE的中点, , 的面积为9,则点B、E之间的距离为 .
16. 如下图,三角形纸片ABC,点D是BC边上一点,连接AD,把沿着AD翻折,得到 , DE与AC交于点F.若点F是DE的中点, , 的面积为9,则点B、E之间的距离为 .
三、解答题
-
17. 如图1,在平面直角坐标系中,直线交轴于点 , 交轴于点 , 点坐标为 , 直线:与直线相交于点 , 点的横坐标为 .
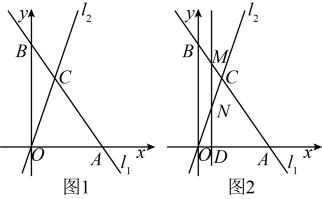 (1)、求直线的解析式;(2)、在轴上是否存在一点 , 使得是以为腰的等腰三角形?若存在,求出符合条件的点的坐标;若不存在,说明理由;(3)、如图2,点是轴上一动点,过点作轴的垂线,分别交、于点 , 当时,求点的坐标.18. 如图,在等腰中, , , 点D是直线上一动点,以为边,在下方作等边 .
(1)、求直线的解析式;(2)、在轴上是否存在一点 , 使得是以为腰的等腰三角形?若存在,求出符合条件的点的坐标;若不存在,说明理由;(3)、如图2,点是轴上一动点,过点作轴的垂线,分别交、于点 , 当时,求点的坐标.18. 如图,在等腰中, , , 点D是直线上一动点,以为边,在下方作等边 . (1)、直接写出的长,;(2)、当点D从点B运动到点C时,求点E的运动路径长;(3)、当时,求出的值.19. 已知在正方形中,
(1)、直接写出的长,;(2)、当点D从点B运动到点C时,求点E的运动路径长;(3)、当时,求出的值.19. 已知在正方形中, (1)、如图1,点、分别为、边上的动点,且 , 连接、交于点 , 点为正方形对角线的交点.
(1)、如图1,点、分别为、边上的动点,且 , 连接、交于点 , 点为正方形对角线的交点.①猜想线段与之间有怎样的数量和位置关系?请直接写出你的猜想,不需证明;
②下列结论:甲同学认为的值不变;乙同学认为:的值不变,其中只有一个结论正确,请选择正确的结论并求其值;
(2)、如图2,是等腰三角形, , 求证: .20. 如图,在平面直角坐标系中,四边形的顶点是 , , , , 点P是x轴上一动点,连接 . (1)、求直线的解析式;(2)、若 , 求点P的坐标;(3)、当点P在线段(点P不与点C重合)上运动时,设与线段相交于点D,以为边作平行四边形 , 连接 , 求的最小值.21. 如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连接PO并延长交BC于点Q,设运动时间为t(0<t<5).
(1)、求直线的解析式;(2)、若 , 求点P的坐标;(3)、当点P在线段(点P不与点C重合)上运动时,设与线段相交于点D,以为边作平行四边形 , 连接 , 求的最小值.21. 如图,在▱ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s.连接PO并延长交BC于点Q,设运动时间为t(0<t<5). (1)、当t为何值时,四边形ABQP是平行四边形?(2)、设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.22. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=-x+b与x轴交于点A,且经过定点B(-1,5),直线l1与l2交于点C(2,m).
(1)、当t为何值时,四边形ABQP是平行四边形?(2)、设四边形OQCD的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t,使点O在线段AP的垂直平分线上?若存在,求出t的值;若不存在,请说明理由.22. 如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=-x+b与x轴交于点A,且经过定点B(-1,5),直线l1与l2交于点C(2,m). (1)、求k、b和m的值;(2)、求△ADC的面积;(3)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;(4)、若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.23. 已知,在中, , 点为边上一点,连接 , 将线段绕点按顺时针方向旋转得到 , 连接 .
(1)、求k、b和m的值;(2)、求△ADC的面积;(3)、在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由;(4)、若动点P在线段DA上从点D开始以每秒1个单位的速度向点A运动,设点P的运动时间为t秒.是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.23. 已知,在中, , 点为边上一点,连接 , 将线段绕点按顺时针方向旋转得到 , 连接 . (1)、如图 , 当时,
(1)、如图 , 当时,①求证:;
②当的周长取最小值为时,求的周长;
(2)、如图 , 当 , 时,若 , 求的值.24. 【背景介绍】勾股定理是几何学中的明珠,充满着魅力,千百年来,人们对它的证明趋之若鹜,其中有著名的数学家,也有业余数学爱好者,向常春在1994年构造发现了一个新的证法.如图.
 (1)、【小试牛刀】
(1)、【小试牛刀】把两个全等的直角三角形如图1放置,其三边长分别为 , , . 显然, , . 请用 , , 分别表示出梯形 , 四边形 , 的面积,再探究这三个图形面积之间的关系,可得到勾股定理: , , , 则它们满足的关系式为 , 经化简,可得到勾股定理.
(2)、如图2,河道上 , 两点(看作直线上的两点)相距160米, , 为两个菜园(看作两个点), , , 垂足分别为 , , 米,米,现在菜农要在上确定一个抽水点 , 使得抽水点到两个菜园 , 的距离和最短,则该最短距离为米.(3)、【知识迁移】借助上面的思考过程,画图说明并求代数式的最小值 .
25. 在□ABCD中,点O是对角线BD的中点,点E在边BC上,EO的延长线与边AD交于点F , 连接BF、DE如图1. (1)、求证:四边形BEDF是平行四边形;(2)、若DE=DC , ∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、P如图2.
(1)、求证:四边形BEDF是平行四边形;(2)、若DE=DC , ∠CBD=45°,过点C作DE的垂线,与DE、BD、BF分别交于点G、H、P如图2.①当CD=6.CE=4时,求BE的长;
②求证:CD=CH .
26. 如图,平面直角坐标系中,直线与x轴交于点A(6,0),与y轴交于点B,与直线y=2x交于点C(a,4). (1)、求点C的坐标及直线AB的表达式;(2)、如图,在x轴上有一点E,过点E作直线轴,交直线y=2x于点F,交直线于点G,若GF的长为3.求点E的坐标;(3)、在轴上是否存在一点 , 使以为顶点的三角形是等腰三角形,若存在,直接写出点的坐标;若不存在,说明理由.
(1)、求点C的坐标及直线AB的表达式;(2)、如图,在x轴上有一点E,过点E作直线轴,交直线y=2x于点F,交直线于点G,若GF的长为3.求点E的坐标;(3)、在轴上是否存在一点 , 使以为顶点的三角形是等腰三角形,若存在,直接写出点的坐标;若不存在,说明理由.