2024年广东省数学七（下）期末复习：精选压轴题（3）

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，点D、E分别是 $△ A B C$ 边 $B C$ 、 $A C$ 上一点， $B D = 2 C D$ ， $A E = C E$ ，连接 $A D 、 B E$ 交于点F，若 $△ A B C$ 的面积为12，则 $△ B D F$ 与 $△ A E F$ 的面积之差 $S_{△ B D F} - S_{△ A E F}$ 等于（）

A、1 B、2 C、3 D、4

查看试题解析
2. 如图，在 $△ A B C$ 中，以点 $B$ 为圆心， $A B$ 为半径画弧交 $B C$ 于点 $D$ ，以点 $C$ 为圆心， $A C$ 为半径画弧交 $B C$ 于点 $E$ ，连接 $A E$ ， $A D$ ．设 $∠ A C B = α$ ， $∠ E A D = β$ ，则 $∠ B$ 的度数为（）

A、 $2 β - α$ B、 $α - \frac{1}{2} β$ C、 $2 α - β$ D、 $α + \frac{1}{2} β$

查看试题解析
3. 有一列数按如下规律排列： $- \frac{\sqrt{2}}{2}$ ， $\frac{\sqrt{3}}{4}$ ， $- \frac{1}{4}$ ， $\frac{\sqrt{5}}{16}$ ， $- \frac{\sqrt{6}}{32}$ ， $\frac{\sqrt{7}}{64}$ …则第10个数是（）

A、 $- \frac{\sqrt{10}}{2^{9}}$ B、 $\frac{\sqrt{10}}{2^{9}}$ C、 $- \frac{\sqrt{11}}{2^{10}}$ D、 $\frac{\sqrt{11}}{2^{10}}$

查看试题解析
4. 人的大脑所能记忆的内容是有限的，随着时间的推移，记忆的东西会逐渐被遗忘．德国心理学家艾宾浩斯（Hermann Ebbinghaus ， 1850－1909）第一个发现了记忆遗忘规律，他根据自己得到的测试数据描绘了一条曲线（如图所示），这就是非常有名的艾宾浩斯遗忘曲线，其中竖轴表示学习中的记忆保持量，横轴表示时间，分析图象得到下列结论，其中正确的是（）

A、记忆后0~2小时比2~4小时的遗忘速度慢 B、记忆保持量下降到 $50 %$ 所用时间为4小时 C、点A表示记忆15小时后记忆保持量约为36% D、记忆16小时后，记忆保持量始终保持不变

查看试题解析
5. 如图，数学兴趣小组在综合与实践课上用一张边长为 $8 c m$ 的正方形纸片先制作了一幅如图1所示的七巧板，再拼成如图2所示的作品，则图2中①和②的面积之和是（）

A、 $12 c m^{2}$ B、 $14 c m^{2}$ C、 $16 c m^{2}$ D、 $18 c m^{2}$

查看试题解析
6. 阅读理解：我们把 $| \begin{array}{l} a b \\ c d \end{array} |$ 称作二阶行列式，规定它的运算法则为 $| \begin{array}{l} a b \\ c d \end{array} |$ ＝ad-bc，例如 $| \begin{array}{l} 13 \\ 24 \end{array} |$ ＝1×4-2×3＝-2，如果 $| \begin{array}{l} 2 \\ 1 \end{array} \begin{array}{l} 3 - x \\ x \end{array} |$ ＞0，则x的取值范围是（）

A、x＞1 B、x＜-1 C、x＞3 D、x＜-3

查看试题解析

二、填空题

7. 如图，在 $△ A B C$ ， $∠ C = 90 °$ ， $B C = 8 c m$ ， $A C = 6 c m$ ， $A E$ 是 $△ A B C$ 的中线，动点P从点A出发，以每秒 $3 c m$ 的速度沿 $A \to C \to E$ 运动，最终到达点E．当点P运动s时， $△ A P E$ 的面积等于 $9 c m^{2}$ ．

查看试题解析
8. 如图，已知 $A B ∥ C D$ ，点 $M$ ， $N$ 分别在直线 $A B$ 、 $C D$ 上， $∠ M E N = 90 °$ ， $∠ C N E = ∠ E N F$ ，则 $∠ α$ 与 $∠ β$ 的数量关系．

查看试题解析
9. 对于实数a，b，c，d，定义 $| \begin{array}{l} a & c \\ b & d \end{array} | = a d - b c$ ，已知 $- 2 < | \begin{array}{l} 2 & 4 \\ 3 & x \end{array} | \leq 4$ ，则x的取值范围是.

查看试题解析
10. 如图，四边形 $A B C D 、 C E F G$ 均为正方形，其中正方形 $A B C D$ 面积为 $8 c m^{2}$ ．图中阴影部分面积为 $5 c m^{2}$ ，正方形 $C E F G$ 面积为．

查看试题解析
11. 如图，在平面直角坐标系中，已知正方形 $A B C D$ 的边长为8，与y轴交于点 $M (0 ， 5)$ ，顶点 $C (6 ， - 3)$ ，将一条长为2023个单位长度且没有弹性的细绳一端固定在点M处，从点M出发将细绳紧绕在正方形 $A B C D$ 的边上，则细绳的另一端到达的位置点N的坐标为．

查看试题解析
12. 如图， $△ A B C$ 中，点D、E分别是 $A B$ 、 $B C$ 的中点，连接 $A E$ 、 $C D$ 交于点F ．当 $△ A F D$ 的面积为 $\frac{7}{2}$ 时， $△ A B C$ 的面积为．

查看试题解析
13. 如图，在单位为1的方格纸上， $△ A A_{1} A_{2}$ ， $△ A_{2} A_{3} A_{4}$ ， $△ A_{4} A_{5} A_{6}$ ， …，都是斜边在x轴上，斜边长分别为2，4，6，8，10，…的等腰直角三角形，若 $△ A A_{1} A_{2}$ 的顶点坐标分别为 $A (1 ， 0)$ ， $A_{1} (0 ， 1)$ ， $A_{2} (- 1 ， 0)$ ．则依图中所示规律， $A_{2024}$ 的坐标为．

查看试题解析

三、解答题

14. 对 $x$ ， $y$ 定义一种新运算 $T$ ，规定： $T (x ， y) = \frac{a x + b y}{x + y}$ （其中 $a$ ， $b$ 均为非零常数），这里等式右边是通常的四则运算，例如： $T (0 ， 1) = \frac{a \times 0 + b \times 1}{0 + 1} = b$ ，已知 $T (1 ， 1) = 2.5$ ， $T (4 ， - 2) = 4$ ．

(1)、求 $a$ ， $b$ 的值；

(2)、若关于 $m$ 的不等式组 ${\begin{array}{l} \begin{array}{l} T (4 m ， 5 - 4 m) \leq 3 \end{array} \\ T (2 m ， 3 - 2 m) ＞ P \end{array}$ 恰好有2个整数解，求实数 $P$ 的取值范围．

查看试题解析
15. 如图1，在平面直角坐标系中，点 $A (a ， 0)$ ， $B (b ， 0)$ ， $C (- 1 ， 2)$ ，且a、b满足 $| 2 a + b + 1 | + {(a + 2 b - 4)}^{2} = 0$ ．

(1)、求a ， b的值；

(2)、在x轴上存在一点M ，使 $S_{△ C O M} = \frac{1}{2} S_{△ A B C}$ ，求出点M的坐标；

(3)、如图2，过点C作 $C D ⊥ y$ 轴交y轴于点D ，点P为线段 $C D$ 延长线上一动点，连接 $O P$ ， $O E$ 平分 $∠ A O P$ ， $O F ⊥ O E$ ．当点P运动时， $\frac{∠ O P D}{∠ D O E}$ 的值是否会改变？若不变，求其值；若改变，说明理由．

查看试题解析
16. 阅读下面的文字，解答问题∶大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来．将这个数减去其整数部分，得到的差就是小数部分，因为 $\sqrt{2}$ 的整数部分是1，于是用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分．又例如：
∵ $\sqrt{4} < \sqrt{7} < \sqrt{9}$ ，即 $2 < \sqrt{7} < 3$ ，
∴ $\sqrt{7}$ 的整数部分是2，小数部分为 $\sqrt{7} - 2$ ．
根据上述材料，回答下列问题：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是．

(2)、 $6 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 6 + \sqrt{3} < b$ ，求 $a + b$ 的值；

(3)、若 $\sqrt{11}$ 的整数部分为x ，小数部分为y，求 ${(y - \sqrt{11})}^{x - 1}$ 的平方根．

查看试题解析
17. 如图，已知 $A B ∥ C D$ ，点 $E$ ， $F$ 分别在 $A B$ ， $C D$ 上，点 $O$ 在 $A B$ ， $C D$ 之间， $O$ ， $B$ ， $D$ 三点均在直线 $E F$ 的同侧．

(1)、如图 $1$ ，试说明 $∠ E O F = ∠ B E O + ∠ D F O$ ；

(2)、如图 $2$ ，若 $O E ⊥ O F$ ， $E G$ ， $F G$ 分别平分 $∠ B E O$ 和 $∠ D F O$ ，求 $∠ G$ 的度数；

(3)、如图 $3$ ，若 $∠ E O F$ 的度数为 $α$ ， $E M$ 平分 $∠ B E O$ 交 $F O$ 的延长线于点 $M$ ， $F N$ 平分 $∠ D F O$ 交 $E O$ 的延长线于点 $N$ ，请用含 $α$ 的代数式表示 $∠ M + ∠ N$ ．

查看试题解析
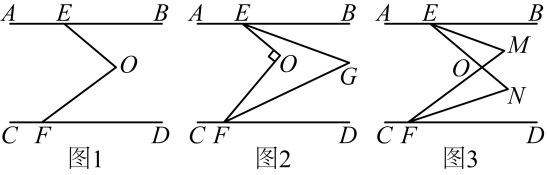18. 如图，AE与BD相交于点C，AC＝EC，BC＝DC，AB＝4cm，点P从点A出发，沿A→B→A方向以3cm/s的速度运动，点Q从点D出发，沿D→E方向以1cm/s的速度运动，P、Q两点同时出发．当点P到达点A时，P、Q两点同时停止运动．设点P的运动时间为t（s）．

(1)、求证：AB $/ /$ DE．

(2)、写出线段AP的长（用含t的式子表示）．

(3)、连结PQ，当线段PQ经过点C时，求t的值．

查看试题解析
19. 如图，在平面直角坐标系 $x O y$ 中，点 $A (a ， 0) ， B (c ， c) ， C (0 ， c)$ ，且满足 ${(a + 8)}^{2} + \sqrt{c + 4} = 0$ ， $P$ 点从 $A$ 点出发沿 $x$ 轴正方向以每秒2个单位长度的速度匀速移动， $Q$ 点从 $O$ 点出发沿 $y$ 轴负方向以每秒1个单位长度的速度匀速移动．

(1)、直接写出点 $B$ 的坐标， $A O$ 和 $B C$ 位置关系是 ▲ ；

(2)、如图（1）当 $P 、 Q$ 分别在线段 $A O ， O C$ 上时，连接 $P B$ ， $Q B$ ，使 $S_{△ P A B} = 4 S_{△ Q B C}$ ，求出点 $P$ 的坐标；

(3)、在 $P 、 Q$ 的运动过程中，当 $∠ C B Q = 30 °$ 时，请直接写出 $∠ O P Q$ 和 $∠ P Q B$ 的数量关系．

查看试题解析
20. 如图1，在平面直角坐标系中， $A (a ， 0)$ ， $C (b ， 2)$ ，且满足 $\sqrt{a + 2} + {(b - 2)}^{2} = 0$ ，过C作 $C B ⊥ x$ 轴于B．

(1)、求△ABC的面积；

(2)、若过B作 $B D ∥ A C$ 交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数；

(3)、在y轴上存在点P使得△ABC和△ACP的面积相等，请直接写出P点坐标．

查看试题解析
21. 阅读理解，自主探究：
“一线三垂直”模型是“一线三等角”模型的特殊情况，即三个等角角度为90°，于是有三组边相互垂直．所以称为“一线三垂直模型”．当模型中有一组对应边长相等时，则模型中必定存在全等三角形．

(1)、问题解决：如图1，在等腰直角 $△ A B C$ 中， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，过点C作直线 $D E$ ， $A D ⊥ D E$ 于D， $B E ⊥ D E$ 于E，求证： $△ A D C ≌ △ C E B$ ；

(2)、问题探究：如图2，在等腰直角 $△ A B C$ 中， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，过点C作直线 $C E$ ， $A D ⊥ C E$ 于D， $B E ⊥ C E$ 于E， $A D ＝ 2.5$ cm， $D E ＝ 1.7$ cm，求 $B E$ 的长；

(3)、拓展延伸：如图3，在平面直角坐标系中， $A （ - 1 ， 0 ）， C （ 1 ， 3 ）$ ， $△ A B C$ 为等腰直角三角形， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，求B点坐标．

查看试题解析
22. 在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，直线l经过点A ，过点B、C分别作l的垂线，垂足分别为点D、E ．

(1)、【特例体验】
如图1，若直线 $l ∥ B C$ ， $B D = 1$ ，则线段 $D E$ 的长为．

(2)、【探究应用】
如图2，若直线l从图1状态开始绕点A顺时针旋转 $α (0 ° < α < 45 °)$ 时，线段 $B D$ 、 $C E$ 和 $D E$ 的数量关系是；

(3)、如图3，若直线l从图1状态开始绕点A顺时针旋转 $α (45 ° < α < 90 °)$ 时与线段 $B C$ 相交，探究线段 $B D$ 、 $C E$ 和 $D E$ 的数量关系并说明理由

(4)、若 $B D = a$ ， $C E = b$ （a ， b均为正数），请你直接写出以点B、D、C、E为顶点的四边形的面积．

查看试题解析
23. 在 $△ A B C$ 中， $C D$ 平分 $∠ A C B$ 交 $A B$ 于点D ．

(1)、如图1， $D M ⊥ A C ， D N ⊥ B C$ ，垂足分别为M ， N ．试说明： $C M = C N$ ；

(2)、如图2，点E是线段 $B D$ 上一点，过点E作 $E F ∥ B C$ 交 $A C$ 于点F ，与 $C D$ 交于点H ， $E G$ 平分 $∠ A E F$ 交 $C D$ 于点G；
①若 $∠ A C B = 100 ° ， ∠ B = 30 °$ ，则 $∠ C G E =$ ▲ ；
②若 $∠ A = 40 °$ ，则 $∠ C G E =$ ▲ ；
③探究 $∠ C G E$ 与 $∠ A$ 之间的数量关系，并说明理由．

查看试题解析
24. 在直角坐标系中，有正方形 $A B C D$ （四条边相等，四个内角都是 $90 °$ ），其中 $A B$ 平行于y轴，点 $A$ 在第二象限．

(1)、如图，若 $A (- 2 ， 4)$ ， $A B$ 长为6，则点B ， C ， D的坐标分别为：B ， C ， D；

(2)、若 $A (- 3 ， a)$ ， $B (- 3 ， b)$ ，点是直角坐标系中的一个动点， $P (c ， \frac{2}{3} a)$ ，点Q从B出发，以每秒1个单位长度的速度沿射线BC方向运动，运动时间为t秒，若 $\sqrt{a - 3} + {(b + 2)}^{2} + | c + t - 3 | = 0$ ．
①当 $t = 2$ 时，求 $△ A P Q$ 的面积；

②试问是否存在点P ，使得 $S_{△ A P Q} = \frac{1}{2} S_{△ A P B}$ ，若存在，请求出P点的坐标；若不存在，请说明理由．

查看试题解析
25. 甲同学在学完《相交线与平行线》后，想通过折铁丝的方式进一步探索相交线与平行线的知识，他的具体操作步骤如下：
第一步：将一根铁丝 $A B$ 在 $C$ ， $D$ ， $E$ 处弯折得到如下图①的形状，其中 $A C ∥ D E$ ， $C D ∥ B E$ ．
第二步：将 $D E$ 绕点D旋转一定角度，再将 $B E$ 绕点E旋转一定角度并在 $B E$ 上某点 $F$ 处弯折，得到如下图②的形状．
第三步：再拿出另外一根铁丝弯折成 $∠ G$ ，跟前面弯折的铁丝叠放成如下图③的形状．
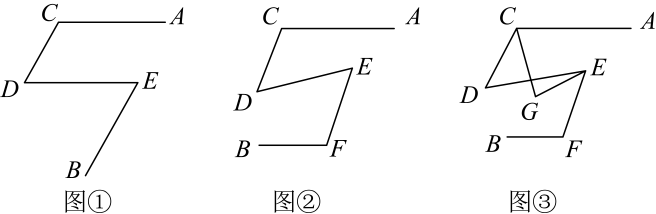
请根据上面的操作步骤，解答下列问题：

(1)、如图①，若 $∠ C = 2 ∠ D$ ，求 $∠ E$ ；

(2)、如图②，若 $A C ∥ B F$ ，请判断 $∠ C$ ， $∠ D$ ， $∠ E$ ， $∠ F$ 之间的数量关系，并说明理由；

(3)、在（2）的条件下，如图③，若 $∠ A C D = 3 ∠ D C G$ ， $∠ D E F = 3 ∠ D E G$ ，设 $∠ D = x$ ， $∠ F = y$ ，求 $∠ G$ ．（用含 $x$ ， $y$ 的式子表示）

查看试题解析
26. 如图，以直角 $△ A O C$ 的直角顶点O为原点，以 $O C ， O A$ 所在直线为x轴和y轴建立平面直角坐标系，点 $A （ 0 ， a ）， C （ b ， 0 ）$ 满足 $\sqrt{a - b + 2} + | b - 8 | = 0$ ，

(1)、点A的坐标为；点C的坐标为．

(2)、已知坐标轴上有两动点 $P ， Q$ 同时出发，P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动，Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动，点P到达O点整个运动随之结束． $A C$ 的中点D的坐标是 $(4 ， 3)$ ，设运动时间为t秒．问：是否存在这样的t，使得 $△ O D P$ 与 $△ O D Q$ 的面积相等？若存在，请求出t的值；若不存在，请说明理由．

(3)、在（2）的条件下，若 $∠ D O C ＝ ∠ D C O ，$ 点G是第二象限中一点，并且y轴平分 $∠ G O D$ ．点E是线段 $O A$ 上一动点，连接 $C E$ 交 $O D$ 于点H，当点E在线段 $O A$ 上运动的过程中，探究 $∠ G O A ， ∠ O H C ， ∠ A C E$ 之间的数量关系，并证明你的结论（三角形的内角和为180°可以直接使用）．

查看试题解析