2024年广东省数学七（下）期末复习：精选压轴题（2）

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，动点 $P$ 在平面直角坐标系中按图中所示方向运动，第一次从原点 $O$ 运动到点 $P_{1} (1 ， 1)$ ，第二次运动到点 $P_{2} (2 ， 1)$ ，第三次运动到点 $P_{3} (3 ， 0)$ ，第四次运动到点 $P_{4} (4 ， - 2)$ ，第五次运动到点 $P_{5} (5 ， 0)$ ，第六次运动到点 $P_{6} (6 ， 2)$ ，按这样的运动规律，点 $P_{2023}$ 的纵坐标是（）

A、 $- 2$ B、 $0$ C、 $1$ D、 $2$

查看试题解析
2. 已知方程组 ${\begin{array}{l} x + y = 1 - a ， \\ x - y = 3 a + 5 \end{array}$ 的解x为正数，y为非负数，给出下列结论：① $- 1 < a \leq 1$ ；②当 $a = - \frac{5}{3}$ 时， $x = y$ ；③当 $a = - 2$ 时，方程组的解也是方程 $x + y = 5 + a$ 的解；④若 $0 < x \leq 1$ ，则 $2 \leq y < 4$ .其中正确的是（）

A、①② B、②③ C、①④ D、②③④

查看试题解析
3. 如图，在△ABC中，BD平分∠ABC，E是BC的中点，过点E作BC的垂线交BD于点F，连结CF。若∠A=50°，∠ACF=40°，则∠CFD的度数为（）

A、30° B、45° C、55° D、60°

查看试题解析
4. 一个寻宝游戏通道如图所示，通道在同一平面内由AB、BC、CD、DA、AC、BD组成．定位仪器放置在BC的中点M处，设寻宝者行进时间为x，寻宝者与定位仪器之间的距离为y，寻宝者匀速前进，y与x的函数关系图象如图所示，则寻宝者的行进路线可能是（）

A、A→B→O B、A→D→O C、A→O→D D、B→O→C

查看试题解析
5. 如图，在△ABC中，AB＝AC，按如下步骤作图：以点A为圆心、适当长度为半径作弧，分别交AB、AC于点M、N；分别以点M、N为圆心、大于 $\frac{1}{2}$ MN的长为半径作弧，两弧相交于点F，连接AF并延长，交BC于点E．下列结论不一定成立的是（）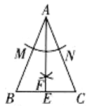

A、∠ABC＝∠ACB B、BE＝CE C、AE⊥BC D、∠BAE＝ $\frac{1}{2}$ ∠B

查看试题解析
6. 如图， $A B ∥ C D$ ，将一副直角三角板作如下摆放， $∠ G E F = 60 °$ ， $∠ M N P = 45 °$ ．下列结论：① $G E ∥ M P$ ；② $∠ E F N = 150 °$ ；③ $∠ B E F = 75 °$ ；④ $∠ A E G = ∠ P M N$ ．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 定义新运算 $a ⊙ b = b (a < b)$ ，若 $\frac{1 - 2 x}{3} ⊙ 7 = 7$ ，则x的取值范围是（）

A、 $x > - 10$ B、 $x > - 11$ C、 $x < - 10$ D、 $x < 11$

查看试题解析

二、填空题

8. 如图，线段 $O B$ 、 $O C$ 、 $O A$ 的长度分别是 $1$ 、 $2$ 、 $3$ ，且 $O C$ 平分 $∠ A O B .$ 若将 $A$ 点表示为 $(3 ， 30 °)$ ， $B$ 点表示为 $(1 ， 120 °)$ ，则 $C$ 点可表示为．

查看试题解析
9. 如图，在平面直角坐标系中，有若干个横纵坐标分别为整数的点，其顺序为 $(1 ， 0)$ 、 $(2 ， 0)$ 、 $(2 ， 1)$ 、 $(1 ， 1)$ 、 $(1 ， 2)$ 、 $(2 ， 2)$ …根据这个规律，第2023个点的坐标．

查看试题解析
10. 如图，四边形 $A B C D 、 C E F G$ 均为正方形，其中正方形 $A B C D$ 面积为 $8 c m^{2}$ ．图中阴影部分面积为 $5 c m^{2}$ ，正方形 $C E F G$ 面积为．

查看试题解析
11. 如图，在△ABC中，AB＝AC＝10cm，BC＝8cm，AB的垂直平分线交AB于点M，交AC于点N，在直线MN上存在一点P，使P、B、C三点构成的△PBC的周长最小，则△PBC的周长最小值为．

查看试题解析
12. 如图， $A B ∥ C D$ ， $∠ C = 60 °$ ，点 $E$ 是射线 $C D$ 上一点，连接 $A E$ ，将 $△ A E C$ 沿着 $A E$ 翻折得 $△ A E F$ ，点 $C$ 的对应点为点 $F$ ，若 $∠ E A F = 2 ∠ F A B$ ，那么 $∠ A E C =$ ．

查看试题解析
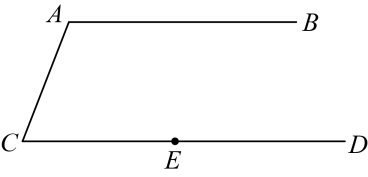13. 如图，在平面直角坐标系中，动点P按图中箭头所示方向从原点出发，第1次运动到点 $P_{1} (1 ， 1)$ ，第2次接着运动到点 $P_{2} (2 ， 0)$ ，第3次接着运动到点 $P_{3} (3 ， - 2)$ ， …，按这样的运动规律，点 $P_{2023}$ 的坐标是．

查看试题解析
14. 已知关于x ， y的二元一次方程 $(m - 2) x + (m - 3) y + 2 m - 3 = 0$ ，当m每取一个值时，就有一个方程，而这些方程有一个公共解，这个公共解是．

查看试题解析
15. 如图，在平面直角坐标系中有一个点 $A (1 ， 0)$ ，点 $A$ 第一次向左跳动至 $A_{1} (- 1 ， 1)$ ，第二次向右跳动至 $A_{2} (2 ， 1)$ ，第三次向左跳动至 $A_{3} (- 2 ， 2)$ ，第四次向右跳动至 $A_{4} (3 ， 2)$ ， …，依照此规律跳动下去，点 $A$ 第2023次跳动到点 $A_{2023}$ 的坐标为

查看试题解析

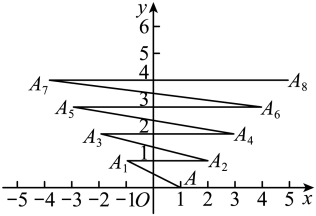
三、解答题

16. 有公共顶点的等腰直角三角形 $A C B$ 与等腰直角三角形 $A D E$ 按如图①所示放置， $∠ B A C = ∠ D A E = 90 °$ ， $A B = A C$ ， $A D = A E$ ，点 $D$ 在 $A C$ 上，点 $E$ 在 $B A$ 的延长线上．连接 $B D$ ， $C E$ ．

(1)、【观察猜想】
$B D$ 与 $C E$ 之间的数量关系是；位置关系是．

(2)、【探究证明】
将等腰直角三角形 $A D E$ 绕点 $A$ 逆时针旋转，如图②所示，使点 $C$ ， $D$ ， $E$ 在同一条直线上，连接 $B D$ ，交 $A C$ 于点 $H$ ． $B D$ 与 $C E$ 之间的关系是否仍然成立？请说明理由

查看试题解析
17. 如图①，直线 $A B ∥ C D$ ，直线 $E F$ 与 $A B ， C D$ 分别交于点G ， H ， $∠ E H D = α (0 ° < α < 90 °)$ ．将一个含 $30 °$ 角的直角三角板 $P M N$ 放置图中，使点N ， M分别在直线 $A B ， C D$ 上， $∠ P = 90 °$ ， $∠ P M N = 60 °$ ．

(1)、填空： $∠ P N B + ∠ P M D$ $∠ P$ （填“ $>$ ”“ $<$ ”或“ $=$ ”）；

(2)、 $P M ∥ E F$ ， $∠ M N G$ 的平分线 $N O$ 交直线 $C D$ 于点O ．
①如图②，当 $N O ∥ E F$ 时，求 $α$ 的度数；

②将三角板 $P M N$ 向左平移，用含 $α$ 的式子表示 $∠ M O N$ 的度数．

查看试题解析
18. 如图，已知格线相互平行，小明在格线中作 $∠ A O B$ 、 $∠ C P D$ 、 $∠ E Q F$ ，探究角的两边与格线形成的锐角所满足的数量关系．

(1)、如图 $1$ ， $∠ A O B = 60 °$ ，点 $O$ 在一条格线上，当 $∠ 1 = 20 °$ 时，求 $∠ 2$ 的度数；

(2)、如图 $2$ ， $∠ C P D = 60 °$ ，点 $P$ 在两条格线之间，用等式表示 $∠ 3$ 与 $∠ 4$ 的数量关系，并证明；

(3)、如图 $3$ ， $∠ E Q F = 60 °$ ，小明在图 $3$ 中作射线 $Q G$ ，使得 $∠ G Q F = 45 ° .$ 记 $Q G$ 与图中一条格线形成的锐角为 $α$ ， $Q E$ 与图中另一条格线形成的锐角为 $β$ ，探究 $α$ 与 $β$ 的数量关系，并用等式表示 $α$ 与 $β$ 的数量关系．

查看试题解析
19. 如图，点A的坐标为 $(1 ， 0)$ ，点B在y轴上，将三角形OAB沿x轴负方向平移，平移后的图形为三角形DEC，且点C的坐标为 $(- 3 ， 2)$ ．

(1)、点E的坐标为；点B的坐标为；

(2)、在四边形ABCD中，点P从点B出发，沿“ $B C \to C D$ ”移动．
①当点P在CD上时﹐设 $∠ C B P = x ， ∠ P A D = y ， ∠ B P A = z$ ，试用含x，y的式子表示z，写出解答过程．

②当点P在BC上﹐且直线OP平分四边形ABCD的面积时﹐求点P的坐标．

查看试题解析
20. 直线在同一平面内有平行和相交两种位置关系，线段首尾连接可以变换出很多不同的图形，这些不同的角又有很多不同关系，今天我们就来探究一下这些奇妙的图形吧！
【问题探究】

(1)、①如图1，若 $A B ∥ C D$ ，点P在 $A B ， C D$ 内部， $∠ B = 55 ° ， ∠ D = 30 °$ ，则 $∠ B P D =$ ；
②如图2，若 $A B ∥ C D$ ，将点P在 $A B ， C D$ 外部，求 $∠ B P D ， ∠ B ， ∠ D$ 之间数量关系（不需证明）；
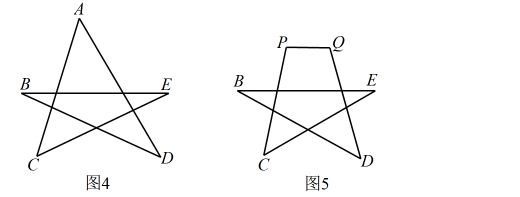
③如图3，写出 $∠ B P D ， ∠ B ， ∠ D ， ∠ B Q D$ 之间的数量关系：（不需证明）．

(2)、如图4，五角星 $A B C D E$ ，请直接写出 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E =$ ．

(3)、如图5，将五角星 $A B C D E$ 去掉一个角后， $∠ B ＋ ∠ C + ∠ D + ∠ E + ∠ P + ∠ Q$ 是多少？请证明你的结论．

查看试题解析
21. 问题解决：

(1)、问题情境：如图1所示，要在街道旁修建一个奶站，向居民区A、B提供牛奶，奶站应建在什么地方，才能使从A、B到P的距离之和最短？请画出点P的位置；

(2)、问题理解：如图2，在△ABC中，AB＝AC，AD平分∠BAC，点E是AC边的中点，点P是线段AD上的动点，画出PC＋PE取得最小值时点P的位置；

(3)、问题运用：如图3，在△ABC中，AB＝AC＝13，BC＝10，AD＝12，AD是∠BAC的平分线，当点E、P分别是AC和AD上的动点时，求PC＋PE的最小值．

查看试题解析
22. 如图1，在边长为 $10 c m$ 的正方形 $A B C D$ 中，点P从点A出发，沿A→B→C→D路线运动，到点D停止；点Q从点D出发，沿D→C→B→A路线运动，到点A停止．若点P、点Q同时出发，点P的速度为每秒 $1 c m$ ，点Q的速度为每秒 $2 c m$ ， a秒时点P、点Q同时改变速度，点P的速度为每秒 $2 c m$ ，点Q的速度为每秒 $1 c m$ ，图2是点P出发x秒后 $△ A P D$ 的面积 $S (c m^{2})$ 与 $x (s)$ 关系的图象．

(1)、根据图象得 $a =$ ；

(2)、设点P已行的路程为 $y_{1} (c m)$ ，点Q还剩的路程为 $y_{2} (c m)$ ，试分别求出改变速度后，y₁ ， y₂和出发后的运动时间x（秒）的关系式；

(3)、若点P、点Q在运动路线上相距的路程为 $18 c m$ ，求x的值．

查看试题解析
23. 如图

(1)、【感知】如图1， $A B ∥ C D$ ， ∠AEP＝50°，∠PFD＝120°，求∠EPF的度数；

(2)、【探究】如图2， $A B ∥ C D$ ， ∠AEP＝48°，∠PFC＝122°，求∠EPF的度数；

(3)、【应用】如图3，在以上【探究】条件下，∠PEA的平分线和∠PFC的平分线交于点G，求∠G的度数．

查看试题解析
24. 在平面直角坐标系中，已知点 $A (m ， 0)$ 、 $B (n ， 4)$ 、 $C (5 ， 0)$ ，且满足 $| m + n | + {(m - n + 8)}^{2} = 0$ ，线段 $A B$ 交y轴于点F，点D是y轴正半轴上的一点．

(1)、求出点A、B的坐标；

(2)、如图1，若 $D B ∥ A C$ ， $∠ B A C = α$ ，且 $A M$ 、 $D M$ 别平分 $∠ C A B$ ， $∠ O D B$ ，求 $∠ A M D$ 的度数（用含 $α$ 的代数式表示）；

(3)、如图2，坐标轴上是否存在一点P，使得 $△ A B P$ 面积和 $△ A B C$ 面积相等？若存在，求出P点的坐标；若不存在，请说明理由．

查看试题解析