2024年广东省数学七(下)期末复习:精选压轴题(1)
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的处接住她后用力一推,爸爸在处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和.爸爸在处接住小丽时,小丽距离地面的高度是( )
 A、1m B、1.6m C、 D、2. 如图,在△ABC中,以点B为圆心,AB为半径画弧交BC于点D , 以点C为圆心,AC为半径画弧交BC于点E , 连接AE , AD . 设∠ACB=α,∠EAD=β,则∠B的度数为( )
A、1m B、1.6m C、 D、2. 如图,在△ABC中,以点B为圆心,AB为半径画弧交BC于点D , 以点C为圆心,AC为半径画弧交BC于点E , 连接AE , AD . 设∠ACB=α,∠EAD=β,则∠B的度数为( ) A、2β-α B、α-β C、2α-β D、α+β3. 如图,一个机器人从点O出发,向正西方向走到达点;再向正北方向走到达点;再向正东方向走到达点;再向正南方向走到达点;再向正西方向走到达点 , 按如此规律走下去,当机器人走到点时,点的坐标为( )
A、2β-α B、α-β C、2α-β D、α+β3. 如图,一个机器人从点O出发,向正西方向走到达点;再向正北方向走到达点;再向正东方向走到达点;再向正南方向走到达点;再向正西方向走到达点 , 按如此规律走下去,当机器人走到点时,点的坐标为( )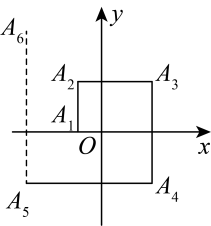 A、 B、 C、 D、4. 如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”,若 , , , 则的度数为( )
A、 B、 C、 D、4. 如图是小海为学校即将举办的“首届数学核心素养展示大赛”制作宣传海报时设计的艺术数字“1”,若 , , , 则的度数为( ) A、 B、 C、 D、5. 如图,长为 , 宽为的大长方形被分割为小块,除阴影 , 外,其余块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的有( )
A、 B、 C、 D、5. 如图,长为 , 宽为的大长方形被分割为小块,除阴影 , 外,其余块是形状、大小完全相同的小长方形,其较短的边长为 , 下列说法中正确的有( )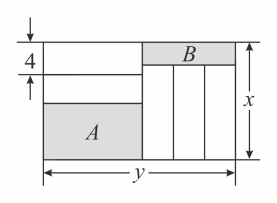
小长方形的较长边为;
阴影的较短边和阴影的较短边之和为;
若为定值,则阴影和阴影的周长和为定值;
当时,阴影和阴影的面积和为定值.
A、个 B、个 C、个 D、个6. 如图,已知与都是等边三角形,点B,C,D在同一条直线上,与相交于点 , 与相交于点 , 与相交于点 , 则下列结论:①;②;③;④是等边三角形,其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
7. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则.
 8. 如图,在中,将对折,使和在同一直线上,折痕为 , 延长至点D,使得 , 连接 , 若 , 则 .
8. 如图,在中,将对折,使和在同一直线上,折痕为 , 延长至点D,使得 , 连接 , 若 , 则 . 9. 下表中给出的每一对x , y的值都是二元一次方程的解,则不等式组的解集为 .
9. 下表中给出的每一对x , y的值都是二元一次方程的解,则不等式组的解集为 .1
2
3
3
1
10. 如图,正方形 , (每个正方形的顶点从第三象限开始,按顺时针方向,依次记为正方形的中心均在坐标原点处,各边均与轴或轴平行,若它们的边长依次是 , 则顶点的坐标为.
 11. 如图,在长方形中, , , 延长到点 , 使 , 连接 , 动点从点出发,以每秒2个单位的速度沿向终点运动,设点的运动时间为秒,当的值为秒时,和全等.
11. 如图,在长方形中, , , 延长到点 , 使 , 连接 , 动点从点出发,以每秒2个单位的速度沿向终点运动,设点的运动时间为秒,当的值为秒时,和全等. 12. 如图,用大小相同的小正方形拼图,第个图是一个小正方形;第个图由个小正方形拼成;第个图由个小正方形拼成,依此规律,若第个图比第个图多用了个小正方形,则的值是 .
12. 如图,用大小相同的小正方形拼图,第个图是一个小正方形;第个图由个小正方形拼成;第个图由个小正方形拼成,依此规律,若第个图比第个图多用了个小正方形,则的值是 . 13. 如图,、、分别平分的外角、、内角 , 若 , 以下结论:;;;平分;其中正确的结论是填序号 .
13. 如图,、、分别平分的外角、、内角 , 若 , 以下结论:;;;平分;其中正确的结论是填序号 .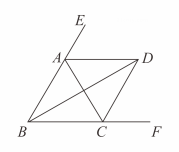
三、解答题
-
14. 【阅读理解】材料一:数形结合是解决数学问题的一种重要的思想方法,借助形的几何直观性,可以帮助理解数之间的某种关系.
 (1)、问题1:请写出图1,图2阴影部分的面积分别能解释的乘法公式.
(1)、问题1:请写出图1,图2阴影部分的面积分别能解释的乘法公式.图1: ▲ , 图2: ▲ ;
材料二:对于代数式,不同的表达形式能表现出它的不同性质.
例如代数式A=x2-4x+5,若将其写成A=(x-2)2+1的形式,因为不论x取何值,(x-2)2总是非负数,即(x-2)2≥0.
所以(x-2)2+1≥1.
所以当x=2时,A有最小值,最小值是1.
问题2:根据上述例题材料,请求代数式B=x2-2x+2的最小值.
(2)、若将代数式A写成A=(x-1)2-2(x-1)+2的形式,就能与代数式B=x2-2x+2建立联系,下面我们改变x的值,研究一下A , B两个代数式取值的规律:x
-2
-1
0
1
2
3
B=x2-2x+2
10
5
2
1
2
5
A=(x-1)2-2(x-1)+2
17
10
P
2
1
2
问题3:①上表中p的值是;
②观察表格可以发现;若x=m时,B=x2-2x+2=n , 则x=m+1时,A=x2-4x+5=n . 我们把这种现象称为代数式A参照代数式B取值延后,此时延后值为1.若代数式D参照代数式B取值延后,相应的延后值为2,则代数式D为 .
15. 【材料阅读】二元一次方程有无数组解,如: , , , , 如果我们将方程的解看成一组有序数对,那么这些有序数对可以用平面直角坐标系中的点表示,探究发现:以方程的解为坐标的点落在同一条直线上,如图1所示,同时这条直线上的点的坐标全都是该方程的解.我们把这条直线称为该方程的图象.
 (1)、【问题探究】
(1)、【问题探究】请在图2中画出二元一次方程组中的两个二元一次方程的图象,并直接写出该方程组的解为 ▲ ;
(2)、已知关于 , 的二元一次方程无解,请在图3中画出符合题意的两条直线,设方程①图象与 , 轴的交点分别是、 , 方程②图象与 , 轴的交点分别是、 , 计算的度数.(3)、【拓展应用】图4中包含关于 , 的二元一次方程组的两个二元一次方程的图象,请直接写出该方程组的解。
16. 已知:如图长方形纸片中,将长方形纸片沿直线翻折,使点落在边上,记作点 , 如图 .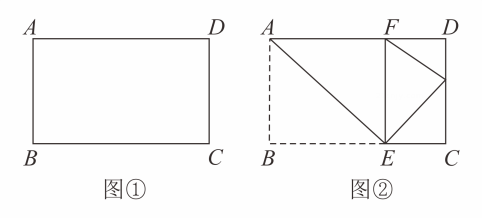 (1)、当 , 时,求线段的长度;(2)、设、 , 如果再将沿直线向右起折,使点落在射线上,记作点 , 若设线段 , 请根据题意画出图形,并求出的值;(3)、设 , , 沿直线向右翻折后交边于点 , 连接当时,求的值.17. 问题解决:
(1)、当 , 时,求线段的长度;(2)、设、 , 如果再将沿直线向右起折,使点落在射线上,记作点 , 若设线段 , 请根据题意画出图形,并求出的值;(3)、设 , , 沿直线向右翻折后交边于点 , 连接当时,求的值.17. 问题解决: (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.18.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.18. (1)、【初步感知】
(1)、【初步感知】如图1,已知△ABC为等边三角形,点D为边BC上一动点(点D不与点B , 点C重合).以AD为边向右侧作等边△ADE , 连接CE .
求证:△ABD≌△ACE;
(2)、【类比探究】如图2,若点D在边BC的延长线上,随着动点D的运动位置不同,猜想并证明:①AB与CE的位置关系为:;②线段EC、AC、CD之间的数量关系为:;
(3)、【拓展应用】如图3,在等边△ABC中,AB=3,点P是边AC上一定点且AP=1,若点D为射线BC上动点,以DP为边向右侧作等边△DPE , 连接CE、BE . 请问:PE+BE是否有最小值?若有,请直接写出其最小值;若没有,请说明理由.
19. 如图,在平面直角坐标系中,直线l与x轴相交于点P , 直线l上的两点 , 满足 , 将线段向右平移5个单位长度得到线段 .
 (1)、点C的坐标为;(2)、连接 , , , 点Q是x轴上一点(不与点P重合),连接 , 交于点E .
(1)、点C的坐标为;(2)、连接 , , , 点Q是x轴上一点(不与点P重合),连接 , 交于点E .①当恰好平分时,试判断与有什么数量关系?并说明理由;
②设点 , 记三角形的面积为S , 三角形的面积为 . 当时,求点Q的坐标.
20. (1)、如图1,若 , 求的度数;(2)、如图2,若 , 点在AB的上方,那么之间有何数量关系?并说明理由;(3)、【联想拓展】
(1)、如图1,若 , 求的度数;(2)、如图2,若 , 点在AB的上方,那么之间有何数量关系?并说明理由;(3)、【联想拓展】如图3所示,在(2)的条件下,已知的平分线和的平分线交于点 , 求的度数.
21. 如图,长方形中, , , P为长方形上的动点,动点P从A出发,沿着运动到D点停止,速度为 , 设点P运动时间为x秒,的面积为 .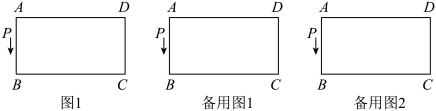 (1)、当时,对应y的值等于;时,对应y的值等于;(2)、当时,求y与x之间的关系式;(3)、当时,求对应x的值;(4)、当P在线段上运动时,是否存在点P使得的周长最小?若存在,求出此时的度数;若不存在,请说明理由.22. 如图(1), , , 垂足分别为、 , 点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束 .
(1)、当时,对应y的值等于;时,对应y的值等于;(2)、当时,求y与x之间的关系式;(3)、当时,求对应x的值;(4)、当P在线段上运动时,是否存在点P使得的周长最小?若存在,求出此时的度数;若不存在,请说明理由.22. 如图(1), , , 垂足分别为、 , 点在线段上以的速度由点向点运动,同时点在射线上运动.它们运动的时间为当点运动结束时,点运动随之结束 . (1)、AP , 用含的代数式表示;(2)、若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;(3)、如图(2),若“ , ”改为“”,点的运动速度为 , 其它条件不变,当点、运动到何处时有与全等,求出相应的的值.23. 【阅读材料】配方法是数学中重要的一种思想方法它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.
(1)、AP , 用含的代数式表示;(2)、若点的运动速度与点的运动速度相等,当时,与是否全等,并判断此时线段和线段的位置关系,请分别说明理由;(3)、如图(2),若“ , ”改为“”,点的运动速度为 , 其它条件不变,当点、运动到何处时有与全等,求出相应的的值.23. 【阅读材料】配方法是数学中重要的一种思想方法它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.我们定义:一个整数能表示成、是整数的形式,则称这个数为“完美数”例如,是“完美数”理由:因为 , 所以是“完美数”.
【解决问题】
(1)、数“完美数”填“是”或“不是”;(2)、【探究问题】已知 , 则;
(3)、已知、是整数,是常数 , 要使为“完美数”,试求出符合条件的值,并说明理由.(4)、【拓展结论】已知、满足 , 求的最小值.