2024年广东省数学八（下）期末复习：最新压轴题

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ， AB的垂直平分线交AC于点D ，交AB于点E ， $A C = 6$ ，则CD的长为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 如图，将一个邻边长分别为 $4, 8$ 的矩形纸片 $A B C D (A B = 4, B C = 8)$ 折叠，使点C与点A重合，则折痕 $E F$ 的长度为（）

A、 $2 \sqrt{5}$ B、 $\sqrt{5}$ C、 $2 \sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
3. 如图，在正方形 $A B C D$ 外取一点 $E$ ，连接 $D E$ ， $A E$ ， $C E$ ，过点 $D$ 作 $D E$ 的垂线交 $A E$ 于点 $P$ ，若 $D E = D P = 1$ ， $P C = \sqrt{6}$ ．有下列结论：① $△ A P D ≌ △ C E D$ ；② $A E ⊥ C E$ ；③点 $C$ 到直线 $D E$ 的距离为 $\sqrt{3}$ ；④ $S_{正方形 A B C D} = 5 + 2 \sqrt{2}$ ．其中正确的结论是（）

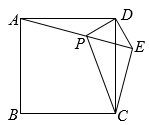A、①② B、①②③ C、①③④ D、①②④

查看试题解析
4. 如图，在赵爽弦图中，已知直角三角形的短直角边长为 $a$ ，长直角边长为 $b$ ，大正方形的面积为20，小正方形的面积为4，则 $a b$ 的值是（）

A、10 B、9 C、8 D、7

查看试题解析
5. 如图，将矩形纸片ABCD折叠，使点A与点C重合，折痕为EF，若AB=4，BC=2，那么线段EF的长为（）

A、2 $\sqrt{5}$ B、 $\sqrt{5}$ C、 $\frac{4 \sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
6. 如图，已知点 $A (0, 8)$ ， $B (0, - 2)$ ， $E (0, 5)$ ， $F (- 5, 0)$ ， $C$ 为直线 $E F$ 上一动点，则 $▱ A C B D$ 的对角线 $C D$ 的最小值是（）

A、 $2 \sqrt{2}$ B、4 C、5 D、 $2 \sqrt{3}$

查看试题解析
7. 如图， $O$ 是等边 $△ A B C$ 内一点， $O A = 6, O B = 8, O C = 10$ ，将线段 $B O$ 以点 $B$ 为旋转中心逆时针旋转 $60 °$ 得到线段 $B O^{'}$ ，下列结论：① $△ B O^{'} A$ 可以由 $△ B O C$ 绕点 $B$ 逆时针旋转 $60 °$ 得到；②点 $O$ 与 $O^{'}$ 的距离为6；③ $∠ A O B = 150 °$ ；④ $S_{四边形 A O B O^{'}} = 24 + 12 \sqrt{3}$ ；⑤ $S_{△ B O C} = 12 + 16 \sqrt{3}$ ．其中正确的结论有（）个

A、5 B、4 C、3 D、2

查看试题解析
8. 在矩形ABCD中，对角线AC、BD相交于点O ， AE平分∠BAD交BC于点E ， ∠CAE＝15°，连接OE ，则下面的结论中正确的有（　　）
①△DOC是等边三角形；②△BOE是等腰三角形；③BC＝ $\sqrt{3}$ AB；④∠AOE＝135°；⑤S_△_AOE＝S_△_BOE ．

A、2个 B、3个 C、4个 D、5个

查看试题解析
9. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+3（a＜0）交x轴于A，B两点（B在A左侧），交y轴于点C，且CO＝AO，分别以BC，AC为边向外作正方形BCDE、正方形ACGH，记它们的面积分别为S₁ ， S₂ ， △ABC面积记为S₃ ，当S₁+S₂＝6S₃时，b的值为（　　）

A、 $- \frac{1}{2}$ B、 $- \frac{2}{3}$ C、 $- \frac{3}{4}$ D、 $- \frac{4}{3}$

查看试题解析
10. 如图，将两个全等的等腰直角三角形摆成如图所示的样子，其中 $A B = A C = A G = F G$ ， $∠ B A C = ∠ A G F = 90 °$ ， $A F$ 、 $A G$ 分别与 $B C$ 交于D、E两点，将 $△ A C E$ 绕着点A顺时针旋转90°得到 $△ A B H$ ，则下列结论：① $B H ⊥ B C$ ；② $A D$ 平分 $∠ H D E$ ；③若 $B D = 3$ ，当 $D E = 2 C E$ 时，则 $A B = \frac{3}{2} \sqrt{2} + \frac{3}{2} \sqrt{3}$ ；④若 $A B$ 平分 $∠ H A D$ ，则 $S_{△ A B D} = \frac{\sqrt{2}}{2} S_{△ A D E}$ ，其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

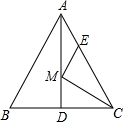
11. 如图，等边 $△ A B C$ 的周长是18，AD是BC边上的中线，M是AD上的动点，E是AC边上一点，若AE=3，EM+CM的最小值为．

查看试题解析
12. 如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则△PMN周长的最小值是．

查看试题解析
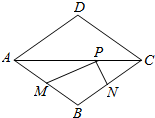13. 如图，菱形ABCD中，对角线 $A C = 6$ ， $B D = 8$ ， M，N分别是BC，CD上的动点，P是线段BD上的一个动点，则 $P M + P N$ 的最小值是．

查看试题解析
14. 已知：如图，正方形ABCD中， $A B = 2$ ， AC ， BD相交于点O ， E ， F分别为边BC ， CD上的动点（点E ， F不与线段BC ， CD的端点重合）．且 $B E = C F$ ，连接OE ， OF ， EF ．在点E ， F运动的过程中，有下列四个说法：①△OEF是等腰直角三角形；②△OEF面积的最小值是1；③至少存在一个△ECF ，使得△ECF的周长是 $2 + \sqrt{3}$ ；④四边形OECF的面积是1．其中正确的是．

查看试题解析
15. 如图，在 $△ A B C$ 中， $∠ B A C = 45 °$ ， $∠ A C B = 60 °$ ， $B C = 5$ ，将 $△ A B C$ 沿着射线 $B C$ 方向平移得到 $△ D E F$ ， A与D为对应点，连结 $C D$ ，在整个平移过程中，若 $∠ C D E = 45 °$ ，则平移的距离为.

查看试题解析
16. 如图，已知菱形 $A B C D$ 的边长为6，且 $∠ B A D = 120 °$ ，点 $E, F$ 分别在 $A B, B C$ 边上，将菱形沿 $E F$ 折叠，使点B正好落在 $A D$ 边上的点G处．若 $E G ⊥ A C$ ，则 $F G$ 的长为．

查看试题解析
17. 如图，正方形ABCD中，AD=4，点E是对角线AC上一点，连接DE，过点E作EF⊥ED，交AB于点F，连接DF，交AC于点G，将△EFG沿EF翻折，得到△EFM，连接DM，交EF于点N，若点F是AB的中点，则△EMN的周长是．

查看试题解析
18. 如图，在正方形 $A B C D$ 外取一点 $E$ ，连接 $A E$ 、 $B E$ 、 $D E$ ．过点 $A$ 作 $A E$ 的垂线交 $D E$ 于点 $P$ ．若 $A E = A P = 1$ ， $P B =$ $\sqrt{5}$ ．下列结论：① $△ A P D ≌ △ A E B$ ；②点 $B$ 到直线 $A E$ 的距离为 $\sqrt{2}$ ；③ $E B ⊥ E D$ ；④ $S_{△ A P D} + S_{△ A P B} = 1 + \sqrt{6}$ ；⑤ $S_{正方形 A B C D} = 4 + \sqrt{6}$ ．其中正确结论的序号是．

查看试题解析
19. 如图，在正方形 $A B C D$ 中， $A B = 3$ ，点 $F$ 是 $A B$ 边上一点，点 $E$ 是 $B C$ 延长线上一点， $A F = C E$ ， $B F = 2 A F$ ．连接 $D F$ 、 $D E$ 、 $E F$ ， $E F$ 与对角线 $A C$ 相交于点 $G$ ，则线段 $B G$ 的长是．

查看试题解析

三、解答题

20. 阅读材料，并解决问题：

(1)、方法指引
如图①等边 $△ A B C$ 内有一点P ，若点P到顶点A、B、C的距离分别为3，4，5，求 $∠ A P B$ 的度数．
解决本题，我们可以将 $△ A B P$ 绕顶点A旋转到 $△ A C P^{'}$ 处，此时 $△ A C P^{'} ≌ △ A B P$ ，连接 $P^{'} P$ ， $△ P A P^{'}$ 是三角形；这样利用旋转变换，我们将三条线段PA、PB、PC转化到一个三角形中，从而求出 $∠ A P B =$ °；

(2)、知识迁移
已知如图②， $△ A B C$ 中， $∠ C A B = 90 °$ ， $A B = A C$ ， E、F为BC上的点且 $∠ E A F = 45 °$ ，求证： $E F^{2} = B E^{2} + F C^{2}$ ；

(3)、能力提升
如图③，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = 1$ ， $∠ A B C = 30 °$ ，点O为 $R t △ A B C$ 内一点，连接AO ， BO ， CO ，且 $∠ A O C = ∠ C O B = ∠ B O A = 120 °$ ，求出 $O A + O B + O C$ 的值．

查看试题解析
21. 如图1，点 $P 、 Q$ 分别是边长为 $4 c m$ 的等边 $△ A B C$ 的边 $A B 、 B C$ 上的动点，点 $P$ 从顶点 $A$ ，点 $Q$ 从顶点 $B$ 同时出发，且它们的速度都为 $1 c m / s$ ．

(1)、连接 $A Q 、 C P$ 交于点 $M$ ，则在 $P 、 Q$ 运动的过程中， $∠ C M Q$ 变化吗？若变化，则说明理由；若不变，则求出它的度数；

(2)、点 $P 、 Q$ 在运动过程中，设运动时间为 $t s (0 < t < 4)$ ，当 $t$ 为何值时， $△ P B Q$ 为直角三角形？

(3)、如图2，若点 $P 、 Q$ 在运动到终点后继续在射线 $A B 、 B C$ 上运动，直线 $A Q 、 C P$ 交点为 $M$ ，在 $P 、 Q$ 运动的过程中， $∠ C M Q$ 的大小变化吗？若变化请说明理由：若不变，请求出它的度数．

查看试题解析
22. 如图1，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 60 °$ ， M为AB中点，D为射线AB上一动点．

(1)、连接CM ，求证： $△ C A M$ 是等边三角形．

(2)、当点D在线段AM上（如图1所示的位置）．
①尺规作图：连接CD ，在CD右侧作等边 $△ C D E$ ，直线DE与直线CB交于点F ．（不写作法，保留作图痕迹）
②连接BE ，在①的条件下，求证： $C E = B E$ ．

(3)、点D在射线AB运动的过程中，当 $△ B E F$ 为等腰三角形时，请求出 $∠ A B E$ 的度数．

查看试题解析
23. 如图，已知正方形ABCD ， AB＝8，点M为射线DC上的动点，射线AM交BD于E ，交射线BC于F ，过点C作CQ⊥CE ，交AF于点Q ．

(1)、当BE＝2DE时，求DM的长．

(2)、当M在线段CD上时，若CQ＝3，求MF的长．

(3)、①当DM＝2CM时，作点D关于AM的对称点N ，求tan∠NAB的值．
②若BE＝4DE ，直接写出△CQE与△CMF的面积比．

查看试题解析
24. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = 3$ ， $∠ C = 30 °$ ，点 $D$ 从点 $C$ 出发沿 $C A$ 方向以每秒2个单位长的速度向点 $A$ 匀速运动，同时点 $E$ 从点 $A$ 出发沿 $A B$ 方向以每秒1个单位长的速度向点 $B$ 匀速运动，当其中一个点到达终点，另一个点也随之停止运动．设点 $D$ 、 $E$ 运动的时间是 $t$ 秒 $(t > 0)$ ，过点 $D$ 作 $D F ⊥ B C$ 于点 $F$ ，连接 $D E$ 、 $E F$ ．

(1)、求证： $A E = D F$ ；

(2)、填空：当 $t =$ 秒时，四边形 $B E D F$ 是矩形．

(3)、四边形 $A E F D$ 能够成为菱形吗？如果能，求出相应的t值，并求出此时四边形 $A E F D$ 的面积；如果不能，说明理由．

查看试题解析
25. 如图，矩形 $O A B C$ 的顶点A、C分别在x轴、y轴的正半轴上，点B的坐标为 $(3, 4)$ ，一次函数 $y = - \frac{2}{3} x + b$ 的图象与边 $O C$ 、 $A B$ 分别交于点D、E ，且 $O D = B E$ ．点M是线段 $D E$ 上的一个动点．

(1)、求b的值；

(2)、连接 $O M$ ，若三角形 $O D M$ 的面积与四边形 $O A E M$ 的面积之比为 $1 : 3$ ，求点M的坐标；

(3)、设点N是平面内的一点，以O、D、M、N为顶点的四边形是菱形，求点N的坐标．

查看试题解析
26. 如图，在▱ABCD中，∠A＝60°，AB＝6cm ，连接BD ，恰有∠ABD＝90°，过点D作DE⊥BC于点E ．动点P从点D出发沿DA以1cm/s的速度向终点A运动，同时点Q从点B出发，以4cm/s的速度沿射线BC运动，当点P到达终点时，点Q也随之停止运动，设点P运动的时间为t s

(1)、分别求BD和BE的长度；

(2)、连接PQ ，当t= $\frac{9}{5}$ 时，判断PQ与AD是否垂直，并说明理由；

(3)、试判断是否存在t的值，使得以P ， Q ， C ， D为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由；

查看试题解析
27. 在菱形ABCD中， $∠ A = 60 °$ ，点E ， F分别是边AB ， BC上的点．

(1)、【尝试初探】如图1，若 $∠ E D F = 60 °$ ，求证： $D E = D F$ ；

(2)、【深入探究】如图2，点G ， H分别是边CD ， AD上的点，连接EG与FH相交于点O且 $∠ E O F = 60 °$ ，求证： $E G = F H$

(3)、【拓展延伸】如图3，若点E为AB的中点， $A B = 6$ ， $B F = 1$ ．
①设 $D H = x$ ， $C G = y$ ，请用关于x的代数式表示y；
②若 $C G + D H = 6$ ，求EG的长．

查看试题解析
28. 已知菱形 $A B C D$ 中， $∠ A B C = 60 °$ ，点P为菱形内部或边上一点．

(1)、如图1，若点P在对角线 $B D$ 上运动，以 $A P$ 为边向右侧作等边 $△ A P E$ ，点E在菱形 $A B C D$ 内部或边上，连接 $C E$ ，求证： $B P = C E$ ．

(2)、如图2，若点P在对角线 $B D$ 上运动，以 $A P$ 为边向右侧作等边 $△ A P E$ ，点E在菱形 $A B C D$ 的外部，若 $A B = 4$ ， $D P = 1$ ，求 $C E$ ；

(3)、如图3，若 $∠ A P B = 60 °$ ，点E，F分别在 $A P$ ， $B P$ 上，且 $A E = B F$ ，连接 $A F$ ， $E F$ ， $∠ A F E = 30 °$ ，求证： $A F^{2} + F E^{2} = A B^{2}$ ．

查看试题解析
29. 阅读与应用：
阅读1：a、b为实数，且a＞0，b＞0，因为 ${(\sqrt{a} - \sqrt{b})}^{2} \geq 0$ ，所以 $a - 2 \sqrt{a b} + b \geq 0$ 从而 $a + b \geq 2 \sqrt{a b}$ （当a=b时取等号）．
阅读2：若函数 $y = x + \frac{m}{x}$ ；（m＞0，x＞0，m为常数），由阅读1结论可知： $x + \frac{m}{x} \geq 2 \sqrt{m}$ ，所以当 $x = \frac{m}{x}$ ，即 $x = \sqrt{m}$ 时，函数 $y = x + \frac{m}{x}$ 的最小值为 $2 \sqrt{m}$ ．
阅读理解上述内容，解答下列问题：
问题1：已知一个矩形的面积为4，其中一边长为x，则另一边长为 $\frac{4}{x}$ ，周长为2（ $x + \frac{4}{x}$ ），求当x= 时，周长的最小值为；
问题2：已知函数 $y_{1} = x + 1$ （ $x > - 1$ ）与函数 $y_{2} = x^{2} + 2 x + 10$ （ $x > - 1$ ），
当x= 时， $\frac{y_{2}}{y_{1}}$ 的最小值为；
问题3：某民办学校每天的支出总费用包含以下三个部分：一是教职工工资4900元；二是学生生活费成本每人10元；三是其他费用．其中，其他费用与学生人数的平方成正比，比例系数为0.01．当学校学生人数为多少时，该校每天生均投入最低？最低费用是多少元？（生均投入=支出总费用÷学生人数）

查看试题解析
30. 如图，矩形 $A B C D$ 中，对边平行且相等，四个内角均为直角． $A B = 6$ ， $B C = 8$ ，点E是 $B C$ 边上一点，连接 $A E$ ，将 $△ A B E$ 沿 $A E$ 折叠，使点B落在点 $B^{'}$ 处，连接 $C B^{'}$ ．

(1)、当 $C B^{'} ∥ A E$ 时， $B E$ 的长为．

(2)、当点 $B^{'}$ 恰好在矩形 $A B C D$ 的对角线 $A C$ 上，求 $A E$ 的长．

(3)、当点E为 $B C$ 的中点时， $B^{'} C$ 的长为．

(4)、当 $B^{'}$ 落在矩形的对称轴上时， $B E$ 的长为．

查看试题解析
31. 如图 $△ A B C$ 与 $△ A C D$ 为正三角形，点O为射线 $C A$ 上的动点，作射线 $O M$ 与直线 $B C$ 相交于点E ，将射线 $O M$ 绕点O逆时针旋转60°，得到射线 $O N$ ，射线 $O N$ 与直线 $C D$ 相交于点F.

(1)、如图①，点O与点A重合时，点E ， F分别在线段 $B C$ ， $C D$ 上，
求证： $△ A E C ≌ △ A F D$ ；

(2)、如图②，当点O在 $C A$ 的延长线上时，E ， F分别在线段 $C B$ 的延长线和线段 $C D$ 的延长线上，请写出 $C E$ ， $C F$ ， $C O$ 三条线段之间的数量关系，并说明理由

(3)、点O在线段 $A C$ 上，若 $A B = 8$ ， $B O = 7$ ，当 $C F = 1$ 时，请直接写出 $B E$ 的长.

查看试题解析
32. 阅读下面的材料：把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例：将分式 $\frac{1 - 3 x}{x^{2} - 1}$ 表示成部分分式，解：设 $\frac{1 - 3 x}{x^{2} - 1} = \frac{M}{x + 1} + \frac{N}{x - 1}$ ，将等式右边通分，得 $\frac{M (x - 1) + N (x + 1)}{(x + 1) (x - 1)} = \frac{(M + N) x + (N - M)}{x^{2} - 1}$ ，依据题意，得 ${\begin{array}{l} M + N = 3 \\ N - M = 1 \end{array}$ ，解得 ${\begin{array}{l} M = - 2 \\ N = - 1 \end{array}$ ，所以 $\frac{1 - 3 x}{x^{2} - 1} = \frac{- 2}{x + 1} + \frac{- 1}{x - 1}$ 请你适用上面所学到的方法，解决下面的问题：

(1)、 $\frac{1}{n (n + 1)} = \frac{A}{n} + \frac{B}{n + 1}$ （A ， B为常数），则 $A =$ ， $B =$ ；

(2)、一个容器装有 $1 L$ 水，按照如下要求把水倒出：第1次倒出 $\frac{1}{2} L$ 水，第2次倒出的水量是 $\frac{1}{2} L$ 的 $\frac{1}{3}$ ，第3次倒出的水量是 $\frac{1}{3} L$ 的 $\frac{1}{4}$ ，第4次倒出的水量是 $\frac{1}{4} L$ 的 $\frac{1}{5}$ …第n次倒出的水量是 $\frac{1}{n} L$ 的 $\frac{1}{n + 1}$ …按照这种倒水的方法，这 $1 L$ 的水是否能倒完？如果能，多少次能倒完？如果不能，请说明理由；

(3)、按照（2）的条件，现在开始重新实验，按照如下要求把水倒出：第1次倒出 $\frac{1}{3} L$ 水，第2次倒出的水量是 $\frac{1}{15} L$ ，第3次倒出的水量是 $\frac{1}{35} L$ ，第4次倒出的水量是 $\frac{1}{63} L$ ，请问经过多少次操作后，杯内剩余水量能否变成原来水量的 $\frac{100}{199}$ ？试说明理由.

查看试题解析