2024年深圳市数学七(下)期末复习:精选压轴题
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 如图,在中, , 利用尺规在上分别截取 , 使 , 分别以D,E为圆心,以大于的长为半径作弧,两弧在内交于点F,作射线交于点G,若 , 过点G作交于点P,则的值为( )
 A、2 B、3 C、4 D、52. 如图,在的正方形网格中,图中的为格点三角形,在图中与成轴对称的格点三角形最多可以找出( )
A、2 B、3 C、4 D、52. 如图,在的正方形网格中,图中的为格点三角形,在图中与成轴对称的格点三角形最多可以找出( ) A、6个 B、5个 C、4个 D、3个3. 如图,已知正方形与正方形的边长分别为a,b,如果 , , 那么阴影部分的面积为( )
A、6个 B、5个 C、4个 D、3个3. 如图,已知正方形与正方形的边长分别为a,b,如果 , , 那么阴影部分的面积为( ) A、3 B、4 C、5 D、64. 如图,长方形中, , , 正方形 , 正方形和正方形都在它内部,记 , , 若 , 则长方形的面积是( )
A、3 B、4 C、5 D、64. 如图,长方形中, , , 正方形 , 正方形和正方形都在它内部,记 , , 若 , 则长方形的面积是( ) A、6 B、7 C、8 D、95. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的处接住她后用力一推,爸爸在处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和.爸爸在处接住小丽时,小丽距离地面的高度是( )
A、6 B、7 C、8 D、95. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的处接住她后用力一推,爸爸在处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和.爸爸在处接住小丽时,小丽距离地面的高度是( )
 A、1m B、1.6m C、 D、6. 【观察】①;
A、1m B、1.6m C、 D、6. 【观察】①;②;
③;
……
【归纳】由此可得:;
【应用】请运用上面的结论,计算:( )
A、 B、 C、 D、7. 如图,中, , , 是斜边的中点,是直角边上一动点,连接交于 , 过作交的延长线于点 , 交于点 , 则下列结论:
;
;
;
, 其中正确的是( )
A、 B、 C、 D、8. 如图,已知正方形与正方形的边长分别为、 , 如果 , , 则阴影部分的面积为( ) A、38 B、39 C、40 D、419. 如图,长方形中,点为上一点,连接 , 将长方形沿着直线折叠,点恰好落在的中点上,点为的中点,点为线段上的动点,连接、 , 若、、 , 则的最小值是( )
A、38 B、39 C、40 D、419. 如图,长方形中,点为上一点,连接 , 将长方形沿着直线折叠,点恰好落在的中点上,点为的中点,点为线段上的动点,连接、 , 若、、 , 则的最小值是( ) A、 B、 C、 D、10. 如图①所示(图中各角均为直角),动点从点出发,沿路线匀速运动,的面积随点运动的时间之间的函数关系图象如图②所示,已知 , 下列说法错误的是( )
A、 B、 C、 D、10. 如图①所示(图中各角均为直角),动点从点出发,沿路线匀速运动,的面积随点运动的时间之间的函数关系图象如图②所示,已知 , 下列说法错误的是( ) A、动点P的速度为 B、的值为30 C、EF的长度为 D、当时,的值为811. 如图, , , 是中点.连接 , 连接交于点 , 连接交于点 , 作射线交于点 . 给出结论:①是中点;②;③;④ , 其中正确的有( )
A、动点P的速度为 B、的值为30 C、EF的长度为 D、当时,的值为811. 如图, , , 是中点.连接 , 连接交于点 , 连接交于点 , 作射线交于点 . 给出结论:①是中点;②;③;④ , 其中正确的有( ) A、1个 B、2个 C、3个 D、4个12. 如图,在正方形中,点E,F,G,H分别是正方形各边的中点,则下列结论不正确的是( )
A、1个 B、2个 C、3个 D、4个12. 如图,在正方形中,点E,F,G,H分别是正方形各边的中点,则下列结论不正确的是( ) A、 B、 C、 D、阴影部分面积为正方形面积的
A、 B、 C、 D、阴影部分面积为正方形面积的二、填空题
-
13. 如图,中,点是的垂直平分线与的交点,交延长于点 , 若 , , , 则的面积为 .
 14. 任意选取四个连续的自然数,将它们的积再加上1,所得的结果可以用一个自然数的平方表示.如:.设这四个连续的自然数分别为 , 则 , 其中“"用含的式子表示为.15. 如图,中, , 点为延长线上一点,于点 , 点为延长线上一点,连接交的延长线于点 , 点是的中点,若 , , 则.
14. 任意选取四个连续的自然数,将它们的积再加上1,所得的结果可以用一个自然数的平方表示.如:.设这四个连续的自然数分别为 , 则 , 其中“"用含的式子表示为.15. 如图,中, , 点为延长线上一点,于点 , 点为延长线上一点,连接交的延长线于点 , 点是的中点,若 , , 则. 16. 如图,点 , 分别是角两边、上的定点, , . 点 , 分别是边 , 上的动点,则的最小值是 .
16. 如图,点 , 分别是角两边、上的定点, , . 点 , 分别是边 , 上的动点,则的最小值是 . 17. 如图,在中,将对折,使和在同一直线上,折痕为 , 延长至点D,使得 , 连接 , 若 , 则 .
17. 如图,在中,将对折,使和在同一直线上,折痕为 , 延长至点D,使得 , 连接 , 若 , 则 . 18. 如图,点在线段上, , , , 若 , , 则的度数为 .
18. 如图,点在线段上, , , , 若 , , 则的度数为 . 19. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则.
19. 如图,在四边形ABCD中,是边BC的中点,AE平分且 , 若 , , 则. 20. .如图,在等腰中,AB=AC=11,BC=8,∠A=40°,等腰中,DE=DF=5,∠EDF=70°,则周长为 .
20. .如图,在等腰中,AB=AC=11,BC=8,∠A=40°,等腰中,DE=DF=5,∠EDF=70°,则周长为 . 21. 如图,直线l为线段 的垂直平分线,垂足为C , 直线l上的两点E , F位于 异侧(E , F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是 .
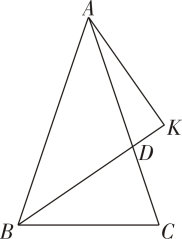
21. 如图,直线l为线段 的垂直平分线,垂足为C , 直线l上的两点E , F位于 异侧(E , F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是 .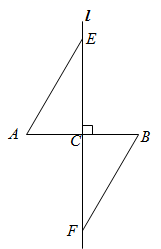 22. 如图,在等腰中, , , 为的角平分线,过点作交的延长线与点 , 若 , 则的长为 .
22. 如图,在等腰中, , , 为的角平分线,过点作交的延长线与点 , 若 , 则的长为 . 23. 如图,在中,点是上一点,连接 , , 过点作于点 , 交于点 , 且:: , 若 , , 则的长为 .
23. 如图,在中,点是上一点,连接 , , 过点作于点 , 交于点 , 且:: , 若 , , 则的长为 .
三、解答题
-
24. 在小学,我们知道正方形具有性质“四条边都相等,四个内角都是直角”,请适当利用上述知识,解答下列问题:
已知:如图,在正方形中, , 点G是射线上的一个动点,以为边向右作正方形 , 作于点H.
 (1)、填空:°;(2)、若点G在点B的右边.
(1)、填空:°;(2)、若点G在点B的右边.①求证:;
②试探索:的值是否为定值,若是,请求出定值;若不是,请说明理由.
(3)、连接 , 在G点的整个运动(点G与点A重合除外)过程中 , 求的度数;25. 如图,已知是等腰直角三角形,点P以的速度从点B出发沿着射线运动,连接 . 以为直角边向右作等腰直角 , 其中 , 连接 , 设运动时间为t秒. (1)、当时,则cm,°;(2)、在点P的运动过程中,能否使为等腰三角形?若能,求出此时t的值;若不能,请说明理由;(3)、请用含t的代数式直接写出的面积.26. 【材料阅读】小明在学习完全等三角形后,为了进一步探究,他尝试用三种不同方式摆放一副三角板(在中, , ;中, , ),并提出了相应的问题.
(1)、当时,则cm,°;(2)、在点P的运动过程中,能否使为等腰三角形?若能,求出此时t的值;若不能,请说明理由;(3)、请用含t的代数式直接写出的面积.26. 【材料阅读】小明在学习完全等三角形后,为了进一步探究,他尝试用三种不同方式摆放一副三角板(在中, , ;中, , ),并提出了相应的问题. (1)、【发现】
(1)、【发现】如图1,将两个三角板互不重叠地摆放在一起,当顶点摆放在线段上时,过点作 , 垂足为点 , 过点作 , 垂足为点 ,
①请在图10-1找出一对全等三角形,在横线上填出推理所得结论;
,
,
, ,
, ,
,
,
,
;
② , , 则;
(2)、【类比】如图2,将两个三角板叠放在一起,当顶点在线段上且顶点在线段上时,过点作 , 垂足为点 , 猜想 , , 的数量关系,并说明理由;
(3)、【拓展】如图3,将两个三角板叠放在一起,当顶点在线段上且顶点在线段上时,若 , , 连接 , 则的面积为 .
27.(1)、如图1,在中,是BC边上一点,且 , 若 , 则. (2)、如图2,在中,是BC边上一点, , 点在线段AD上且 , 求证:.
(2)、如图2,在中,是BC边上一点, , 点在线段AD上且 , 求证:. (3)、如图3,在中,是CB延长线上一点, , 点在射线DA上且 , 请画出点的位置,此时AB和CE满足怎样的数量关系,请说明理由.
(3)、如图3,在中,是CB延长线上一点, , 点在射线DA上且 , 请画出点的位置,此时AB和CE满足怎样的数量关系,请说明理由. 28.(1)、【初步感知】
28.(1)、【初步感知】如图1,已知△ABC为等边三角形,点D为边BC上一动点(点D不与点B,点C重合).以AD为边向右侧作等边△ADE,连接CE.

求证:
(2)、【类比探究】如图2,若点D在边BC的延长线上,随着动点D的运动位置不同,猜想并证明:①AB与CE的位置关系为: ▲ ;②线段EC、AC、CD之间的数量关系为: ▲ .
 (3)、【拓展应用】
(3)、【拓展应用】如图3,在等边△ABC中,AB=3,点P是边AC上一定点且AP=1,若点D为射线BC上动点,以DP为边向右侧作等边DPE,连接CE、BE.
请问:PE+BE是否有最小值?若有,请直接写出其最小值:若没有,请说明理由.
 29. “等面积法”是解决三角形内部线段长度的常用方法.如图1,在中, , 作 , 若 , , , 可列式: , 解得.
29. “等面积法”是解决三角形内部线段长度的常用方法.如图1,在中, , 作 , 若 , , , 可列式: , 解得. (1)、在题干的基础上,
(1)、在题干的基础上,①如图2,点为上一点,作 , , 设 , , 求证:;
②如图3,当点在延长线上时,猜想、之间又有什么样的数量关系,请证明你的猜想;
(2)、如图4,在中, , , .若点是延长线上一点,且 , 过点作 , 点是直线上一动点,点是直线上一动点,连接、 , 求的最小值.30. 在中, . (1)、【特例感知】
(1)、【特例感知】如图1,如果平分交于点D, , 垂足E在的延长线上,则线段和有怎样的数量关系?请说明理由;
(2)、【问题探究】如图2,点D是边上一点,连接 , 过点A作于点E,过点C作 , 交的延长线于点F,则线段和有怎样的数量关系?请说明理由;
(3)、【拓展应用】如图3,点D是边上一点,连接 , 过点C作 , 交的延长线于点E,连接 , 若 , 则 .
31. 定理:三角形任意两边之和大于第三边. (1)、如图1,线段 , 交于点 , 连接 , , 判断与的大小关系,并说明理由;(2)、如图2,平分 , 为上任意一点,在 , 上截取 , 连接 , . 求证:;(3)、如图3,在中, , 为角平分线上异于端点的一动点,求证: .32. 【问题背景】中, , , 点D为直线上一点.(1)、【初步探究】
(1)、如图1,线段 , 交于点 , 连接 , , 判断与的大小关系,并说明理由;(2)、如图2,平分 , 为上任意一点,在 , 上截取 , 连接 , . 求证:;(3)、如图3,在中, , 为角平分线上异于端点的一动点,求证: .32. 【问题背景】中, , , 点D为直线上一点.(1)、【初步探究】如图,当点D在线段上时,连接 , 过点A作于点A,且 , 过点E作于H点,交于F点.
求证: .
请将证明过程补充完整:

证明: , , 即 .
, ,
( ),
▲ ( ).
为等腰直角三角形, , ,
在中,
,
.
在与中,
,
( ).(2)、【推广探究】如图,若点D为边BC延长线上一点,其他条件不变,则(1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
 (3)、【拓展应用】
(3)、【拓展应用】若 , , 其它条件不变时, .
33. (1)、【问题发现】
(1)、【问题发现】如图 , 与中, , , 、、三点在同一直线上, , , 则 .
(2)、【问题提出】如图 , 在中, , , 过点作 , 且 , 求的面积.
(3)、【问题解决】如图 , 四边形中, , 面积为且的长为 , 求的面积.
34. 在等腰中, , 点是射线上的动点,垂直于直线于点 , 交直线于点 . (1)、【探索发现】如图①,若点在的延长线上,点在线段上时,请猜想 , , 之间的数量关系为;(2)、【拓展提升】如图②,若点在线段上(不与点 , 重合),试猜想 , , 之间的数量关系,并说明理由:(3)、【灵活应用】当 , 时,直接写出线段的长为
(1)、【探索发现】如图①,若点在的延长线上,点在线段上时,请猜想 , , 之间的数量关系为;(2)、【拓展提升】如图②,若点在线段上(不与点 , 重合),试猜想 , , 之间的数量关系,并说明理由:(3)、【灵活应用】当 , 时,直接写出线段的长为