2024年深圳市数学七(下)期末复习:最新压轴题
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 如图,已知 , 点C在EF上, , BC平分∠DCF , 且AC⊥BC . 则下列结论:①;②;③ . 其中正确的个数有( )
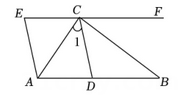 A、①② B、①③ C、②③ D、①②③2. 如图,在长方形中, , , 对角线 , 动点从点出发,沿运动.设点的运动路程为 , 的面积为 . 若与的对应关系如图所示.则图中( )
A、①② B、①③ C、②③ D、①②③2. 如图,在长方形中, , , 对角线 , 动点从点出发,沿运动.设点的运动路程为 , 的面积为 . 若与的对应关系如图所示.则图中( ) A、 B、1 C、3 D、43. 某种细菌每分钟可由1个分裂成2个,将1个细菌放在培养瓶中经过64分钟就能分裂满一瓶.若将4个这种细菌放入同一个培养瓶中,分裂满一瓶的时间是( )A、16分钟 B、32分钟 C、52分钟 D、62分钟4. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 , , 若CD∥BE , , 则的度数是( )
A、 B、1 C、3 D、43. 某种细菌每分钟可由1个分裂成2个,将1个细菌放在培养瓶中经过64分钟就能分裂满一瓶.若将4个这种细菌放入同一个培养瓶中,分裂满一瓶的时间是( )A、16分钟 B、32分钟 C、52分钟 D、62分钟4. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 , , 若CD∥BE , , 则的度数是( ) A、 B、 C、 D、5. 合并同类项m﹣3m+5m﹣7m+…+2013m的结果为( )
A、 B、 C、 D、5. 合并同类项m﹣3m+5m﹣7m+…+2013m的结果为( )
A、0 B、1007m C、m D、以上答案都不对6. 甲从深圳匀速骑电动车到广州,乙从广州匀速骑摩托车到深圳,两人同时出发,到达目的地后,立即停止运动,甲、乙两人离深圳的距离与他们骑车的时间之间的函数关系如图所示,则下列说法错误的是( ) A、深广两地的距离为 B、甲的速度为 C、乙的速度为 D、乙运动到达深圳7. 如图,一副三角板中两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°,保持三角板ABC不动,三角板DCE可绕点C旋转,则下列结论:①∠ACE=∠BCD;②∠BCE+∠ACD随着∠ACD的交化而变化;③当AB∥CE时,则∠ACD=60°或150°;④当∠BCE=3∠ACD时,DE一定垂直于AC.其中正确的个数是( )
A、深广两地的距离为 B、甲的速度为 C、乙的速度为 D、乙运动到达深圳7. 如图,一副三角板中两个直角顶点C叠放在一起,其中∠A=30°,∠B=60°,∠D=∠E=45°,保持三角板ABC不动,三角板DCE可绕点C旋转,则下列结论:①∠ACE=∠BCD;②∠BCE+∠ACD随着∠ACD的交化而变化;③当AB∥CE时,则∠ACD=60°或150°;④当∠BCE=3∠ACD时,DE一定垂直于AC.其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
8. 如图(一)所示的这种拼图(宽度设为acm)我们小时候可能都玩过,已知有若干片相同的拼图,且拼图依相同方向排列时可紧密拼成一行,如图(二)所示,当4片拼图紧密拼成一行时长度为19cm;如图(三)所示,当10片拼图紧密拼成一行时长度为46cm,则这样一片拼图的宽度a为cm.
 9. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板.小深先用一副七巧板拼成了图1,图1的轮廓是一个边长为的正方形,其中 , 小等腰直角三角板的面积为 , 小深拿掉七巧板中的一块,又将剩下的六块拼成一个新的图形,其轮廓和板的位置如图2所示,则图2的面积为 .
9. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,经过历代演变而成七巧板.小深先用一副七巧板拼成了图1,图1的轮廓是一个边长为的正方形,其中 , 小等腰直角三角板的面积为 , 小深拿掉七巧板中的一块,又将剩下的六块拼成一个新的图形,其轮廓和板的位置如图2所示,则图2的面积为 . 10. 如图,在长方形中 , , 点E , F是边 , 上的点, , 且 , 分别以 , 为边在长方形外侧作正方形和 , 若长方形的面积为20,则图中阴影部分的面积和为
10. 如图,在长方形中 , , 点E , F是边 , 上的点, , 且 , 分别以 , 为边在长方形外侧作正方形和 , 若长方形的面积为20,则图中阴影部分的面积和为 11. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .
11. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .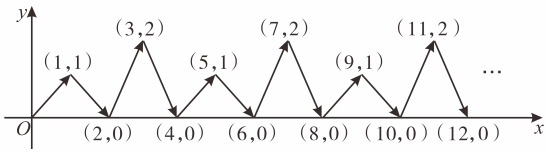 12. 电影《哈利•波特》中,小哈利波特穿越墙进入“ 站台”的镜头(如示意图的Q站台),构思奇妙,能给观众留下深刻的印象.若A、B站台分别位于﹣ , 处,AP=2PB,则P站台用类似电影的方法可称为“站台”.
12. 电影《哈利•波特》中,小哈利波特穿越墙进入“ 站台”的镜头(如示意图的Q站台),构思奇妙,能给观众留下深刻的印象.若A、B站台分别位于﹣ , 处,AP=2PB,则P站台用类似电影的方法可称为“站台”.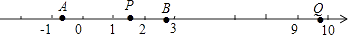 13. 如图,长方形在平面直角坐标系中,其中 , , 点是的中点,动点从点出发,以每秒的速度沿 运动,最终到达点 . 若点运动的时间为秒,那么当的面积等于时,点坐标为.
13. 如图,长方形在平面直角坐标系中,其中 , , 点是的中点,动点从点出发,以每秒的速度沿 运动,最终到达点 . 若点运动的时间为秒,那么当的面积等于时,点坐标为. 14. 如图,△ABC中,D是AB的中点,且 , , 则.
14. 如图,△ABC中,D是AB的中点,且 , , 则.
三、解答题
-
15. 多项式乘法的学习中,等式可以用平面图形(图)的面积来说明.
 (1)、【初步探究】
(1)、【初步探究】请使用(图)的种规格的正方形,设计一个平面图形方案说明等式是正确的;
(2)、【知识拓展】
为进一步探索部分平面图形的面积与等式的关系,在某次数学活动中,准备(图)所示的三种规格的正方形、长方形卡片若干张.小明从中选取张,拼成一个边长为的正方形,请你写出与其面积相应的等式;(3)、【延伸应用】
请利用()中得到的等式解答以下问题:若实数 , 满足 , , 求的值.16. 【阅读材料】我们知道,图形也是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,而运用代数思想也能巧妙地解决些图形问题.在一次数学活动课上,张老师准备了若干张如图1所示的甲、乙、丙三种纸片,其中甲种纸片是边长为x的正方形,乙种纸片是边长为y的正方形,丙种纸片是长为y , 宽为x的长方形.并用甲种纸片一张,乙种纸片一张,丙种纸片两张拼成了如图2所示的一个大正方形.
 (1)、【理解应用】
(1)、【理解应用】观察图2,用两种不同方式表示阴影部分的面积可得到一个等式,请你直接写出这个等式.
(2)、【拓展升华】利用(1)中的等式解决下列问题.
①已知 , , 求的值;
②已知 , 求的值.
17. 任意一个无理数介于两个整数之间,我们定义,若无理数T: , (其中m为满足不等式的最大整数,n为满足不等式的最小整数),则称无理数T的“麓外区间”为(m , n),如 , 所以的麓外区间为(1,2).
(1)、无理数的“麓外区间”是;(2)、实数x , y , m满足关系式:求m的算术平方根的“麓外区间”.
(3)、若某一个无理数T的“麓外区间”为(m , n),其中是关于x , y的二元一次方程的一组正整数解,请求出m、n的值,并写出一个符合题意的无理数T .18. 【问题背景】光线照射到镜面会产生反射现象,小圳在做镜面反射实验时发现:当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.例如:在图1中,有 .
 (1)、【初步探究】如图2,设镜子AB与BC的夹角 , 当时,小圳发现入射光线EF与反射光线GH恰好平行.(2)、【深入探究】如图3,小圳渐渐改变两镜面之间夹角,使得是一个锐角,从F点发出一条光线EF经过2次反射又回到了点F , 入射光线EF与第2次反射光线GF的夹角为 . 用含的式子表示 .(3)、【拓展应用】如图4,小圳继续改变两镜面之间夹角,使得 , 若也是一个钝角,入射光线EF与镜面AB的夹角 . 已知入射光线EF从镜面AB开始反射,经过3次反射,当第3次反射光线与入射光线EF平行时,求出的度数.19. 综合与实践:综合与实践活动课上,孙老师让同学们以“奇妙的平行线”为主题开展数学活动.如图1, , 点、分别在射线和上, .
(1)、【初步探究】如图2,设镜子AB与BC的夹角 , 当时,小圳发现入射光线EF与反射光线GH恰好平行.(2)、【深入探究】如图3,小圳渐渐改变两镜面之间夹角,使得是一个锐角,从F点发出一条光线EF经过2次反射又回到了点F , 入射光线EF与第2次反射光线GF的夹角为 . 用含的式子表示 .(3)、【拓展应用】如图4,小圳继续改变两镜面之间夹角,使得 , 若也是一个钝角,入射光线EF与镜面AB的夹角 . 已知入射光线EF从镜面AB开始反射,经过3次反射,当第3次反射光线与入射光线EF平行时,求出的度数.19. 综合与实践:综合与实践活动课上,孙老师让同学们以“奇妙的平行线”为主题开展数学活动.如图1, , 点、分别在射线和上, . (1)、若 , 则=度;探究中小聪同学发现,过点作即可得到的度数,请直接写出的度数;(2)、小明同学发现:无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图2,过点作 , 交于 , 请你根据小明同学提供的辅助线,先确定该定值,并说明理由;(3)、如图3,把“”改为“” (),其它条件保持不变,猜想与的数量关系,并说明理由.20. 如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a-30|+(b+6)2=0.点O是数轴原点。
(1)、若 , 则=度;探究中小聪同学发现,过点作即可得到的度数,请直接写出的度数;(2)、小明同学发现:无论如何变化,的值始终为定值,并给出了一种证明该发现的辅助线作法:如图2,过点作 , 交于 , 请你根据小明同学提供的辅助线,先确定该定值,并说明理由;(3)、如图3,把“”改为“” (),其它条件保持不变,猜想与的数量关系,并说明理由.20. 如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a-30|+(b+6)2=0.点O是数轴原点。 (1)、点A表示的数为 , 点B表示的数为 , 线段AB的长为。(2)、若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为。(3)、现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?21. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)、点A表示的数为 , 点B表示的数为 , 线段AB的长为。(2)、若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为。(3)、现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?21. 如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补. (1)、求证:AB∥CD;(2)、如图2,∠AEF与∠EFC的角平分线相交于点P,直线EP与直线CD交于点G,过点G做EG的垂线,交直线MN于点H.求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点,且∠PHK=∠HPK,作∠EPK的平分线交直线MN于点Q.问∠HPQ的大小是否发生变化?若不变,请求出∠HPQ的度数;若变化,请说明理由.22. 【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,中, , , 求边上的中线的取值范围.
(1)、求证:AB∥CD;(2)、如图2,∠AEF与∠EFC的角平分线相交于点P,直线EP与直线CD交于点G,过点G做EG的垂线,交直线MN于点H.求证:PF∥GH;(3)、如图3,在(2)的条件下,连接PH,K是GH上一点,且∠PHK=∠HPK,作∠EPK的平分线交直线MN于点Q.问∠HPQ的大小是否发生变化?若不变,请求出∠HPQ的度数;若变化,请说明理由.22. 【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,中, , , 求边上的中线的取值范围.经过组内合作交流,小明得到了如下的解决方法:延长到点E , 使.请根据小明的方法思考:
 (1)、请证明(2)、请直接写出的取值范围;(3)、【问题解决】请利用上述方法(倍长中线)解决问题.
(1)、请证明(2)、请直接写出的取值范围;(3)、【问题解决】请利用上述方法(倍长中线)解决问题.如图2,已知 , , , P为的中点.若A , C , D共线,求证:平分;