2024年浙教版数学八(下)期末复习:精选压轴题(4)
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 已知实数满足 , 设 , 则的最大值为( )A、3 B、4 C、5 D、62. 如图,在矩形中, , 对角线的垂直平分线与边 , 分别交于点 , , 则的长为( )
 A、 B、 C、 D、53. 如图,在第一象限内,点A是一次函数图象上一动点,点B,C的坐标分别是 , , 若反比例函数和的图象分别经过点A,D,则下列代数式的值为定值的是( )
A、 B、 C、 D、53. 如图,在第一象限内,点A是一次函数图象上一动点,点B,C的坐标分别是 , , 若反比例函数和的图象分别经过点A,D,则下列代数式的值为定值的是( ) A、 B、 C、 D、4. 如图,在中, , 分别以AB、AC为边向外作正方形ABDE和AFGC.若想要求出的面积,则只需知道以下哪个图形的面积( )
A、 B、 C、 D、4. 如图,在中, , 分别以AB、AC为边向外作正方形ABDE和AFGC.若想要求出的面积,则只需知道以下哪个图形的面积( )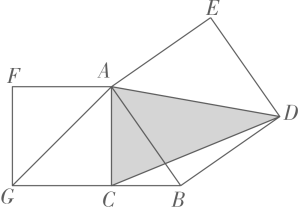 A、 B、 C、正方形ABDE D、四边形AFGB5. 如图,在正方形ABCD中,点F在边CD上(不与点C,点D重合),点E是CB延长线上的一点,且满足BE=DF,连接EF,过点A作 AH⊥EF,垂足是点H,连接BH.设AB=a,BE=b,BH=c,则( )
A、 B、 C、正方形ABDE D、四边形AFGB5. 如图,在正方形ABCD中,点F在边CD上(不与点C,点D重合),点E是CB延长线上的一点,且满足BE=DF,连接EF,过点A作 AH⊥EF,垂足是点H,连接BH.设AB=a,BE=b,BH=c,则( ) A、2c=a+b B、 C、 D、2c2=a2+b6. 如图,在中,以BC和AD为斜边分别向内作等腰和等腰 , 延长BE和DG分别交AG和CE于点H和F,直线FH分别交AD和BC于点I和J.若四边形EFGH是正方形,的面积为S,下列哪条线段的长度不能用S来表示( )
A、2c=a+b B、 C、 D、2c2=a2+b6. 如图,在中,以BC和AD为斜边分别向内作等腰和等腰 , 延长BE和DG分别交AG和CE于点H和F,直线FH分别交AD和BC于点I和J.若四边形EFGH是正方形,的面积为S,下列哪条线段的长度不能用S来表示( ) A、AB B、BC C、CE D、IJ7. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形与正方形 , 点O为对角线的中点,过点O,分别交 , 于点M,N,若 , , 连 . 则的值为( )
A、AB B、BC C、CE D、IJ7. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形与正方形 , 点O为对角线的中点,过点O,分别交 , 于点M,N,若 , , 连 . 则的值为( ) A、 B、 C、 D、8. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
A、 B、 C、 D、8. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、49. 如图,在中,以和为斜边分别向内作等腰和等腰 , 延长和分别交和于点H和F,直线分别交和于点和 . 若四边形是正方形,的面积为 , 下列哪条线段的长度不能用来表示( )
A、1 B、 C、2 D、49. 如图,在中,以和为斜边分别向内作等腰和等腰 , 延长和分别交和于点H和F,直线分别交和于点和 . 若四边形是正方形,的面积为 , 下列哪条线段的长度不能用来表示( ) A、 B、 C、 D、10. 如图,在矩形中,对角线 , 交于点 , 点为边上一点,过分别作 , , 垂足为点 , , 过作 , 垂足为 . 若知道与的周长和,则一定能求出( )
A、 B、 C、 D、10. 如图,在矩形中,对角线 , 交于点 , 点为边上一点,过分别作 , , 垂足为点 , , 过作 , 垂足为 . 若知道与的周长和,则一定能求出( ) A、的周长 B、的周长 C、的周长 D、四边形的周长11. 如图,是锐角三角形,是的中点,分别以 , 为边向外侧作等腰三角形和等腰三角形 . 点 , 分别是底边 , 的中点,连接 , , 若(是锐角),则的度数是( )
A、的周长 B、的周长 C、的周长 D、四边形的周长11. 如图,是锐角三角形,是的中点,分别以 , 为边向外侧作等腰三角形和等腰三角形 . 点 , 分别是底边 , 的中点,连接 , , 若(是锐角),则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 如图,矩形纸片ABCD中,是AD上一点,将沿CE对折得到 , 延长CF交AB于点 , 恰有 , 则AE的长为.
 13. 如图,在平面直角坐标系中,平行四边形的边与反比例函数的图象交于两点,且与轴正半轴交于点 , 点在反比例函数的图象上.若点是的中点,则平行四边形的面积为 , .
13. 如图,在平面直角坐标系中,平行四边形的边与反比例函数的图象交于两点,且与轴正半轴交于点 , 点在反比例函数的图象上.若点是的中点,则平行四边形的面积为 , . 14. 在一张边长为的正方形纸片上剪下一个一边长为的等腰三角形,要求:等腰三角形的三个顶点都落在正方形的边上,且其中一个顶点与正方形的顶点重合,则所的等腰三角形的面积可能是(写出至少三个)
14. 在一张边长为的正方形纸片上剪下一个一边长为的等腰三角形,要求:等腰三角形的三个顶点都落在正方形的边上,且其中一个顶点与正方形的顶点重合,则所的等腰三角形的面积可能是(写出至少三个) 15. 如图是一张矩形纸片ABCD,点E在边BC上,且满足 AB=2BE,把△ABE沿直线AE折叠,使点B落在点F处,EF的延长线与边CD交于点G.若CG=DG,则= .
15. 如图是一张矩形纸片ABCD,点E在边BC上,且满足 AB=2BE,把△ABE沿直线AE折叠,使点B落在点F处,EF的延长线与边CD交于点G.若CG=DG,则= . 16. 如图,在平面直角坐标系xOy中,正方形ABCD的顶点A、C恰好落在双曲线上,且点O在AC上,AD交x轴于点E.①当A点坐标为时,D点的坐标为;②当CE平分时,正方形ABCD的面积为.
16. 如图,在平面直角坐标系xOy中,正方形ABCD的顶点A、C恰好落在双曲线上,且点O在AC上,AD交x轴于点E.①当A点坐标为时,D点的坐标为;②当CE平分时,正方形ABCD的面积为. 17. 如图,正方形的边长为2,点M是边上的一动点,连接交对角线于点G,作的中垂线交于点F,当时, .
17. 如图,正方形的边长为2,点M是边上的一动点,连接交对角线于点G,作的中垂线交于点F,当时, . 18. 如图,在平面直角坐标系中,正方形的两邻边分别在坐标轴的正半轴上,E为x轴正半轴上一动点,连 , 过点B作交y轴于点F,连 , 以 , 为邻边构造平行四边形 , 已知 .
18. 如图,在平面直角坐标系中,正方形的两邻边分别在坐标轴的正半轴上,E为x轴正半轴上一动点,连 , 过点B作交y轴于点F,连 , 以 , 为邻边构造平行四边形 , 已知 . (1)、当E为的中点时,点F坐标为 .(2)、在点E运动过程中,最小值为 .19. 如图,在中, , 点D为边的中点,点E在边上, , 将沿BE折叠至 , 当时,则 .
(1)、当E为的中点时,点F坐标为 .(2)、在点E运动过程中,最小值为 .19. 如图,在中, , 点D为边的中点,点E在边上, , 将沿BE折叠至 , 当时,则 . 20. 如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为;②当平分时,正方形的面积为 .
20. 如图,在平面直角坐标系中,正方形的顶点A、C恰好落在双曲线上,且点O在上,交x轴于点E.①当A点坐标为时,D点的坐标为;②当平分时,正方形的面积为 .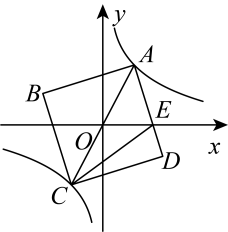 21. 如图,点 , 在反比例函数( , )的图象上,点 , 在反比例函数( , )的图象上,且轴,过 , 分别作轴的垂线,垂足为 , , 交于点 , 连结交于点 . 若 , 则 .
21. 如图,点 , 在反比例函数( , )的图象上,点 , 在反比例函数( , )的图象上,且轴,过 , 分别作轴的垂线,垂足为 , , 交于点 , 连结交于点 . 若 , 则 .
三、解答题
-
22. 根据以下素材,完成探索任务.
探索果园土地规划和销售利润问题
素材1
某农户承包了一块长方形果园ABCD,图1是果园的平面图,其中AB=200米,BC=300米.准备在它的四周铺设道路,上下两条横向道路的宽度都为2x米,左右两条纵向道路的宽度都为x米,中间部分种植水果.已知道路的路面造价是50元/m²;出于货车通行等因素的考虑,道路宽度不超过12米,且不小于5米.

素材2
该农户发现某一种草莓销售前景比较不错,经市场调查,草莓培育一年可产果,已知每平方米的草莓销售平均利润为100元;果园每年的承包费为25万元,期间需一次性投入33万元购进新苗,每年还需25万元的养护、施肥、运输等其余费用.

问题解决
任务1
解决果园中路面宽度的设计对种植面积的影响.
⑴请直接写出纵向道路宽度x的取值范围.
⑵若中间种植的面积是44800m2 , 则路面设置的宽度是否符合要求.
任务2
解决果园种植的预期利润问题.(净利润=草莓销售的总利润一路面造价费用一果园承包费用一新苗购置费用一其余费用,
⑶经过l年后,农户是否可以达到预期净利润400万元?请说明理由.
23. 如图,过原点的直线交双曲线于点和点 , 点的坐标为 , 点是双曲线上异于点的动点,且点在第一象限,作直线交双曲线于点 . 连结 , , , . (1)、以下是小明同学探究四边形是平行四边形的过程,请你补充完整:
(1)、以下是小明同学探究四边形是平行四边形的过程,请你补充完整:∵双曲线关于原点成中心对称,且过原点的直线与双曲线交于点和点 ,
∴ .
同理 .
∴四边形是平行四边形.
(2)、问题探究:①是否可能为矩形?请说明理由.
②是否可能为菱形?请说明理由.
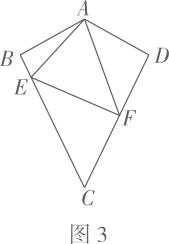
(3)、当的面积为18时,求点的坐标.24. 定义:一组邻边相等,另一组邻边也相等的凸四边形叫做“筝形”.如在凸四边形ABCD中,若 , 则四边形ABCD是“筝形”.(1)、【新知学习】如图1,在边长为1的正方形网格中,画出“筝形”ABCD,要求点D是格点;
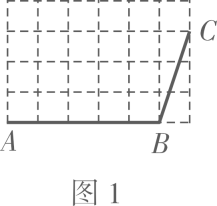 (2)、【问题探究】
(2)、【问题探究】如图2,在矩形ABCD中, , “筝形”EFGH的顶点是AB的中点,点F,G,H分别在BC,CD,AD上,且 , 求对角线EG的长;
 (3)、【拓展思考】
(3)、【拓展思考】如图3,在“筝形”ABCD中,分别是BC、CD上的点,AE平分 , 求“筝形”ABCD的面积.
 25. 定义:把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形.
25. 定义:把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形. (1)、矩形勾股四边形(填“是”或“不是”).(2)、如图在直角坐标系xOy中,直线与双曲线相交于A,B两点,点在x轴负半轴上,Q为直角坐标平面上一点.
(1)、矩形勾股四边形(填“是”或“不是”).(2)、如图在直角坐标系xOy中,直线与双曲线相交于A,B两点,点在x轴负半轴上,Q为直角坐标平面上一点.①分别求出A、B两点的坐标.
②当四边形APQB是平行四边形时,如图(1),请证明是勾股四边形.
(3)、在(2)的条件下,当以A、B、P、Q为顶点的四边形是勾股四边形时,请直接写出Q点的坐标.26. 如图1,在菱形中, . 等腰的两个顶点分别在上,且 , 点在的异侧.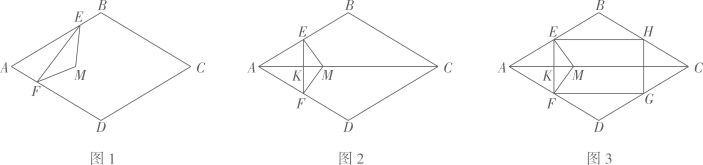 (1)、如图2,当于点时,
(1)、如图2,当于点时,①求证: , 且点在菱形的对角线上.
②如图3,若交于点交于点 , 连结 . 当 时,四边形为正方形.
(2)、如图1,①判断:点 ▲ 菱形的对角线上.(填“在”或“不在”)
②若 , 请求出的取值范围.
27. 如图,是的中位线,点M为射线上的一个动点(不与点E重合),作交边于点F,连接 .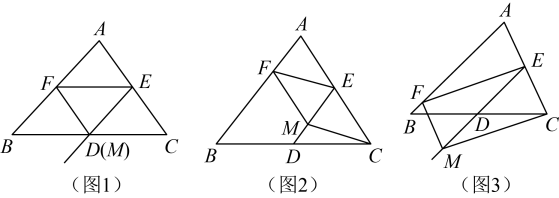 (1)、如图1,当点M与点D重合时,求证:四边形是平行四边形;(2)、如图2, , , 点M在线段上运动,当四边形是菱形时, , 求菱形的面积;(3)、如图3, , 在延长线上(可以与点D重合)存在一点M,使得四边形为矩形,求的度数范围.28. 在正方形中.
(1)、如图1,当点M与点D重合时,求证:四边形是平行四边形;(2)、如图2, , , 点M在线段上运动,当四边形是菱形时, , 求菱形的面积;(3)、如图3, , 在延长线上(可以与点D重合)存在一点M,使得四边形为矩形,求的度数范围.28. 在正方形中.
 (1)、【发现】
(1)、【发现】如图1,为对角线上一点,连接 , . 则与相等吗?说明理由.
(2)、【应用】如图2,点在上,连接 , , 延长交于点 , 交的延长线于点 , 若 , 且 , 求正方形的边长.
(3)、【迁移】若正方形的边长为 , 点在射线上,连接 , , 射线交直线于点 , 请问:是否存在点 , 使得为等腰三角形?若存在,求出该三角形的腰长;若不存在,试说明理由.
29. 如图,已知正方形的边长为2,点是边上的一动点,平分交边于点 . (1)、①当点恰好是边的中点时,求线段长;②当点恰好是边CD的中点时,求线段长.(2)、猜想线段 , , 之间的数量关系,并说明理由.(3)、直接写与面积和的最大值.30. 定义:把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形.(1)、矩形勾股四边形(填“是”或“不是”).(2)、如图在直角坐标系中,直线y=-x+1与双曲线相交于A,B两点,点在x轴负半轴上,Q为直角坐标平面上一点.
(1)、①当点恰好是边的中点时,求线段长;②当点恰好是边CD的中点时,求线段长.(2)、猜想线段 , , 之间的数量关系,并说明理由.(3)、直接写与面积和的最大值.30. 定义:把能被一条对角线分成两个全等直角三角形的四边形叫做勾股四边形.(1)、矩形勾股四边形(填“是”或“不是”).(2)、如图在直角坐标系中,直线y=-x+1与双曲线相交于A,B两点,点在x轴负半轴上,Q为直角坐标平面上一点.
①分别求出A、B两点的坐标.
②当四边形是平行四边形时,如图,请证明是勾股四边形.
(3)、在(2)的条件下,当以A、B、P、Q为顶点的四边形是勾股四边形时,请直接写出Q点的坐标.