2024年浙教版数学八(下)期末复习:精选压轴题(2)
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 在平面直角坐标系中,有 , , 三点,另有一点D与点A,B,C构成平行四边形,则点D的坐标不可能是( )A、 B、 C、 D、2. 已知关于x的一元二次方程 , 及函数 , (a,b,c为常数,且),则( )A、若方程有解,则函数的图象一定有交点 B、若方程有解,则函数的图象一定没有交点 C、若方程无解,则函数的图象一定有交点 D、若方程无解,则函数的图象一定没有交点3. 如图所示,在一张长为 , 宽为的矩形纸片上,现要剪下一个腰长为的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积不可能是( )
 A、 B、 C、 D、4. 将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形和正方形 . 现将四个直角三角形的较长直角边分别向外延长,且 , , , , 得到图2所示的“新型数学风车”的四个叶片,即 , , , . 若平分 , 正方形和正方形的边长比为 , 若“新型数学风车”的四个叶片面积和是 , 则正方形EFGH的面积是( )
A、 B、 C、 D、4. 将四个全等的直角三角形作为叶片按图1摆放成一个风车形状,形成正方形和正方形 . 现将四个直角三角形的较长直角边分别向外延长,且 , , , , 得到图2所示的“新型数学风车”的四个叶片,即 , , , . 若平分 , 正方形和正方形的边长比为 , 若“新型数学风车”的四个叶片面积和是 , 则正方形EFGH的面积是( ) A、 B、 C、 D、5. 四边形ABCD和CEFG都是正方形,在CD上,连结AF交对角线BD于点 , 交DE于点.若要求两正方形的面积之和,则只需知道( )
A、 B、 C、 D、5. 四边形ABCD和CEFG都是正方形,在CD上,连结AF交对角线BD于点 , 交DE于点.若要求两正方形的面积之和,则只需知道( ) A、IF的长 B、BH的长 C、AH的长 D、CI的长6. 如图,是锐角三角形,是的中点,分别以 , 为边向外侧作等腰三角形和等腰三角形 . 点 , 分别是底边 , 的中点,连接 , , 若(是锐角),则的度数是( )
A、IF的长 B、BH的长 C、AH的长 D、CI的长6. 如图,是锐角三角形,是的中点,分别以 , 为边向外侧作等腰三角形和等腰三角形 . 点 , 分别是底边 , 的中点,连接 , , 若(是锐角),则的度数是( ) A、 B、 C、 D、7. 如图,在矩形中, , 连接 , , 与对角线交于点 , 且 , , 有下列三个结论:①;②;③ . 其中,正确的是( )
A、 B、 C、 D、7. 如图,在矩形中, , 连接 , , 与对角线交于点 , 且 , , 有下列三个结论:①;②;③ . 其中,正确的是( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
8. 如图,在正方形中, , 点是的中点,连结 , 则;点F在边AB上,将△BCF沿CF折叠,点B恰好落在CE上的点G处,连结EF,则 .
 9. 如图,已知在平面直角坐标系中,点P在反比例函数图象上,点B为y轴负半轴上一点,连结交x轴于点A,点C为x轴负半轴上一点,连结和 . 若 , , 且的面积为3,则k的值是 .
9. 如图,已知在平面直角坐标系中,点P在反比例函数图象上,点B为y轴负半轴上一点,连结交x轴于点A,点C为x轴负半轴上一点,连结和 . 若 , , 且的面积为3,则k的值是 . 10. 如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点 , 交轴于点 , 连结BO并延长交该反比例函数图象的另一支于点 , 连结AE交轴于点 , 连结BF,OA,且.
10. 如图,直线AB交反比例函数的图象于A,B两点,(点A,B在第一象限,且点在点的左侧),交轴于点 , 交轴于点 , 连结BO并延长交该反比例函数图象的另一支于点 , 连结AE交轴于点 , 连结BF,OA,且.
①若 , 则.
②若 , 则的值为.
11. 如图,在菱形ABCD中, , , 将菱形ABCD沿菱形ABCD某一边平移a长度,得菱形;将菱形沿菱形某一边平移a长度,得菱形;将菱形沿菱形某一边平移a长度,得菱形;若四个菱形构成的整个图形为中心对称图形,且四个菱形重叠部分面积为 , 则 . 12. 如图,菱形中, , M为边上的一点,将菱形沿折叠后,点A恰好落在的中点E处,则 .
12. 如图,菱形中, , M为边上的一点,将菱形沿折叠后,点A恰好落在的中点E处,则 . 13. 如图,在矩形中, , 点P在上,不与点C,点D重合,连接 , , 为直角三角形,当满足条件的P点有且只有一个时, .
13. 如图,在矩形中, , 点P在上,不与点C,点D重合,连接 , , 为直角三角形,当满足条件的P点有且只有一个时, . 14. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .
14. 如图,在平行四边形中, , , 是边延长线上一点,连接 , 以为边作等边三角形 , 连接 , 则的最小值是 .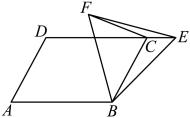
三、解答题
-
15. 根据以下素材,探索完成任务
如何设计拱桥上救生圈的悬挂方案?
素材1
图1是一座抛物线形拱桥,以抛物线两个水平最低点连线为x轴,抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系,如图2所示.
某时测得水面宽 , 拱顶离水面最大距离为10m,抛物线拱形最高点与x轴的距离为5m.据调查,该河段水位在此基础上再涨1m达到最高.

素材2
为方便救助溺水者,拟在图1的桥拱上方栏杆处悬挂救生圈,如图3,救生圈悬挂点为了方便悬挂,救生圈悬挂点距离抛物线拱面上方1m,且相邻两救生圈悬挂点的水平间距为4m.为美观,放置后救生圈关于y轴成轴对称分布.(悬挂救生圈的柱子大小忽略不计)

问题解决
任务1
确定桥拱形状
根据图2,求抛物线的函数表达式.
任务2
拟定设计方案
求符合悬挂条件的救生圈个数,并求出最右侧一个救生圈悬挂点的坐标.
任务3
探究救生绳长度
当水位达到最高时,上游个落水者顺流而下到达抛物线拱形桥面的瞬间,若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边,求救生绳至少需要多长.(救生圈大小忽略不计,结果保留整数)
16. 在矩形中,是边上一动点,将矩形沿着对折,点的对应点为 .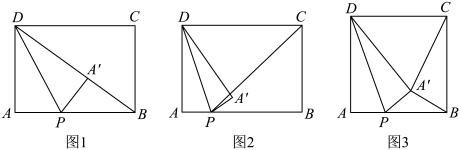 (1)、若 , .
(1)、若 , .①如图1,当点恰好落在对角线上时,求的长.
②如图2,是射线上一动点,当 , , 三点在同一直线上时,求的长.
(2)、如图3,若 , 连结 , , 当是直角时,求的长.17. 根据以下素材,完成探索任务:如何故剪出符合要求的矩形纸片?
素材1
如图1,是腰长为的等腰直角三角形卡纸,甲,乙、丙三名同学分别用这样的卡纸试图裁剪出不一样的矩形纸片,并使长方形的四个顶点都在的边上.

素材2
甲同学按图2的方式裁剪,想裁出面积为的矩形纸片,乙同学按图3的方式裁剪,想裁出两边长之比为的矩形纸片,丙同学想裁出面积最大的矩形纸片.
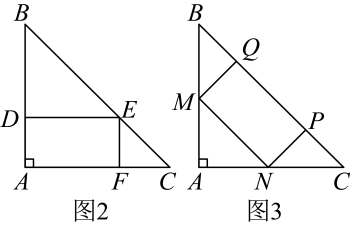
任务1
计算矩形纸片的边长
请帮甲同学计算此矩形纸片的两边长
任务2
计算矩形纸片的面积
请求出符合乙同学裁剪方案的矩形纸片的面积
任务3
计算矩形纸片的最大面积
请帮丙同学计算出面积最大的矩形纸片的面积
18. 如图,已知在菱形中, , , 对角线与交于点O,点E是射线上的一个动点,将线段绕点D顺时针旋转得到线段 , 连结 , , . (1)、如图1,当点E在线段上运动时,
(1)、如图1,当点E在线段上运动时,①求证:;
②当时,判断四边形的形状,并说明理由.
(2)、在点E的整个运动过程中,将沿着DE翻折得到四边形 , 当四边形为菱形时,求出此时的面积.19. 已知 , 分别以为边,在的上侧作正方形和正方形 . (1)、如图1,若点E在边上,判断的形状,并说明理由.(2)、如图2,当点F在边上时,设 .
(1)、如图1,若点E在边上,判断的形状,并说明理由.(2)、如图2,当点F在边上时,设 .①求证: .
②如图3,再以为边,也在的上侧作正方形 , 且M在边上,当点F,M,N三点共线时,求a,b所满足的数量关系式.
20. 如图,在正方形中,点G在对角线上,不与点B,D重合,连接并延长交于点E,连接并延长交于点M,过点D作交于点P,交于N,垂足为F.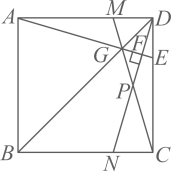 (1)、求证:;(2)、求证:;(3)、若 , , 求的长.(用含a的式子表示)21. 在中, , , 将绕点C顺时针旋转到 , 其中点A,点B的对应点分别为点E,点D,连结 .
(1)、求证:;(2)、求证:;(3)、若 , , 求的长.(用含a的式子表示)21. 在中, , , 将绕点C顺时针旋转到 , 其中点A,点B的对应点分别为点E,点D,连结 .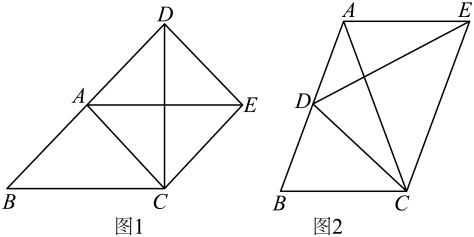 (1)、如图1,当点D在线段的延长线上时,
(1)、如图1,当点D在线段的延长线上时,①证明:四边形是平行四边形.
②若点A为的中点,求四边形的面积.
(2)、如图2,当点D在线段上时,若点D为的中点,求的长.22. 如图,直线分别与反比例函数和的图象交于A,B两点,点B横坐标为2. (1)、求n的值.(2)、若点C为图像上一点,过点C作直线轴,交反比例函数于点D,当时,求C点横坐标.(3)、若点E在直线AB上,请在坐标平面内找一点F,使得以C,D,E,F四点为顶点的四边形是正方形,并求出点F的坐标.23. 如图,已知,正方形ABCD的边长为4,点是CD边上一点,点P,Q分别在边AD和BC上,且.
(1)、求n的值.(2)、若点C为图像上一点,过点C作直线轴,交反比例函数于点D,当时,求C点横坐标.(3)、若点E在直线AB上,请在坐标平面内找一点F,使得以C,D,E,F四点为顶点的四边形是正方形,并求出点F的坐标.23. 如图,已知,正方形ABCD的边长为4,点是CD边上一点,点P,Q分别在边AD和BC上,且. (1)、如图1,若点是CD中点.
(1)、如图1,若点是CD中点.①当点P和点重合时,画出图形,求BQ的长,并说明理由.
②AP=m,BQ=n.请探究m,n之间的关系.
(2)、如图2, , 连接BP,PE,若 , 求BQ的长. (3)、如图3,若点E是CD中点,连结BP,QE.请直接写出所有情形下的最小值.
(3)、如图3,若点E是CD中点,连结BP,QE.请直接写出所有情形下的最小值.