2024年浙教版数学八(下)期末复习:精选压轴题(1)
试卷更新日期:2024-06-02 类型:复习试卷
一、单选题
-
1. 七巧板是我们祖先的一项卓越创造,被西方人誉为“东方魔板”.已知如图所示是一副正方形七巧板(相同的板规定序号相同).现从七巧板中取出四块(序号可以相同)拼成一个小正方形(无空隙不重叠),则可以拼成的序号是( )
 A、②③③④ B、①①②③ C、①①②④ D、①①②⑤2. 如图,将菱形沿折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设 , , , 则关系正确的是( )
A、②③③④ B、①①②③ C、①①②④ D、①①②⑤2. 如图,将菱形沿折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设 , , , 则关系正确的是( )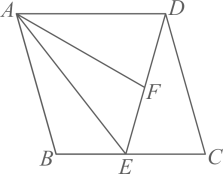 A、 B、 C、 D、3. 如图,在菱形中, , , 点E是点A关于直线的对称点,连结交于点F,连结 , , 则的长是( )
A、 B、 C、 D、3. 如图,在菱形中, , , 点E是点A关于直线的对称点,连结交于点F,连结 , , 则的长是( ) A、16.8 B、19.2 C、19.6 D、204. 已知一次函数的图象与的图象交于点 . 则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,5. 延时课上,王林用四根长度都为4cm的木条制作了图1所示正方形,而后将正方形的BC边固定,平推成图2的图形,并测得∠B=60°,则在此变化过程中结论错误的是( )
A、16.8 B、19.2 C、19.6 D、204. 已知一次函数的图象与的图象交于点 . 则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,5. 延时课上,王林用四根长度都为4cm的木条制作了图1所示正方形,而后将正方形的BC边固定,平推成图2的图形,并测得∠B=60°,则在此变化过程中结论错误的是( ) A、AB长度不变,为4cm B、AC长度变小,减少4 C、BD长度变大,增大4 D、ABCD面积变小,减少6. 将一张矩形纸片(不是正方形),先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形,剩下的是如图所示的四边形纸片 , 其中 , , , , 则这张矩形纸片的较长边不可能是( )
A、AB长度不变,为4cm B、AC长度变小,减少4 C、BD长度变大,增大4 D、ABCD面积变小,减少6. 将一张矩形纸片(不是正方形),先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形,剩下的是如图所示的四边形纸片 , 其中 , , , , 则这张矩形纸片的较长边不可能是( ) A、6 B、 C、 D、87. 如图,在中(), , 对角线交于点 , 动点从点出发,沿着→→运动.设点E运动的路程为 , 的面积为 , 关于的函数图象如图所示.则长为( )
A、6 B、 C、 D、87. 如图,在中(), , 对角线交于点 , 动点从点出发,沿着→→运动.设点E运动的路程为 , 的面积为 , 关于的函数图象如图所示.则长为( )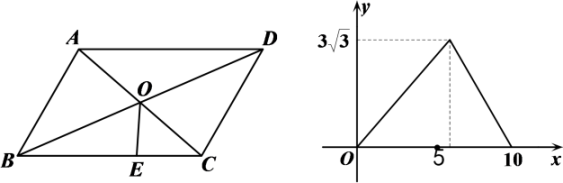 A、5 B、6 C、 D、8. 已知一次函数的图象与的图象交于点.则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,9. 如图,在正方形中,已知点是线段上的一个动点(点与点不重合),作交于点 . 现以 , 为邻边构造平行四边形 , 连接 , 则的最小值为( )
A、5 B、6 C、 D、8. 已知一次函数的图象与的图象交于点.则对于不等式 , 下列说法正确的是( )A、当时, B、当时, C、当且时, D、当且时,9. 如图,在正方形中,已知点是线段上的一个动点(点与点不重合),作交于点 . 现以 , 为邻边构造平行四边形 , 连接 , 则的最小值为( ) A、 B、 C、 D、10. 如图,将两个等腰直角三角形和拼接在正方形ABCD内部,其中 , 下列结论:①四边形AECF是平行四边形:②△ABF是直角三角形:③若 , 则其中正确结论的编号是( )
A、 B、 C、 D、10. 如图,将两个等腰直角三角形和拼接在正方形ABCD内部,其中 , 下列结论:①四边形AECF是平行四边形:②△ABF是直角三角形:③若 , 则其中正确结论的编号是( ) A、①② B、①③ C、②③ D、①②③
A、①② B、①③ C、②③ D、①②③二、填空题
-
11. 已知是完全平方式,则常数的值是 .12. 有学者认为,阿拉伯数学家花拉子米的《代数学》关于一元二次方程的几何求解法与中国古代数学的“出入相补原理”相近,可能受到中国传统数学思想的影响,花拉子米关于的几何求解方法如图1,在边长为x的正方形的四个边上向外做边长为x和的矩形,再把它补充成一个边长为的大正方形,我们得到大正方形的面积为(因为).所以大正方形边长为 , 得到 . 思考:当我们用这种方法寻找的解时,如图2中间小正方形的边长x为;阴影部分每个正方形的边长为 .
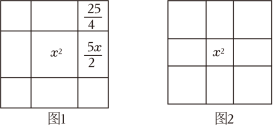 13. 如图,在中, , 在内取一点G,使点G到三角形三边距离 , , 都相等,连结 , , 已知 , .
13. 如图,在中, , 在内取一点G,使点G到三角形三边距离 , , 都相等,连结 , , 已知 , . (1)、若 , 则的长是(用含m的代数式表示);(2)、当 , 时,的值为 .14. 如图,正方形的边长为 , 点分别在上,且 , 与交于点 , 若四边形的面积为 , 则 .
(1)、若 , 则的长是(用含m的代数式表示);(2)、当 , 时,的值为 .14. 如图,正方形的边长为 , 点分别在上,且 , 与交于点 , 若四边形的面积为 , 则 . 15. 如图,正方形ABCD的对角线AC,BD相交于点O,AE平分∠BAC分别交BC,BD于点E,点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F,则OM与OG存在数量关系;当OM=1时,则BM= .
15. 如图,正方形ABCD的对角线AC,BD相交于点O,AE平分∠BAC分别交BC,BD于点E,点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F,则OM与OG存在数量关系;当OM=1时,则BM= . 16. 如图,已知在平面直角坐标系中,点P是对角线的中点,反比例函数的图象经过点A,点P.若的面积为30,且y轴将的面积分为 , 则k的值为 .
16. 如图,已知在平面直角坐标系中,点P是对角线的中点,反比例函数的图象经过点A,点P.若的面积为30,且y轴将的面积分为 , 则k的值为 . 17. 如图,在平面直角坐标系中,反比例函数是常数)在第一象限部分的图象与矩形OABC的两边AB和BC分别交于D,F两点,将沿OD翻折得到的延长线恰好经过点.若 , 则的值是.
17. 如图,在平面直角坐标系中,反比例函数是常数)在第一象限部分的图象与矩形OABC的两边AB和BC分别交于D,F两点,将沿OD翻折得到的延长线恰好经过点.若 , 则的值是. 18. 如图,在菱形中, , , 将向右平移得到(点在线段上),连接 . 在平移过程中,
18. 如图,在菱形中, , , 将向右平移得到(点在线段上),连接 . 在平移过程中,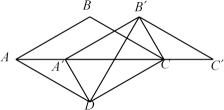 (1)、若四边形是矩形,则;(2)、的最小值为 .19. 如图,正方形ABCD的边长为4,点E,F分别在BC,CD上,且与BF交于点 , 若四边形OFCE的面积为3,则.
(1)、若四边形是矩形,则;(2)、的最小值为 .19. 如图,正方形ABCD的边长为4,点E,F分别在BC,CD上,且与BF交于点 , 若四边形OFCE的面积为3,则. 20. 如图,在菱形中,已知 , , 点是对角线上的一个动点,连结 , 将沿边翻折得到 , 连结 .
20. 如图,在菱形中,已知 , , 点是对角线上的一个动点,连结 , 将沿边翻折得到 , 连结 . (1)、度.(2)、若是以为腰的等腰三角形,则的值为 .
(1)、度.(2)、若是以为腰的等腰三角形,则的值为 .三、解答题
-
21. 如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=2OB,反比例函数 在第一象限的图象经过正方形的顶点C.
 (1)、求点C的坐标;(2)、如图2,将正方形ABCD沿x轴向右平移得到正方形 A'B'CD',点 A'恰好落在反比例函数的图象上,求此时点 D'的坐标;(3)、在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.22. 综合实践:
(1)、求点C的坐标;(2)、如图2,将正方形ABCD沿x轴向右平移得到正方形 A'B'CD',点 A'恰好落在反比例函数的图象上,求此时点 D'的坐标;(3)、在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.22. 综合实践:项目主题
“亚运主题”草坪设计
项目情境
为了迎亚会,同学们参与一块长为40米,宽为30米的矩形“亚运主题”草
坪方案设计的项目学习.以下为项目学习小组对草坪设计的研究过程.
活动任务一
请设计两条相同宽度的小路连接矩形草坪两组对边.小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案

驱动问题一
(1)项目小组设计出来的四种方案小路面积的大小关糸?
①直观猜想:我认为 ▲ ;(请用简洁的语言或代数式表达你的猜想)
②具体验证:选择最简单的甲、乙方案,假设小路宽为1米,则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ;
③一般验证:若小路宽为x米,则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ .
活动任务二
为施工方便,学校选择甲种方案设计,并要求除小路后草坪面积约为1064平方米.
驱动问题二
(2)请计算两条小路的宽度是多少?
活动任务三
为了布置五环标志等亚运元素,将在草坪上的亚运宣传主题墙前,用篱笆围(三边)成面积为100平方米的矩形 , 如图.
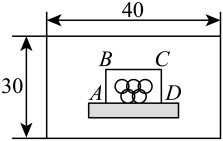
驱动问题三
(3)为了使篱笆恰好用完同时围住三面,项目小组的同学对下列问题展开探究,其中矩形宽 , 长 .
①若30米长的篱笆,请用两种不同的函数表示y关于x的函数关系.
②数学之星小明提出一个问题:若a米长的篱笆恰好用完,且有两种不同方案可以选择,使得两种方案的宽之和小于15米,甲同学说“篱笆的长可以是28米”,乙同学说“篱笆的长可以是32米”,你认为他们俩的说法对吗?请说明理由.
23. 在某探究课《矩形的折叠》中,每个小组分到了相同大小的矩形纸张 , , , 各小组通过对该纸张的折叠探究了各种不同的折叠问题.小组
探究内容
图形
第一小组
把沿折叠,与重叠部分记为 .

第二小组
步骤:1:把矩形沿折叠,使得与重合,点E,F分别为上的点.
步骤2:P为边上动点(与点B,C不重合),沿折叠得到 .

第三小组
步骤1:把矩形沿折叠,使得与重合,点G,H分别为上的点.
步骤2:P为边上动点(与点B,C不重合),
沿过点P的一条折痕折叠得到 .

根据以上各小组探究内容,求解下列问题.
(1)、根据第一小组探究内容,求证:是等腰三角形.(2)、根据第二小组探究内容,当P, , E三点在同一直线上时,求的长度.(3)、根据第三小组探究内容,过点P的折痕使落在线段上,请直接写出折痕条数与长度取值范围的关系.24. 如图,平面直角坐标系中,正方形的边在x轴上,点B在第一象限.点D是对角线上的动点,作交x轴于点E,作的平分线交y轴于点F.点A坐标为 . (1)、若点D的横坐标为3,求点F的纵坐标.(2)、若点D的横坐标为4,求点E的坐标.(3)、连接 , 当是含的直角三角形,直接写出点D的坐标.25. 已知菱形ABCD和等边△CEF,∠ABC=60°,
(1)、若点D的横坐标为3,求点F的纵坐标.(2)、若点D的横坐标为4,求点E的坐标.(3)、连接 , 当是含的直角三角形,直接写出点D的坐标.25. 已知菱形ABCD和等边△CEF,∠ABC=60°, (1)、当E,F分别在CA,CB的延长线上时(如图1),连结AF,DE.
(1)、当E,F分别在CA,CB的延长线上时(如图1),连结AF,DE.①求证:AF=DE:
②连结DF,交AB于点N(如图2),取AE的中点M,连结MN.若AE=AC=3,求MN的长:
(2)、当点F在DA的延长线上时(如图3),连结AE,DE,分别取AE,DF的中点M,N,连结MN.若AC=2,CE= , 求MN的长,26. 如图1,为矩形的对角线,的平分线交于点 , 交的延长线于点 . 点是线段上的动点,以为对角线作正方形(点 , , , 按顺时针方向排列). (1)、求证: .(2)、已知 , .
(1)、求证: .(2)、已知 , .①如图2,若点落在边上,求的值;
②在点的运动过程中,是否存在某一位置,使得正方形的某边落在的一边上?若存在,求的长;若不存在,请说明理由.
27. 如图,在中,过点A作交直线于点F,且 , 平分交于点E,交于点G,过点A作交直线于点H. (1)、求证:;(2)、若 , , 求线段的长;(3)、下列三个问题,依次为易、中、难,对应的满分值为1分、2分、3分,根据你的认知水平,选择其中一个问题求解.
(1)、求证:;(2)、若 , , 求线段的长;(3)、下列三个问题,依次为易、中、难,对应的满分值为1分、2分、3分,根据你的认知水平,选择其中一个问题求解.①当点F与点C重合时,求证:;
②当点F在延长线上,且时,求证:;
③当点F在线段上时,求证:.
28. 如图1,在矩形ABCD中, , 点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,使点落在CD边上的处,点落在处,连接.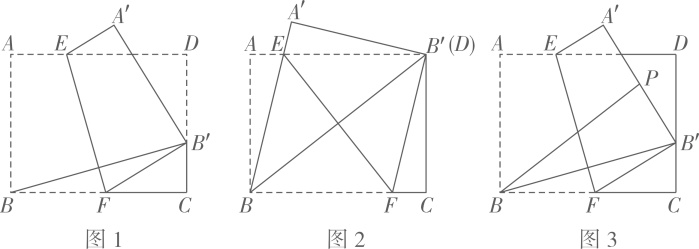 (1)、如图2,若点与点重合,连接EB
(1)、如图2,若点与点重合,连接EB①请你判断四边形的形状,并证明;
②求的长;
(2)、如图3,P为中点,连接BP.①当=2时,求BP的长;
②直接写出BP的取值范围.
29. 如图1,在矩形中, , , 点E,F分别在 , 上,将矩形沿直线折叠,使点B落在边上的处,点A落在处,连接 . (1)、如图2,若点与点D重合,连接 .
(1)、如图2,若点与点D重合,连接 .
①请你判断四边形的形状,并证明;
②求的长;
(2)、如图3,P为中点,连接 .
①当时,求的长;
②直接写出的取值范围.
30. 如图1,在平面直角坐标系中,矩形的顶点 , 分别在轴,轴的正半轴上,且点的坐标为 , 点为线段上的一个动点,点为线段上一点(不与点重合),连结 . (1)、求对角线所在直线的函数表达式.(2)、如图2,将沿着翻折,使点落在平面内的点处.若点为对角线的中点,当点恰好落在矩形的顶点上时,求的长.(3)、如图3,连结 , 延长交边于点 . 当时,坐标平面内是否存在点 , 使得以 , , , 为顶点的四边形是菱形?若存在,请求出点P的坐标,若不存在,请说明理由.
(1)、求对角线所在直线的函数表达式.(2)、如图2,将沿着翻折,使点落在平面内的点处.若点为对角线的中点,当点恰好落在矩形的顶点上时,求的长.(3)、如图3,连结 , 延长交边于点 . 当时,坐标平面内是否存在点 , 使得以 , , , 为顶点的四边形是菱形?若存在,请求出点P的坐标,若不存在,请说明理由.