2024年浙教版数学七（下）期末复习：解答题压轴题

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、解答题

1. 定义：若分式 $M$ 与分式 $N$ 的差等于它们的积，即 $M - N = M N$ ，则称分式N是分式 $M$ 的“互联分式”．如 $\frac{1}{x + 1}$ 与 $\frac{1}{x + 2}$ ，因为 $\frac{1}{x + 1} - \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ， $\frac{1}{x + 1} \times \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ，所以 $\frac{1}{x + 2}$ 是 $\frac{1}{x + 1}$ 的“互联分式”．

(1)、判断分式 $\frac{3}{x + 2}$ 与分式 $\frac{3}{x + 5}$ 是否是“互联分式”，请说明理由；

(2)、小红在求分式 $\frac{1}{x^{2} + y^{2}}$ 的“互联分式”时，用了以下方法：
设 $\frac{1}{x^{2} + y^{2}}$ 的“互联分式”为 $N$ ，则 $\frac{1}{x^{2} + y^{2}} - N = \frac{1}{x^{2} + y^{2}} \times N$ ，
$∴ (\frac{1}{x^{2} + y^{2}} + 1) N = \frac{1}{x^{2} + y^{2}}$ ， $∴ N = \frac{1}{x^{2} + y^{2} + 1}$ ．
请你仿照小红的方法求分式 $\frac{x + 2}{x + 5}$ 的“互联分式”．

(3)、解决问题：
仔细观察第（1）（2）小题的规律，请直接写出实数 $a$ ， $b$ 的值，使 $\frac{4 a - 2}{b x + b}$ 是 $\frac{4 b + 2}{b x + a}$ 的“互联分式”．

查看试题解析
2. 阅读材料：我们把多项式 $a^{2} + 2 a b + b^{2}$ 及 $a^{2} - 2 a b + b^{2}$ 叫做完全平方式．如果一个多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式的最大值，最小值等．
例如：分解因式： $x^{2} + 2 x - 3 = (x^{2} + 2 x + 1) - 4 = {(x + 1)}^{2} - 4 = (x + 1 + 2) (x + 1 - 2) = (x + 3) (x - 1)$ ；

又例如：求代数式 $2 x^{2} + 4 x - 6$ 的最小值：∵ $2 x^{2} + 4 x - 6 = 2 (x^{2} + 2 x - 3) = 2 {(x + 1)}^{2} - 8$ ，

又∵ ${(x + 1)}^{2} \geq 0$ ；

∴当 $x = - 1$ 时， $2 x^{2} + 4 x - 6$ 有最小值，最小值是 $- 8$ ．

根据阅读材料，利用“配方法”，解决下列问题：

(1)、分解因式： $a^{2} + 6 a + 8 =$ ．

(2)、已知实数 $a$ ， $b$ 满足 $a^{2} - 8 b = 12 a - b^{2} - 52$ ，求 $2 a + b$ 的值；

(3)、当 $x =$ 、 $y =$ 时，多项式 $- 2 x^{2} - 2 x y - y^{2} + 8 x - 7$ 的最大值．

查看试题解析
3. 将一副直角三角板 $A B C$ 和 $D E F$ 如图（1）放置，此时 $F ， B ， E ， C$ 四点在同一条直线上，点A在边 $D F$ 上，其中 $∠ A B C = ∠ D E F = 90 °$ ， $∠ E D F = 30 °$ ， $∠ B A C = 45 °$ ．

(1)、求 $∠ C A D$ 的度数；

(2)、将图（1）中的三角板 $D E F$ 绕点A以每秒 $10 °$ 的速度，按顺时针方向旋转一定的角度 $a ° (0 ° < a ° < 360 °)$ 后，记为三角板 $D^{'} E^{'} F^{'}$ ，设旋转的时间为t秒．
①当旋转至图（2）时，此时 $D^{'} E^{'} ⊥ A C$ ，求a的值；
②若在旋转过程中，三角板 $D^{'} E^{'} F^{'}$ 的某一边恰好与 $B C$ 所在的直线平行，直接写出t的值．

查看试题解析
4. 如图，已知数轴上点 $A$ 表示的数为12， $B$ 是数轴上位于点 $A$ 左侧一点，且 $A B = 32$ ，动点 $P$ 从点 $A$ 出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为 $t$ 秒．

(1)、数轴上点 $B$ 表示的数是，点 $P$ 表示的数是（用含 $t$ 的代数式表示）；

(2)、若 $M$ 为线段 $A P$ 的中点， $N$ 为线段 $B P$ 的中点，在点 $P$ 运动的过程中，线段 $M N$ 的长度会发生变化吗？如果不变，请求出这个长度；如果会变化，请用含 $t$ 的代数式表示这个长度；

(3)、动点 $Q$ 从点 $B$ 处出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点 $P$ 、 $Q$ 同时出发，问点 $P$ 运动多少秒时与点 $Q$ 相距4个单位长度？

查看试题解析

5. 某工厂需制作如图所示的竖式与横式两种无盖纸盒(单位cm).

情境	内容	图形
情境1	工厂仓库内现存有35cm×35cm的正方形纸板200张，35cm×50cm的长方形纸板400张，用库存纸板制作两种无盖纸盒.
情境2	库存纸板已用完，采购部重新采购了如图规格的纸板，甲纸板尺寸为50cm×70cm，乙纸板尺寸为35cm×85cm，丙纸板尺寸为35cm×70cm.采购甲纸板有800张，乙纸板有400张，丙纸板有300张．纸板裁剪后可制作两种无盖纸盒.
情境3	某次采购订单中，甲种纸板的采购数量为500张，乙种300张，因采购单被墨水污染，导致丙种纸板的具体数字已经模糊不清，只知道百位和十位数字分别为2和4.

根据以上信息，解决以下问题：

(1)、情境1，问两种纸盒各做多少个，恰好将库存纸板用完?

(2)、情境2，问能否通过做适当数量的竖式和横式无盖纸盒，使得纸板的使用率为100%?请通过计算说明理由.

(3)、情境3，若本次采购的纸板裁剪做成竖式和横式无盖纸盒，并使得纸板的使用率为100%请你能帮助工厂确定丙纸板的张数.

查看试题解析

6. 根据以下素材，探索解决任务.
确定什锦糖的销售量
素材1：某商店有甲，乙两种糖果，单价分别为15元/千克，20元/千克.
素材2：商店将两种糖果混合形成A型什锦糖如图所示.小温根据个人需要，另外混合配制成B型什锦糖，每份重5千克，价格80元.
素材3：小温恰好用870元各买了若干份A，B型什锦糖.
问题解决

(1)、确定A型单价，每份什锦糖A需要多少元？

(2)、确定B型配比，每份什锦糖B中甲，乙两种糖果的质量分别是多少千克？

(3)、确定销售量，本次买卖中，商家卖出甲，乙糖果各多少千克？

查看试题解析
7. 如图，将几个小正方形与小长方形拼成一个边长为 $(a + b + c)$ 的正方形．

(1)、若用不同的方法计算这个边长为 $(a + b + c)$ 的正方形面积，就可以得到一个等式，这个等式可以为．（只要写出一个即可）；

(2)、请利用（1）中的等式解答下列问题：
①若三个实数 $a ， b ， c$ 满足 $a + b + c = 11 ， a b + b c + a c = 38$ ，求 $a^{2} + b^{2} + c^{2}$ 的值；
②若三个实数 $x ， y ， z$ 满足 $2^{x} \times 4^{y} \div 8^{z} = \frac{1}{4} ， x^{2} + 4 y^{2} + 9 z^{2} = 44$ ，求 $2 x y - 3 x z - 6 y z$ 的值．

查看试题解析
8. [阅读材料]分解因式： $x^{2} + x - 2$
解：把 $x = 1$ 代入 $x^{2} + x - 2$ ，发现此多项式的值为0，由此确定 $x^{2} + x - 2$ 中有因式 $x - 1$ ，可设 $x^{2} + x - 2 = (x - 1) (x + m) (m$ 为常数)，通过展开多项式或代入合适的 $x$ 的值即可求出 $m$ 的值.我们把这种分解因式的方法叫“试根法”.
根据以上阅读材料，完成下列问题：

(1)、请完成下列因式分解：
$x^{2} + x - 2 =$ ； $2 x^{2} - 5 x - 7 =$ ；

(2)、请你用“试根法”分解因式： $x^{3} + 3 x^{2} - 4$ ；

(3)、①若多项式 $x^{2} + m x - n (m ， n$ 为常数)分解因式后，有一个因式是 $(x - 2)$ ，求代数式 $\frac{9^{m}}{3^{n}}$ 的值；
②若多项式 $x^{4} + m x^{3} + n x - 16$ 含有因式 $(x - 2)$ 和 $(x + 1)$ ，求mn的值.

查看试题解析
9.

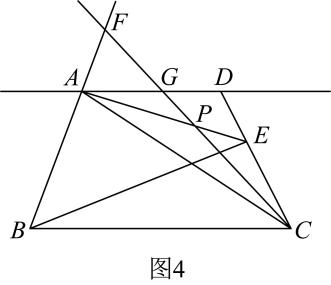
(1)、【基础巩固】
如图1，已知 $A D ∥ E F ∥ B C$ ，求证： $∠ A E B = ∠ D A E + ∠ C B E$ ；

(2)、【尝试应用】
如图2，在四边形 $A B C D$ 中， $A D ∥ B C$ ，点E是线段 $C D$ 上一点． $∠ A E B = 70 °$ ， $∠ D A E = 30 °$ ，求 $∠ C B E$ 的度数；

(3)、【拓展提高】
如图3，在四边形 $A B C D$ 中， $A D ∥ B C$ ，点E是线段 $C D$ 上一点，若 $A E$ 平分 $∠ D A C$ ， $∠ C A B = ∠ A B C$ ．

①试求出 $∠ B A E$ 的度数；

②已知 $∠ A E B = ∠ A B E$ ， $∠ E B C = 30 °$ ，点G是直线 $A D$ 上的一个动点，连接 $C G$ 并延长．

②-1若 $C A$ 恰好平分 $∠ B C D$ ，当 $C G$ 与四边形 $A B C D$ 中一边所在直线垂直时， $∠ A C G =$       ▲      ；

②-2如图4，若 $C G$ 是 $∠ A C D$ 的平分线，与 $B A$ 的延长线交于点F，与 $A E$ 交于点P，且 $∠ B F C = α °$ ，则 $∠ A D C =$       ▲       $°$ （用含 $α$ 的代数式表示）．

查看试题解析

10. 阅读以下微信群聊，完成任务．

任务一：该“旅行团”有几种打车方案？哪种方案比较划算？

任务二：小胡家的两间“亲子家庭房”共花费多少钱？

任务三：该“旅行团”分别购买了“380”和“580”这两种票价的门票各多少张？

查看试题解析

11. 对于平面直角坐标中的任意两点P，Q，若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和，则称P，Q两点为“和合点”，如图1中的P，Q两点即为“和合点”．

(1)、已知点 $A (- 4 ， 8)$ ， $B (6 ， 0)$ ， $C (6 ， 6)$ ， $D (- 2 ， 9)$ ．
①在上面四点中，与点 $E (- 5 ， - 7)$ 为“和合点”的是 ▲ ；
②若点 $F (- 3 ， 0)$ ，过点F作直线 $l ⊥ x$ 轴，点G直线l上，A、G两点为“和合点”，则点G的坐标为 ▲ ；
③若点 $M (2 a ， 3 b)$ 在第二象限，点 $N (- 3 a ， - b)$ 在第四象限，且A、M两点为“和合点”，D、N两点为“和合点”，求a，b的值．

(2)、如图2，已知点 $H (- 5 ， 0)$ ， $K (0 ， 5)$ ，点 $R (x ， y)$ 是线段 $H K$ 上的一动点，且满足 $x - y = - 5$ ，过点 $T (n ， 0)$ 作直线 $m ⊥ x$ 轴，若在直线m上存在点S，使得R，S两点为“和合点”，直接写出n的取值范围．

查看试题解析
12. 甲、乙两小区准备安装A、B两款智能快递柜，每个 $B$ 款能满足快递需求人数比 $A$ 款多20人.已知甲、乙两小区有快递需求居民分别有280人、420人.如果甲小区全部安装 $A$ 款智能快递柜，乙小区全部安装 $B$ 款智能快递柜，那么刚好满足两小区所有居民的快递需求且安装个数相同.

(1)、设每个 $A$ 款能满足快递需求人数为 $m$ 人，求 $m$ 的值.

(2)、如果甲小区安装 $A$ 款和 $B$ 款智能快递柜共7个，其中安装 $A$ 款的个数比安装 $B$ 款的2倍还多1个，分别求甲小区 $A$ 款和 $B$ 款的安装个数，并说明这样安装能否满足甲小区所有居民的快递需求.

(3)、已知购买 $A$ 款需6000元/个，购买 $B$ 款需6800元/个，请你帮助乙小区设计一个购买方案，既刚好满足乙小区所有居民的快递需求，又费用最省，并说明理由.

查看试题解析
13. 角平分线性质定理描述了角平分线上的点到角两边距离的关系，小储发现将角平分线放在三角形中，有一些新的发现，请完成下列探索过程：

(1)、【知识回顾】
如图1， $P$ 是 $∠ B O A$ 的平分线上的一点， $P E ⊥ O B$ 于点 $E$ ，作 $P D ⊥ O A$ 于点 $D$ ，试证： $P E = P D$

(2)、【深入探究】
如图2，在 $△ A B C$ 中， $B D$ 为 $∠ A B C$ 的角平分线交于 $A C$ 于 $D$ 点，其中 $A B + B C = 10 ， A D = 2 ， C D = 3$ ，求 $A B$ ．

(3)、【应用迁移】
如图3，Rt $△ A B C$ 中， $∠ C = 9 0^{∘} ， ∠ B A C$ 的角平分线 $A E$ 与 $A C$ 的中线 $B D$ 交于点 $F ， P$ 为 $C E$ 中点，连接 $P F$ ，若 $C P = 4 ， S_{△ B F P} = 20$ ，则 $A B$ 的长度为．

查看试题解析
14. 【阅读理解】
我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，解决问题的策略一般都是进行一定的转化，其中“作差法”就是常用的方法之一．作差法：就是通过作差、变形，利用差的符号确定它们的大小．即要比较代数式 $A 、 B$ 的大小，只要算 $A - B$ 的值，若 $A - B > 0$ ，则 $A > B$ ；若 $A - B = 0$ ，则 $A = B$ ；若 $A - B < 0$ ，则 $A < B$ ．

(1)、【知识运用】
请用上述方法比较下列代数式的大小（直接在空格中填写答案）：①当 $x > y$ 时， $3 x + 5 y$ $2 x + 6 y$ ；②若 $a < b < 0$ ，则 $a^{3}$ $a b^{2}$ ；

(2)、试比较 $5 x^{2} + 4 x - 3$ 与 $2 (3 x^{2} + x + 1)$ 的大小，并说明理由；

(3)、【拓展运用】
甲、乙两班同学同时从学校沿同一路线到离学校 $s (k m)$ 的研学基地参加研学．甲班有一半路程以 $v_{1} (k m / h)$ 的速度行进，另一半路程以 $v_{2} (k m / h)$ 的速度行进；乙班有一半时间以 $v_{1} (k m / h)$ 的速度行进，另一半时间以 $v_{2} (k m / h)$ 的速度行进．设甲、乙两班同学从学校到研学基地所用的时间分别为 $t_{1} (h)$ ， $t_{2} (h)$ ．
①试用含 $s$ ， $v_{1}$ ， $v_{2}$ 的代数式分别表示 $t_{1}$ 和 $t_{2}$ ，则 $t_{1} =$ ▲ ， $t_{2} =$ ▲ ．
②请你判断甲、乙两班中哪一个班的同学先到达研学基地，并说明理由．

查看试题解析
15. 如图，直线 $P Q / / M N$ ，一副三角尺 $(∠ A B C = ∠ C D E = 90 ° ， ∠ A C B = 30 ° ， ∠ B A C = 60 ° ， ∠ D C E = ∠ D E C = 45 °)$ 按如图 $①$ 放置，其中点 $E$ 在直线 $P Q$ 上，点 $B$ ， $C$ 均在直线 $M N$ 上，且 $C E$ 平分 $∠ A C N$ ．

(1)、求 $∠ D E Q$ 的度数．

(2)、如图 $②$ ，若将三角形 $A B C$ 绕点 $B$ 以每秒 $3$ 度的速度按逆时针方向旋转 $(A ， C$ 的对应点分别为 $F$ ， $G)$ ，设旋转时间为 $t (s) (0 \leq t \leq 60)$ ．
$①$ 在旋转过程中，若边 $B G / / C D$ ，求 $t$ 的值．

$②$ 若在三角形 $A B C$ 绕点 $B$ 旋转的同时，三角形 $C D E$ 绕点 $E$ 以每秒 $2$ 度的速度按顺时针方向旋转 $(C ， D$ 的对应点为 $H$ ， $K) .$ 请直接写出当边 $B G / / H K$ 时 $t$ 的值．

查看试题解析
16. 新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”，例如：方程 $x - 1 = 3$ 的解为 $x = 4$ ，而不等式组 ${\begin{array}{l} x - 1 > 1 \\ x - 2 < 3 \end{array}$ 的解集为 $2 < x < 5$ ，不难发现 $x = 4$ 在 $2 < x < 5$ 的范围内，所以方程 $x - 1 = 3$ 是不等式组 ${\begin{array}{l} x - 1 > 1 \\ x - 2 < 3 \end{array}$ 的“关联方程”．

(1)、在方程① $3 (x + 1) - x = 9$ ；② $\frac{x - 1}{2} + 1 = x$ ；③ $4 x - 7 = 0$ 中，不等式组 ${\begin{array}{l} 2 x - 2 > x - 1 \\ 3 (x - 2) - x \leq 4 \end{array}$ 的“关联方程”是；（填序号）

(2)、关于 $x$ 的方程 $2 x - k = 6$ 是不等式组 ${\begin{array}{l} \frac{3 x + 1}{2} \geq x \\ \frac{x - 1}{2} \geq \frac{2 x + 1}{3} - 1 \end{array}$ 的“关联方程”，求 $k$ 的取值范围；

(3)、若关于 $x$ 的方程 $\frac{x + 7}{2} - 3 m = 0$ 是关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x + 2 m}{2} > m \\ x - m \leq 2 m + 1 \end{array}$ 的“关联方程”，且此时不等式组有 $4$ 个整数解，试求 $m$ 的取值范围．

查看试题解析
17. 有 $7$ 个如图 $1$ 的边长分别为 $a$ ， $b$ 的小长方形，拼成如图 $2$ 的大长方形．

(1)、观察图 $2$ ，请你写出 $a$ ， $b$ 满足的等量关系（用含 $a$ 的代数式表示 $b$ ）；

(2)、将这 $7$ 个图 $1$ 的小长方形放入一个大长方形中，摆放方式如图 $3$ 所示（小长方形都呈水平或竖直摆放），图中的阴影部分分别记为Ⅰ、Ⅱ、Ⅲ．
$①$ 记阴影部分Ⅰ、Ⅱ的周长分别为 $m_{1}$ ， $m_{2}$ ，试求 $\frac{m_{1}}{m_{2}}$ 的值；

$②$ 若阴影部分Ⅰ、Ⅱ、Ⅲ的面积之和为 $86$ ，求 $a$ ， $b$ 的值．

查看试题解析
18. 甲、乙两小区准备安装A、B两款智能快递柜，每个 $B$ 款能满足快递需求人数比 $A$ 款多20人.已知甲、乙两小区有快递需求居民分别有280人、420人.如果甲小区全部安装 $A$ 款智能快递柜，乙小区全部安装 $B$ 款智能快递柜，那么刚好满足两小区所有居民的快递需求且安装个数相同.

(1)、设每个 $A$ 款能满足快递需求人数为 $m$ 人，求 $m$ 的值.

(2)、如果甲小区安装 $A$ 款和 $B$ 款智能快递柜共7个，其中安装 $A$ 款的个数比安装 $B$ 款的2倍还多1个，分别求甲小区 $A$ 款和 $B$ 款的安装个数，并说明这样安装能否满足甲小区所有居民的快递需求.

(3)、已知购买 $A$ 款需6000元/个，购买 $B$ 款需6800元/个，请你帮助乙小区设计一个购买方案，既刚好满足乙小区所有居民的快递需求，又费用最省，并说明理由.

查看试题解析
19. 佛堂古镇的万善浮桥，其夜晚的灯光秀美轮美轮，两岸景观照明还荣获了中国照明学会第十六届照明奖的一等奖.如图1所示，记浮桥两岸所在直线分别为PQ、RS，且PQ∥RS，浮桥上装有两种不同的激光灯A和激光灯B（假设PQ、RS以及由A、B两点发出的光射线始终在同一平面内）.灯A的光射线以2度每秒的速度从射线AQ顺时针旋转至射线AP后继续回转，灯B的光射线以5度每秒的速度从射线BR顺时针旋转到射线BS后也继续回转.当打开激光灯的总开关时，激光灯A和激光灯B同时开始转动.

(1)、若购买2盏灯A和4盏灯B共需10万元，购买3盏灯A和2盏灯B共需8.6万元，请问：购买灯A和灯B的单价分别是多少万元？

(2)、打开总开关，当灯A的光射线第一次从射线AQ旋转至射线AP的过程中，求灯A和灯B的光射线恰好互相垂直时所需要的时间.

(3)、如图2，打开总开关，当灯B的光射线第一次从射线BR旋转至射线BS的过程中，若灯A和灯B的光射线有交点（记为点O），延长BA至点E，作∠EAQ与∠ABO的角平分线并交于点F，求∠F与∠RBO的数量关系.

查看试题解析
20. 若一个整数能表示成 $a^{2} + b^{2}$ （a，b是整数）的形式，则称这个数为“完美数”.例如， $13 = 3^{2} + 2^{2}$ ，所以13是“完美数”，再如， $M = x^{2} + 2 x y + 2 y^{2} = (x + y)^{2} + y^{2}$ （x，y是整数），所以M也是“完美数”.

(1)、请直接写出一个小于10的“完美数”，这个“完美数”是；
判断：45（请填写“是”或“不是”）“完美数”；

(2)、已知 $S = x^{2} + 4 y^{2} - 6 x + 4 y + k$ （x，y是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由.

(3)、如果数m，n都是“完美数”， $m \neq n$ ，试说明 $\frac{(m + n)^{2} - (m - n)^{2}}{4}$ 也是“完美数”.

查看试题解析