2024年浙教版数学七(下)期末复习:填空题压轴题
试卷更新日期:2024-06-02 类型:复习试卷
一、填空题
-
1. 将一副三角板中的两块直角三角板的顶点按如图方式放在一起,其中 , , 且、、三点在同一直线上.现将三角板绕点顺时针转动度(),在转动过程中,若三角板和三角板有一组边互相平行,则转动的角度为 .
 2. 用如图中的长方形和正方形纸板作侧面和底面,做成如图的竖式和横式两种无盖纸盒现在仓库里有张正方形纸板和张长方形纸板若做了竖式纸盒个,横式纸盒个,恰好将库存的纸板用完小聪在做作业时,发现题中长方形纸板数字被墨水污染了,只记得这个数字比略大些,是 , , , , 中某个数字,则这个数字是 , 按照上述条件,最后做成的横式纸盒比竖式纸盒多个
2. 用如图中的长方形和正方形纸板作侧面和底面,做成如图的竖式和横式两种无盖纸盒现在仓库里有张正方形纸板和张长方形纸板若做了竖式纸盒个,横式纸盒个,恰好将库存的纸板用完小聪在做作业时,发现题中长方形纸板数字被墨水污染了,只记得这个数字比略大些,是 , , , , 中某个数字,则这个数字是 , 按照上述条件,最后做成的横式纸盒比竖式纸盒多个 3. 如图,数轴上的三点 , , 表示的数分别是 , , , 现以 , 为边,在数轴的同侧作正方形、正方形 . 若这两个正方形的面积和是 , 则的面积是 .
3. 如图,数轴上的三点 , , 表示的数分别是 , , , 现以 , 为边,在数轴的同侧作正方形、正方形 . 若这两个正方形的面积和是 , 则的面积是 . 4. 如图, , 射线 , 分别与 , 交于点M , N , 若 , 则的度数是 .
4. 如图, , 射线 , 分别与 , 交于点M , N , 若 , 则的度数是 . 5. 若 , , 则 .6. 如图,大长方形中放5张长为a,宽为b的相同的小长方形(各小长方形之间不重叠且不留空隙),若阴影部分面积为74,大长方形的周长为42,则小长方形的面积为 .
5. 若 , , 则 .6. 如图,大长方形中放5张长为a,宽为b的相同的小长方形(各小长方形之间不重叠且不留空隙),若阴影部分面积为74,大长方形的周长为42,则小长方形的面积为 . 7. 已知 , , 则;如图,在正方形ABCD中, , , 长方形BGLF的面积为4,其中四边形AFLJ,GCIL,KLMN均为正方形,则图中阴影部分的面积之和为 .
7. 已知 , , 则;如图,在正方形ABCD中, , , 长方形BGLF的面积为4,其中四边形AFLJ,GCIL,KLMN均为正方形,则图中阴影部分的面积之和为 . 8. 如图所示,将形状大小完全相同的“
8. 如图所示,将形状大小完全相同的“ ”按照一定规律摆成下列图形,第1幅图中“
”按照一定规律摆成下列图形,第1幅图中“ ”的个数为 , 第2幅图中“
”的个数为 , 第2幅图中“ ”的个数为 , 第3幅图中“
”的个数为 , 第3幅图中“ ”的个数为 , . 则的值为 , . 为正整数,则的值为 .
”的个数为 , . 则的值为 , . 为正整数,则的值为 .
 9. 实验室需要购买A,B,C三种型号的盒子存放材料,盒子容量和单价如下表所示:
9. 实验室需要购买A,B,C三种型号的盒子存放材料,盒子容量和单价如下表所示:盒子型号
A
B
C
盒子容量(单位:升)
2
3
4
盒子单价(单位:元)
5
6
9
其中A型号盒子做促销活动:购买3个及以上可一次性优惠4元,现有28升材料需要存放,要求每个盒子都要装满且三种盒子都至少买一个.
(1)、若购买A,B,C三种型号的盒子的个数分别为1,6,2,则购买总费用为元;(2)、若一次性购买所需盒子且购买总费用不超过58元,则购买A,B,C三种型号的盒子的个数分别为个(写出一种即可).10. 如图1是等宽的纸条,点E、F分别在上,现将纸条沿折叠成图2形状,若此时 , 再沿折叠成图3,则图3中度数为 .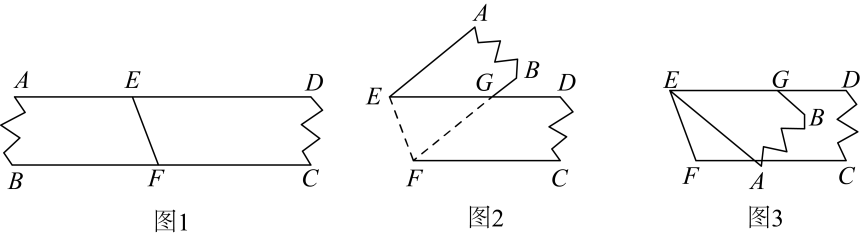 11. 已知是非负整数,且同时满足 , 则.12. 如图,在中, , 分别延长 , 至点 , 连接 , , 在取点 , 使得 , , 过点作 , 垂足为点若 , 则 .
11. 已知是非负整数,且同时满足 , 则.12. 如图,在中, , 分别延长 , 至点 , 连接 , , 在取点 , 使得 , , 过点作 , 垂足为点若 , 则 . 13. 非负数 , 满足 , 记 , 的最大值为 , 最小值 , 则 .14. 如图,把一个大长方形分割成小块,其中长方形号和号,号和号的形状和大小分别相同,号是正方形,则号的面积与大长方形的面积之比为 .
13. 非负数 , 满足 , 记 , 的最大值为 , 最小值 , 则 .14. 如图,把一个大长方形分割成小块,其中长方形号和号,号和号的形状和大小分别相同,号是正方形,则号的面积与大长方形的面积之比为 . 15. 如图,三角形纸片 , 点是边上一点,连接 , 把沿翻折,得到 , 与交于点若点是的中点, , 的面积为 , 则点、之间的距离为 .
15. 如图,三角形纸片 , 点是边上一点,连接 , 把沿翻折,得到 , 与交于点若点是的中点, , 的面积为 , 则点、之间的距离为 . 16. 现有甲,乙,丙三种糖混合而成的什锦糖50千克,其中各种糖的千克数和单价如下表.
16. 现有甲,乙,丙三种糖混合而成的什锦糖50千克,其中各种糖的千克数和单价如下表.甲种糖
乙种糖
丙种糖
千克数
20
10
20
单价(元/千克)
15
20
25
商店以糖的平均价(平均价=混合糖的总价格÷混合糖的总千克数)作为什锦糖的单价,要使什锦糖的单价每千克提高1元,则需再加入丙种糖千克.
17. 生活中我们经常用到密码,如手机解锁、密码支付等为方便记忆,有一种用“因式分解”法产生的密码,其原理是:将一个多项式分解成多个因式,如:将多项式分解结果为当时, , , 此时可得到数字密码将多项式因式分解后,利用题目中所示的方法,当时可以得到密码 , 则 .18. 已知关于 , 的方程组的解为 , 直接写出关于、的方程组的解为 .19. 现有A,B两袋糖果,其中袋中水果糖的重量占 , 其余都为奶糖,袋中奶糖的重量占 , 其余都为水果糖.将两袋糖果混合在一起,发现水果糖的重量占总重量的.(1)、当时,原来袋的重量占混合后糖果总重量的百分比为.(2)、当时,原来袋的重量占混合后糖果总重量的百分比为.20. 如果一个自然数M的个位数字不为0,且能分解成(),其中A与B都是两位数,A与B的十位数字相同,个位数字之和为6,则称数M为“如意数”,并把数M分解成的过程,称为“快乐分解”.例如,因为 , 22和24的十位数字相同,个位数字之和为6,所以528是“如意数”.(1)、最小的“如意数”是;(2)、把一个“如意数”M进行“快乐分解”,即 , A与B的和记为 , A与B的差记为 , 若能被7整除,则M的值为 .21. 用如图1所示的张长为 , 宽为()的小长方形纸片,按图的方式不重叠地放在矩形内,未被覆盖的部分(两个长方形)用阴影表示.设左上角与右下角的阴影部分的面积的差为 , 当的长度发生变化时,按照同样的放置方式,始终保持不变.则 , 之间满足的关系式为 .

