2024年浙教版数学七(下)期末复习:选择题压轴题
试卷更新日期:2024-06-02 类型:复习试卷
一、单选题
-
1. 当时,关于 , 的方程的解也是选项中方程( )的解A、 B、 C、 D、2. 设 , , , , 其中 , , 给出以下结论:
当时,;不论为何值, .
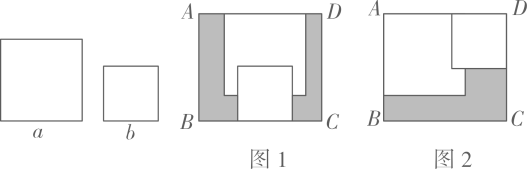
则下列判断正确的是( )
A、 , 都对 B、 , 都错 C、对,错 D、错,对3. 如图,用12块相同的长方形地板砖拼成一个矩形,设一块长方形地板砖的长和宽分别为和 , 则一块长方形地板砖的面积为( ) A、 B、 C、 D、4. 如图所示的运算程序中,如果开始输入的x的值为 , 我们发现第一次输出的结果为 , 第二次输出的结果为2,…,则第2023次输出的结果为( )
A、 B、 C、 D、4. 如图所示的运算程序中,如果开始输入的x的值为 , 我们发现第一次输出的结果为 , 第二次输出的结果为2,…,则第2023次输出的结果为( ) A、 B、2 C、 D、5. 如图,正方形内部摆放着①号,②号,③号3个边长都为1的正方形,其中②号正方形的部分被①号和③号正方形遮盖,若②号和③号正方形未被遮盖部分的面积为 , 则图中阴影部分面积为( )
A、 B、2 C、 D、5. 如图,正方形内部摆放着①号,②号,③号3个边长都为1的正方形,其中②号正方形的部分被①号和③号正方形遮盖,若②号和③号正方形未被遮盖部分的面积为 , 则图中阴影部分面积为( ) A、 B、 C、 D、6. 如图,将两张边长分别为和()的正方形纸片按图1,图2两种方式放置长方形内(图1,图2中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示,若长方形中边的长度分别为 . 设图1中阴影部分面积为 , 图2中阴影部分面积为 . 当时,的值为( )
A、 B、 C、 D、6. 如图,将两张边长分别为和()的正方形纸片按图1,图2两种方式放置长方形内(图1,图2中两张正方形纸片均有部分重叠),未被这两张正方形纸片覆盖的部分用阴影表示,若长方形中边的长度分别为 . 设图1中阴影部分面积为 , 图2中阴影部分面积为 . 当时,的值为( )
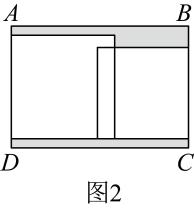 A、3b B、 C、 D、7. 如图所示,长方形中放入5张长为 , 宽为的相同的小长方形,其中 , , 三点在同一条直线上.若阴影部分的面积为38,大长方形的周长为30,则一张小长方形的面积为( )
A、3b B、 C、 D、7. 如图所示,长方形中放入5张长为 , 宽为的相同的小长方形,其中 , , 三点在同一条直线上.若阴影部分的面积为38,大长方形的周长为30,则一张小长方形的面积为( ) A、2 B、3 C、4 D、58. 如图 , 已知长方形纸带 , , , , 点、分别在边、上, , 如图 , 将纸带先沿直线折叠后,点、分别落在、的位置,如图 , 将纸带再沿折叠一次,使点落在线段上点的位置,那么的度数为( )
A、2 B、3 C、4 D、58. 如图 , 已知长方形纸带 , , , , 点、分别在边、上, , 如图 , 将纸带先沿直线折叠后,点、分别落在、的位置,如图 , 将纸带再沿折叠一次,使点落在线段上点的位置,那么的度数为( ) A、 B、 C、 D、9. 算筹是中国古代用来记数、列式和进行各种数与式演算的一种工具九章算术的“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法各行从左到右列出的算筹数分别表示未知数 , 的系数与相应的常数项把图所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 , 根据图列出的方程组为( )
A、 B、 C、 D、9. 算筹是中国古代用来记数、列式和进行各种数与式演算的一种工具九章算术的“方程”一章中介绍了一种用“算筹图”解决一次方程组的方法各行从左到右列出的算筹数分别表示未知数 , 的系数与相应的常数项把图所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 , 根据图列出的方程组为( ) A、 B、 C、 D、10. 蛟蛟和川川一起玩拼图游戏,蛟蛟将六块拼图拼成如图所示的矩形 , 其中为正方形,川川发现如果知道两块拼图的周长差,就可以知道其中一块正方形的边长了,那么这个正方形为( )
A、 B、 C、 D、10. 蛟蛟和川川一起玩拼图游戏,蛟蛟将六块拼图拼成如图所示的矩形 , 其中为正方形,川川发现如果知道两块拼图的周长差,就可以知道其中一块正方形的边长了,那么这个正方形为( ) A、 B、 C、 D、11. 如图,在长方形中,点、分别落在、上,连接得到正方形在上取一点 , 上取一点 , 使得 , 连接若 , 知道下列哪个条件,则可求正方形的面积( )
A、 B、 C、 D、11. 如图,在长方形中,点、分别落在、上,连接得到正方形在上取一点 , 上取一点 , 使得 , 连接若 , 知道下列哪个条件,则可求正方形的面积( ) A、的周长 B、的面积 C、梯形的周长 D、梯形的面积12. 如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位,得到点、、、 , 那么点的坐标为( )
A、的周长 B、的面积 C、梯形的周长 D、梯形的面积12. 如图,在平面直角坐标系中,一动点从原点出发,按向上、向右、向下、向右的方向不断地移动,每次移动一个单位,得到点、、、 , 那么点的坐标为( ) A、 B、 C、 D、13. 如图所示,将三张边长分别为a,a,b(其中 , )的正方形纸片按图甲、乙两种方式放置在长方形内(图甲,图乙中三张正方形纸片均有部分重叠),未被这三张正方形纸片覆盖的部分用阴影表示,图甲中阴影部分的周长为 , 图乙中阴影部分的周长为 , , 以下说法正确的是( )
A、 B、 C、 D、13. 如图所示,将三张边长分别为a,a,b(其中 , )的正方形纸片按图甲、乙两种方式放置在长方形内(图甲,图乙中三张正方形纸片均有部分重叠),未被这三张正方形纸片覆盖的部分用阴影表示,图甲中阴影部分的周长为 , 图乙中阴影部分的周长为 , , 以下说法正确的是( ) A、 B、 C、 D、14. 有8个形状大小相同的小球,其中一个略重些,其余7个重量相同.现给你一架天平,能将那个略重些的小球找到,则至少需要天平的次数是( )A、4 B、3 C、2 D、115. 如图,已知 , P为下方一点,G,H分别为上的点, , , ( , 且 , 均为锐角),与的角平分线交于点F,平分 , 交直线于点E,下列结论:①;②;③若 , 则 . 其中正确的序号是( ).
A、 B、 C、 D、14. 有8个形状大小相同的小球,其中一个略重些,其余7个重量相同.现给你一架天平,能将那个略重些的小球找到,则至少需要天平的次数是( )A、4 B、3 C、2 D、115. 如图,已知 , P为下方一点,G,H分别为上的点, , , ( , 且 , 均为锐角),与的角平分线交于点F,平分 , 交直线于点E,下列结论:①;②;③若 , 则 . 其中正确的序号是( ). A、①② B、②③ C、①③ D、①②③16. 中国象棋中“马走日字”(“马”从两个小方格组成的“日”字的一角走到相对的另一对角,横着走竖着走都可以),如“马”从点出发,可到达A,B,C,D,E,F中任意一点,若“马”从点P出发连续走了n次“日”字后到达点 , 则n的最小值为( )
A、①② B、②③ C、①③ D、①②③16. 中国象棋中“马走日字”(“马”从两个小方格组成的“日”字的一角走到相对的另一对角,横着走竖着走都可以),如“马”从点出发,可到达A,B,C,D,E,F中任意一点,若“马”从点P出发连续走了n次“日”字后到达点 , 则n的最小值为( )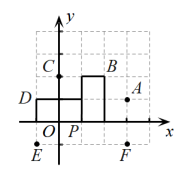 A、6 B、7 C、8 D、917. 如图, , 平分 , 的反向延长线交的平分线于点M,则与的数量关系是( )
A、6 B、7 C、8 D、917. 如图, , 平分 , 的反向延长线交的平分线于点M,则与的数量关系是( ) A、 B、 C、 D、18. 方程的整数解共有( )A、1010 B、1011 C、1012 D、202219. 已知 , , 求的值,这个问题我们可以用边长分别为和的两种正方形组成一个图形来解决,其中 , 能较为简单地解决这个问题是图形是( )A、
A、 B、 C、 D、18. 方程的整数解共有( )A、1010 B、1011 C、1012 D、202219. 已知 , , 求的值,这个问题我们可以用边长分别为和的两种正方形组成一个图形来解决,其中 , 能较为简单地解决这个问题是图形是( )A、 B、
B、 C、
C、 D、
D、 20. 已知矩形ABCD,将两张边长分别为和的正方形纸片按图1,图2两种方式放置(图1,图2两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1与图2中阴影部分的周长差为 , 若要知道的值,只需测量( )
20. 已知矩形ABCD,将两张边长分别为和的正方形纸片按图1,图2两种方式放置(图1,图2两张正方形纸片均有部分重叠),矩形中末被这两张正方形纸片覆盖的部分用阴影表示,设图1与图2中阴影部分的周长差为 , 若要知道的值,只需测量( ) A、 B、 C、BC D、AB21. 为整数,符合条件的整数的个数是( )A、1 B、2 C、4 D、522. 如图,下列选项中:①;②;③;④;⑤;⑥ , 单个选项条件可以说明的个数是( )
A、 B、 C、BC D、AB21. 为整数,符合条件的整数的个数是( )A、1 B、2 C、4 D、522. 如图,下列选项中:①;②;③;④;⑤;⑥ , 单个选项条件可以说明的个数是( ) A、2个 B、3个 C、4个 D、5个23. 若 , 则使p最接近的正整数n是( )A、4 B、5 C、6 D、724. 设 , 为实数,多项式展开后的一次项系数为 , 多项式展开后的一次项系数为:若 , 且 , 均为正整数,则( )A、与的最大值相等,与的最小值也相等 B、与的最大值相等,与的最小值不相等 C、与的最大值不相等,与的最小值相等 D、与的最大值不相等,与的最小值也不相等25. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )
A、2个 B、3个 C、4个 D、5个23. 若 , 则使p最接近的正整数n是( )A、4 B、5 C、6 D、724. 设 , 为实数,多项式展开后的一次项系数为 , 多项式展开后的一次项系数为:若 , 且 , 均为正整数,则( )A、与的最大值相等,与的最小值也相等 B、与的最大值相等,与的最小值不相等 C、与的最大值不相等,与的最小值相等 D、与的最大值不相等,与的最小值也不相等25. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺固定不动,将含角的三角尺绕顶点B顺时针转动(转动角度小于).当与三角尺的其中一条边所在的直线互相平行时,的度数是( )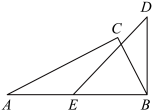 A、或或 B、或或 C、或或 D、或或26. 如图,已知 , 点E为上方一点,、分别为 , 的角平分线,若 , 则的度数为( )
A、或或 B、或或 C、或或 D、或或26. 如图,已知 , 点E为上方一点,、分别为 , 的角平分线,若 , 则的度数为( ) A、 B、 C、 D、27. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )
A、 B、 C、 D、27. 如图,将一副直角三角尺的其中两个顶点重合叠放.其中含角的三角尺ABC固定不动,将含角的三角尺DBE绕顶点顺时针转动(转动角度小于).当DE与三角尺ABC的其中一条边所在的直线互相平行时,的度数是( )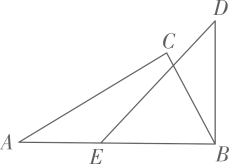 A、或或 B、或或 C、或或 D、或或
A、或或 B、或或 C、或或 D、或或