备考2024年中考数学时事热点抢分练8 环保主题
试卷更新日期：2024-06-02 类型：三轮冲刺
一、选择题
-
1. 下列环保标志中是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列环保标志，既是轴对称图形，也是中心对称图形的是（ ）A、
B、
C、
D、
3. 我国将在2060年实现碳中和，新能源、绿色能源将成为产业发展的新趋势，下列新能源环保图标中是中心对称图形的是（ ）A、
B、
C、
D、
4. 下列环保标志是轴对称图形的是（ ）A、
B、
C、
D、
5. 某无盖分类垃圾桶如右图所示，则它的俯视图是（ ）
A、
B、
C、
D、
6. 下列随手关灯、节约用水、禁止吸烟、节约用电四个环保标志中，属于轴对称图形的有几个（ ）
A、1个 B、2个 C、3个 D、4个7. 小楠所在社会实践活动小组的同学们响应“垃圾分类，从我做起”的号召，主动到附近的7个社区宣传垃圾分类.她们记录的各社区参加活动的人数如图所示，那么这组数据的众数和中位数分别是（ ）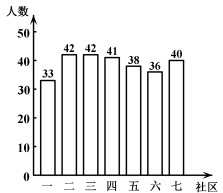
A、42，40 B、42，38 C、2，40 D、2，388. 某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多；如用新工艺，则废水排量要比环保限制的最大量少 ， 新旧工艺的废水排量之比为2：5，若设环保限制的最大量为 ， 则可列方程为（ ）A、 B、 C、 D、9. 环保人员为估计某自然保护区山雀的数量，随机捕捉了100只山雀，然后在身体某部位做好标记，放回山中，隔了一段时间之后，环保人员随机捕捉了300只山雀，发现其中5只的身体上有之前做好的标记，由此可知该自然保护区山雀的数量大约为（ ）A、6000只 B、3000只 C、5000只 D、8000只10. 为调研大众的低碳环保意识，小明在某超市出口统计后发现：一小时内使用自带环保袋的人数比使用超市塑料袋人数的2倍少4人，若使用超市塑料袋的为x人，则使用自带环保袋的人数为（ ）A、 B、 C、 D、11. 某制药厂制造一批药品，如用旧工艺，则废水排量要比环保限制的最大量还多200t；如用新工艺，则废水排量要比环保限制的最大量少100t．新、旧工艺的废水排量之比为2：5，两种工艺的废水排量各是多少？如果设新工艺的废水排量为2xt，旧工艺的废水排量为 ．那么下面所列方程正确的是（ ）A、 B、 C、 D、12. 随着生活水平的提高和环保意识的增强，小亮家购置了新能源电动汽车，这样他乘电动汽车比乘公交车上班所需的时间少用了15分钟，已知电动汽车的平均速度是公交车的2.5倍，小亮家到上班地点的距离为8千米．若设乘公交车平均每小时走x千米，则可列方程为（ ）A、 B、 C、 D、13. 垃圾分类可以把有用的垃圾回收再利用，减少了对环境的危害．随机将一节废旧的电池（有害垃圾）和矿泉水空瓶（可回收垃圾）分别放入不同的垃圾桶，则投放正确的概率为（ ）
A、 B、 C、 D、二、解答题
-
14. “保护生存环境建设美好家园”是学校开展环保类社团活动之宗旨，为了解某校全体学生参加该学校五个环保类社团项目的意愿．随机抽取了40名学生进行问卷调查，每人只能从中选择一个项目，现将问卷调查结果绘制成不完整的统计图表．
社团名称
A（环保义工）
B（绿植养护）
C（醇素制作）
D（回收材料）
E（垃圾分类）
人数
4
m
16
n
4
请你根据以上信息解答下列问题：
(1)、填空：m＝；扇形统计图中D（回收材料）部分扇形的圆心角等于 度；(2)、请补全条形统计图：若该校有2400名学生，估计全校约有多少名学生意愿参加回收材料社团．(3)、请用树状图或列表法求随机抽取该校两名同学选择环保类同一社团项目的概率．15. 自我国实施“限塑令”起，开始有偿使用环保购物袋，为了满足市场需求，某厂家生产A ， B两种款式的环保购物袋，每天生产6000个，两种购物袋的成本和售价如下表，若设每天生产A种购物袋x个．成本（元/个）
售价（元/个）
A
2
2.5
B
3
3.6
(1)、用含x的整式表示每天生产的环保购物袋的总成本，并进行化简；(2)、用含x的整式表示每天获得的总利润，并进行化简（利润=售价-成本）；(3)、当时，求每天生产的总成本与每天获得的总利润．16. 在国家积极政策的鼓励下，环保意识日渐深入人心，新能源汽车的市场需求逐年上升．(1)、某汽车企业2020年到2022年这两年新能源汽车的销售总量增长了96%．求该汽车企业这两年新能源汽车销售总量的平均年增长率；(2)、某汽车企业下属的一个专卖店经销一款进价为15万元/辆的新能源汽车，经销一段时间后发现：当该款汽车售价定为25万元/辆时，平均每周售出8辆；售价每降低0.5万元，平均每周多售出1辆．若该店计划下调售价使平均每周的销售利润为96万元，并且尽量让利于顾客，求下调后每辆汽车的售价．17. “低碳生活，绿色出行”是一种环保、健康的生活方式，小丽从甲地匀速步行前往乙地，同时，小明从乙地沿同一路线匀速步行前往甲地，两人之间的距离y（m）与步行时间x（min）之间的函数关系式如图中折线段AB-BC-CD所示．
(1)、小丽与小明出发min相遇；(2)、在步行过程中，若小明先到达甲地．①求小丽和小明步行的速度各是多少？
②计算出点C的坐标，并解释点C的实际意义．
18. 环保是当今社会人们最关注的话题之一，某校为了解碳中和、食品安全等知识的普及情况，随机抽取了部分学生进行问卷调查，问卷有四个选项（每位被调查的学生必须且只能选一项）：A．不了解；B．了解较少；C．了解；D．非常了解．并将调查结果绘制成了以下两幅不完整的统计图．
请根据统计图，回答下列问题．
(1)、本次共抽取了 ▲名学生，并根据调查信息补全条形统计图．(2)、若该校共有1600名学生，估计“非常了解”的学生共有名．(3)、在被调查的“非常了解”的学生中，有四名学生（2名男生和2名女生）来自九（1）班，班主任想从这四名学生中任选两名去参加环保知识竞赛．请你用列表法或画树状图法，求出被选中的两人恰好是一男一女的概率．19. 随着《某市生活垃圾分类管理条例》正式实施，某市垃圾分类工作进入强制实施阶段，某小区物业管理负责人提出了购买分类垃圾桶的方案．方案一：买A型号分类垃圾桶，需要费用2500元，以后每月的垃圾处理费用为300元；
方案二：买B型号分类垃圾桶，需要费用1500元，以后每月的垃圾处理费用为400元；设缴费时长为x个月，方案一和方案二的购买费和垃圾处理费的和分别为M元、N元．
(1)、 ， （分别用含x的式子表示）．(2)、若缴费时长为12个月，则哪种方案的费用更少？并说明理由．(3)、当缴费时长为多少个月时，两种方案的费用相同？20. 某学校在宣传垃圾分类的实践活动中，需印制主题为“做文明有礼中学生，垃圾分类从我做起”的宣传单，其附近两家图文社印制此种宣传单的收费标准如图所示：
(1)、为达到及时宣传的目的，学校同时在、两家图文社共印制了张宣传单，印制费用共计元，学校在、两家图文社各印制了多少张宣传单(2)、次月，为扩大宣传，学校计划选择家图文社加印一部分宣传单，在印制费用不超过元的前提下，最多可以印制多少张宣传单三、综合题
-
21. 现如今，环保这一理念越来越融入到我们的生活中．为了加强学生的环保意识，某中学举办我是环保小达人的演讲比赛，比赛分为入围赛和决赛两个赛段．全校学生积极响应，全部报名参加入围赛，随机抽取了若干名学生，调查他们每天课后练习演讲的时间，现将调查结果绘制成如下尚不完整的统计图表．请根据统计图表提供的信息，回答下列问题：
组别
练习时间（分钟）
频数（人）
百分比
(1)、将下面的统计表和条形统计图补充完整；(2)、若该校学生有人，请你估计每天课后练习时间超过分钟的学生有多少人？(3)、演讲决赛时，总成绩由内容、表达、风度、印象四部分组成，并按计算．进入冠亚军争夺的张明和赵亮的各项得分如下表：内容
表达
风度
印象
张明
分
分
分
分
赵亮
分
分
分
分
总成绩高的人为冠军，请你通过计算判断他俩谁获得冠军？
22. 低碳生活已是如今社会的一种潮流形式，人们的环保观念也在逐渐加深．低碳环保，绿色出行成为大家的生活理念，不少人选择自行车出行．某公司销售甲、乙两种型号的自行车，其中甲型自行车进货价格为每台元，乙型自行车进货价格为每台元．该公司销售台甲型自行车和台乙型自行车，可获利元，销售台甲型自行车和台乙型自行车，可获利元．(1)、该公司销售一台甲型、一台乙型自行车的利润各是多少元？(2)、为满足大众需求，该公司准备加购甲、乙两种型号的自行车共台，且资金不超过元，最少需要购买甲型自行车多少台？23. “绿色出行，低碳环保”，共享电动车是一种新理念下的交通工具，现有甲、乙两种品牌的共享电动车，收费标准y（元）与骑行时间x（分）之间的函数关系如图所示，请根据图象信息，解答下列问题：
(1)、甲品牌共享电动车每分钟收费元．(2)、当骑行时间不低于10分钟时，求乙品牌共享电动车y与x之间的函数关系式．(3)、已知两种品牌共享电动车的平均行驶速度均为 ， 若小明需要骑行共享电动车去上班，小明家到单位的距离为 ， 请通过计算帮小明选择哪个品牌的共享电动车更省钱．24. 根据《环境空气质量指数（）技术规定（试行）》规定：空气污染指数划分为六档，对应于空气质量的六个级别，指数越大，级别越高，说明污染越严重，对人体健康的影响也越明显.当空气污染指数达到0～50时为一级；51～100时为二级，101～150时为三级；151～200时为四级；201～300时为五级，空气污染指数大于300，空气质量级别为六级，其中一级属于优，二级属于良，三级属于轻度污染，四级属于中度污染，五级属于重度污染，六级为严重污染．某校数学兴趣小组随机抽取了2023年1—6月份所在城市某些天的空气质量检测数据，并绘制成如下图、表：级别
指数
天数
频率
一级
0～50
8
0.16
二级
51～100
20
0.4
三级
101～150
0.3
四级
151～200
5
五级
201～300
1
0.02
六级
大于300
1
0.02
请根据以上图、表提供的信息，解答下列问题：
(1)、统计表中的 ▲ ， ▲ ；并补全条形统计图；(2)、根据以上数据的分析，请你估计2023年该城市全年的空气污染指数属于轻度污染和中度污染的大概共有多少天？（一年按365天计算）25. 空气质量指数（Air Quality Index，缩写AQI）是定量描述空气状况的非线性无量纲指数．其数值越大、级别和类别越高，说明空气污染状况越严重，对人体的健康危害也就越大，适用于表示某地区的短期空气质量状况和变化趋势．（空气污染指数为0~50是优；空气污染指数为50~100是良好；空气污染指数为100~150是轻度污染；空气污染指数为150~200是中度污染；空气污染指数为200~250是重度污染．）如图表示的是某地区2022年11月份30天日均AQI指数的频率分布直方图．
空气质量指数（AQI）
0~50
50~100
100~150
150~200
200~250
天数
3
3
3
频率
0.1
0.1
0.1
（注：每组数据可含最高值，不含最低值）
(1)、请你根据上述频率分布直方图及表格完成下面的填空：这个地区11月份空气为轻度污染的天数是天．；；； ．
(2)、为了进一步改善生活环境和空气质量，提高人民的生活质量，当地政府计划从2023年开始增加绿化面积．已知2022年底该地区的绿化面积为20万亩，如果到2024年底，该地区的绿化面积比为2022年的绿化面积增加了50%，假设这两年绿化面积的年增长率相同，求这两年中绿化面积每年的增长率（精确到0.01）（参考数据： ， ， ， ）26. 为了“天更蓝，水更绿”，其市政府加大了对空气污染的治理力度，经过几年的努力，空气质量明显改善，现收集了该市连续30天的空气质量情况作为样本，整理并制作了如下表格和一幅不完整的条形统计图．空气污染指数（）
30
40
70
80
90
110
120
140
天数（t）
1
2
a
5
7
6
b
2
说明：环境空气质量指数技术（AQI）规定：时，空气质量为优；时，空气质量为良；时，空气质量为轻度污染；时，空气质量为中度污染…
根据上述信息，解答下列问题：
(1)、表格中 ， ， 空气污染指数这组数据的众数 ， 中位数；(2)、请补全空气质量天数条形统计图；(3)、根据已完成的条形统计图，制作相应的扇形统计图，写出必要的过程；(4)、健康专家温馨提示：空气污染指数在100以下适合做户外运动．请根据以上信息，估计该市居民一年（以365天计）中有多少天适合做户外运动？