2024年北师大版数学八(下)微素养核心突破13 多边形的内角与外角和
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 一个多边形的内角和为360°,则这个多边形是( )A、三角形 B、四边形 C、五边形 D、六边形2. 若一个多边形的内角和比它的外角和大 , 则该多边形的边数为( )A、 B、 C、 D、3. 正多边形的一个外角的度数为 , 则这个正多边形的边数为( )A、12 B、10 C、8 D、64. 若一个多边形的内角和等于900°,则这个多边形的边数是( )A、8 B、7 C、6 D、55. 一个六边形如图所示.已知 . 若 , 则的值为( )
 A、 B、 C、 D、6. 一个六边形的内角和等于( )A、360° B、480° C、720° D、1080°7. 如图,小明从A点出发,沿直线前进16米后向左转45°,又向左转45°,…,照这样走下去,共走路程为( )
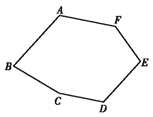
A、 B、 C、 D、6. 一个六边形的内角和等于( )A、360° B、480° C、720° D、1080°7. 如图,小明从A点出发,沿直线前进16米后向左转45°,又向左转45°,…,照这样走下去,共走路程为( )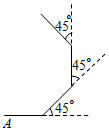 A、96米 B、128米 C、160米 D、192米8. 如图,点A、B、C、D、E、F在同一平面内,连接、、、、、 , 若 , 则等于( )
A、96米 B、128米 C、160米 D、192米8. 如图,点A、B、C、D、E、F在同一平面内,连接、、、、、 , 若 , 则等于( ) A、 B、 C、 D、9. 下列说法正确的是( )A、五边形的内角和是720° B、有两边相等的两个直角三角形全等 C、若关于 的方程 有增根,则 D、若关于 的不等式 恰有2个正整数解,则 的最大值是410. 如图,在四边形纸片中, , 将纸片折叠,使点C、D落在边上的点处,折痕为 , 则( )
A、 B、 C、 D、9. 下列说法正确的是( )A、五边形的内角和是720° B、有两边相等的两个直角三角形全等 C、若关于 的方程 有增根,则 D、若关于 的不等式 恰有2个正整数解,则 的最大值是410. 如图,在四边形纸片中, , 将纸片折叠,使点C、D落在边上的点处,折痕为 , 则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 一个正多边形的内角和为 , 则这个正多边形的每一个外角等于度.12. 一个多边形的内角和与它的外角和之比为 , 则这个多边形的边数是 .13. 正八边形每个外角的度数为 .14. 一个多边形所有的内角与它所有的外角之和是 , 过这个多边形的一个顶点可画出条对角线.15. 编程兴趣小组为半径为0.2米的圆形扫地机器人编制了如图所示的程序,若扫地机器人在无障碍的实验室平地上按照编制的程序扫地,则这个扫地机器人扫过的实验室平地的面积是米 .

三、解答题
-
16. 某科技小组制作了一个机器人,它能根据指令要求进行行进和旋转,某一指令规定:机器人先向前方行走2 m,然后左转60°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了多少米?17. , ,且 , ,求 和 的度数.
 18. 探究与发现:
18. 探究与发现: (1)、如图1,在中, , 分别平分和 .
(1)、如图1,在中, , 分别平分和 .①若 , 则;
②若 , 用含有的式子表示的度数为;
(2)、如图2,在四边形中, , 分别平分和 , 试探究与的数量关系,并说明理由;(3)、如图3,在六边形中, , 分别平分和 , 请直接写出与的数量关系.19. 利用“模型”解决几何综合问题往往会取得事半功倍的效果.
几何模型:如图(1),我们称它为“A”型图案,
易证明:;
应用上面模型解决问题:
(1)、如图(2),“五角星”形,求?分析:图中是“A”型图,于是 , 所以;
(2)、如图(3),“七角星”形,求;(3)、如图(4),“八角星”形,可以求得:;