2024年北师大版数学八(下)微素养核心突破12 三角形的中位线
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 如图,某校综合实践小组为测量校内人工湖的宽度 , 在岸边选一点 , 并分别找到和的中点 , 测得米,则人工湖的宽度为( )
 A、30米 B、32米 C、36米 D、48米2. 如图,在平行四边形ABCD中, , E为上一动点,M,N分别为的中点,则的长为( )
A、30米 B、32米 C、36米 D、48米2. 如图,在平行四边形ABCD中, , E为上一动点,M,N分别为的中点,则的长为( ) A、2 B、3 C、4 D、不确定3. 如图,在中, , 点、分别是、的中点,则的长为( )
A、2 B、3 C、4 D、不确定3. 如图,在中, , 点、分别是、的中点,则的长为( ) A、1 B、2 C、3 D、44. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, ,则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( )
A、1 B、2 C、3 D、44. 如图,平行四边形ABCD的对角线AC、BD相交于点O,AE平分∠BAD,分别交BC、BD于点E、P,连接OE,∠ADC=60°, ,则下列结论:①∠CAD=30° ② ③S平行四边形ABCD=AB•AC ④ ,正确的个数是( ) A、1 B、2 C、3 D、45. 如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )
A、1 B、2 C、3 D、45. 如图,在四边形ABCD中,AB=CD,M,N,P分别是AD,BC,BD的中点,若∠MPN=130°,则∠NMP的度数为( )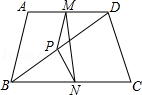 A、10° B、15° C、25° D、40°6. 如图,在中,分别是的中点.若 , 四边形的周长是( )
A、10° B、15° C、25° D、40°6. 如图,在中,分别是的中点.若 , 四边形的周长是( ) A、28 B、14 C、10 D、77. 如图,的周长是24,点D、E在边上,的平分线垂直于 , 垂足为点Q,的平分线垂直于 , 垂足为点P,若 , 则的长为( )
A、28 B、14 C、10 D、77. 如图,的周长是24,点D、E在边上,的平分线垂直于 , 垂足为点Q,的平分线垂直于 , 垂足为点P,若 , 则的长为( ) A、5 B、4 C、2 D、38. 如图,平行四边形ABCD的对角线交于点O,且 , 过点O作 , 交AD于点M,如果的周长为6,那么平行四边形ABCD的周长是( )
A、5 B、4 C、2 D、38. 如图,平行四边形ABCD的对角线交于点O,且 , 过点O作 , 交AD于点M,如果的周长为6,那么平行四边形ABCD的周长是( ) A、12 B、15 C、18 D、209. 如图,已知在中, , 是边上的中线.按下列步骤作图:①分别以点为圆心,大于线段长度一半的长为半径作弧,相交于点;②过点作直线 , 分别交 , 于点;③连结 . 则下列结论错误的是( )
A、12 B、15 C、18 D、209. 如图,已知在中, , 是边上的中线.按下列步骤作图:①分别以点为圆心,大于线段长度一半的长为半径作弧,相交于点;②过点作直线 , 分别交 , 于点;③连结 . 则下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4嗯,共24分)
-
10. 如图,在周长为600米的三角形地块中修建如图所示的三条水渠,则水渠的总长为 . 米.
 11. 如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点连结EF,FM,则FM= , 线段EF的最大值为
11. 如图,在四边形ABCD中,AB=2,CD=6,E,F,M分别为边BC,AD和对角线BD的中点连结EF,FM,则FM= , 线段EF的最大值为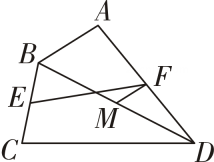 12. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为.
12. 如图,已知△ABC中,点M是BC边上的中点,AN平分∠BAC,BN⊥AN于点N,若AB=8,MN=2,则AC的长为. 13. 四边形中,对角线 , , 点分别是的中点,连接 , 取中点 , 连接 , 则的值为 .
13. 四边形中,对角线 , , 点分别是的中点,连接 , 取中点 , 连接 , 则的值为 .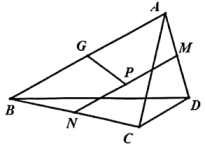 14. 如图,在平行四边形中, , , 将沿翻折至 , 连接当长为 时,是直角三角形.
14. 如图,在平行四边形中, , , 将沿翻折至 , 连接当长为 时,是直角三角形.
三、作图题(共8分)
-
15. 如图,在7×7网格中,
线段AB的两个端点和点C都在网格的格点上,分别按下列要求仅用无刻度直尺画图(保留作图痕迹)。
 (1)、在图甲中画线段AB的中点M。(2)、在图乙中画线段CD,使得CD= AB
(1)、在图甲中画线段AB的中点M。(2)、在图乙中画线段CD,使得CD= AB四、解答题(共6题,共58分)
-
16. 如图所示,在△ABC中,点D,E分别为AB,AC的中点,点H在线段CE上,连结BH,点G,F分别为BH,CH的中点.
 (1)、求证:四边形DEFG为平行四边形;(2)、DG⊥BH,BD=3,EF=2,求线段BG的长度.17. 如图,已知G、H是△ABC的边AC的三等分点,GE∥BH , 交AB于点E , HF∥BG交BC于点F , 延长EG、FH交于点D , 连接AD、DC , 设AC和BD交于点O , 求证:四边形ABCD是平行四边形.
(1)、求证:四边形DEFG为平行四边形;(2)、DG⊥BH,BD=3,EF=2,求线段BG的长度.17. 如图,已知G、H是△ABC的边AC的三等分点,GE∥BH , 交AB于点E , HF∥BG交BC于点F , 延长EG、FH交于点D , 连接AD、DC , 设AC和BD交于点O , 求证:四边形ABCD是平行四边形. 18. 如图,等边的边长是分别为的中点,延长至点 , 使 , 连接和 .
18. 如图,等边的边长是分别为的中点,延长至点 , 使 , 连接和 . (1)、求证:四边形是平行四边形;(2)、求的长.19. 如图,在矩形中, , , 点E为中点,连接 , 点F为中点,点G为线段上一点,连接 .
(1)、求证:四边形是平行四边形;(2)、求的长.19. 如图,在矩形中, , , 点E为中点,连接 , 点F为中点,点G为线段上一点,连接 . (1)、如图1,若点G为中点,求证:四边形为平行四边形;(2)、如图2,若点G使得 , 求四边形的面积;(3)、如图3,连接 , 若点G使得 , 求的长.20. 如图1,平面直角坐标中,O为坐标原点,点A、C都在坐标轴上, , 连接 , , 矩形的面积是60.
(1)、如图1,若点G为中点,求证:四边形为平行四边形;(2)、如图2,若点G使得 , 求四边形的面积;(3)、如图3,连接 , 若点G使得 , 求的长.20. 如图1,平面直角坐标中,O为坐标原点,点A、C都在坐标轴上, , 连接 , , 矩形的面积是60. (1)、求点B坐标;(2)、如图2,点E、F分别在线段、上, , 连接 , 当四边形是平行四边形时,求点F坐标;(3)、如图3,在(2)的条件下,点Q在的延长线上,连接 , 点M是的中点,连接、、 , 点N在上,连接 , , 连接并延长交y轴于点P,连接 , 当时,求点N坐标.21. 已知点O是△ABC内任意一点,连接OA并延长到点E , 使得AE=OA , 以OB , OC为邻边作平行四边形OBFC , 连接OF , 与BC交于点H , 连接EF .
(1)、求点B坐标;(2)、如图2,点E、F分别在线段、上, , 连接 , 当四边形是平行四边形时,求点F坐标;(3)、如图3,在(2)的条件下,点Q在的延长线上,连接 , 点M是的中点,连接、、 , 点N在上,连接 , , 连接并延长交y轴于点P,连接 , 当时,求点N坐标.21. 已知点O是△ABC内任意一点,连接OA并延长到点E , 使得AE=OA , 以OB , OC为邻边作平行四边形OBFC , 连接OF , 与BC交于点H , 连接EF . (1)、问题发现
(1)、问题发现如图1,若△ABC为等边三角形,线段EF与BC的位置关系是 , 数量关系为 ;
(2)、拓展探究如图2,若△ABC为等腰直角三角形(BC为斜边),(1)中的两个结论是否成立?若成立,请给予证明;若不成立,请写出正确的结论再给予证明;
(3)、解决问题如图3,若△ABC是等腰三角形,AB=AC=2,BC=3,请你直接写出线段EF的长.
-