2024年北师大版数学八(下)微素养核心突破11 平行四边形中的分类讨论问题
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 在中, , 平分交于点E , 若点E分为两部分,则的长为( )A、1 B、1或9 C、4 D、4或122. 在平行四边形ABCD中有一个内角为50°,则∠A的度数为( )A、50° B、100° C、50°或100° D、50°或130°3. 在 中, 、 分别是 和 的平分线, 、 分别与 相交于点 、 , , ,则 的长为( )A、10 B、14 C、8或14 D、10或144. 将一个四边形 的纸片剪去一个三角形,则剩下图形的内角和为( ).A、180° B、180°或360° C、360°或540° D、180°或360°或540°5. 在平面直角坐标系中,O为坐标原点,已知点A,B的坐标分别是(2,0),(4,2),若在x轴下方有一点P,使以O,A,P为顶点的三角形与△OAB全等,则满足条件的P点的坐标是( )A、(4,﹣2) B、(﹣4,﹣2) C、(4,﹣2)或(﹣2,﹣2) D、(4,﹣2)或(﹣4,﹣2)6. 如图,在平面直角坐标系中,A(-8,-1),B(-6,-9),C(-2,-9),D(-4,-1)先将四边形ABCD沿x轴翻折,再向右平移8个单位长度,向下平移1个单位长度后,得到四边形A1B1C1D1 , 最后将四边形A1B1C1D1 , 绕着A1旋转,使旋转后的四边形对角线的交点落在x轴上,则旋转后的四边形对角线交点坐标为( )
 A、(4 ,0) B、(5,0) C、(4,0)或 (5,0) D、(5,0)或(-5,0)7. 如图,四边形中,AD//BC, , M是上一点,且 , 点E从点A出发以的速度向点D运动,点F从点C出发,以的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为 , 则当以A、M、E、F为顶点的四边形是平行四边形时,t的值是( )
A、(4 ,0) B、(5,0) C、(4,0)或 (5,0) D、(5,0)或(-5,0)7. 如图,四边形中,AD//BC, , M是上一点,且 , 点E从点A出发以的速度向点D运动,点F从点C出发,以的速度向点B运动,当其中一点到达终点,另一点也随之停止,设运动时间为 , 则当以A、M、E、F为顶点的四边形是平行四边形时,t的值是( ) A、 B、3 C、3或 D、或8. 平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为( )cmA、14 B、16 C、12或14 D、14或169. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或10. 如图,已知平行四边形ABCD, , , ,点P是边AB上一动点,作 于点E,作 (PF在PE右边)且始终保持 ,连接CF、DF,设 ,则m满足( )
A、 B、3 C、3或 D、或8. 平行四边形的一个内角平分线将该平行四边形的一边分为2cm和3cm两部分,则该平行四边形的周长为( )cmA、14 B、16 C、12或14 D、14或169. 在面积为的平行四边形ABCD中,分别过点A作直线BC的垂线AE,垂足为E,作直线CD的垂线AF,垂足为F.若AB= , BC= , 则CE+CF的值为( )A、 B、 C、或 D、或10. 如图,已知平行四边形ABCD, , , ,点P是边AB上一动点,作 于点E,作 (PF在PE右边)且始终保持 ,连接CF、DF,设 ,则m满足( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共20分)
-
11. 在平面直角坐标系中,点为坐标原点,已知点 , 点 , 在平面直角坐标系中求点 , 使得以点四点为顶点的四边形为平行四边形,请写出满足条件的点的坐标: .12. 如图所示,在▱ABCD中,对角线交于点O,点E,F在对角线AC上(不同于点A,C),当点E,F的位置满足的条件时,四边形DEBF是平行四边形。
 13. 在平面直角坐标系中,点A、B、C的坐标分别是 , , ,若以点A、B、C、D为顶点的四边形是平行四边形,则满足条件的D点共有个.14. 在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .15. 如图,等腰三角形纸片ABC中,于点D , , , 沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形较长对角线的长为.
13. 在平面直角坐标系中,点A、B、C的坐标分别是 , , ,若以点A、B、C、D为顶点的四边形是平行四边形,则满足条件的D点共有个.14. 在平行四边形 中, 平分 交边 于 , 平分 交边 于 .若 , ,则 .15. 如图,等腰三角形纸片ABC中,于点D , , , 沿AD剪成两个三角形.用这两个三角形拼成平行四边形,该平行四边形较长对角线的长为.
三、解答题(共7题,共70分)
-
16. 如图,在平面直角坐标系中,四边形ABCD是平行四边形,A(-3,0),B(3,0) ,C(0,4),连结OD,点E是线段0D的中点.
 (1)、求点E和点D的坐标.(2)、平面内是否存在一点N,使以C,D,E,N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.17. 在平面直角坐标系中,对于点 , 给出如下定义:当点满足时,称点Q是点P的等积点.已知点 .
(1)、求点E和点D的坐标.(2)、平面内是否存在一点N,使以C,D,E,N为顶点的四边形是平行四边形?若存在,请求出点N的坐标;若不存在,请说明理由.17. 在平面直角坐标系中,对于点 , 给出如下定义:当点满足时,称点Q是点P的等积点.已知点 . (1)、在 , , 中,点P的等积点是 .(2)、点Q是P点的等积点,点C在x轴上,以O,P,Q,C为顶点的四边形是平行四边形,求点C的坐标.18. 如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向以4cm/s的速度运动,当点M运动到点D时,点N随之停止运动,设运动时间为t(s),
(1)、在 , , 中,点P的等积点是 .(2)、点Q是P点的等积点,点C在x轴上,以O,P,Q,C为顶点的四边形是平行四边形,求点C的坐标.18. 如图,在平行四边形ABCD中,AD=2AB=6cm,BE是∠ABC的角平分线,点M从点E出发,沿ED方向以1cm/s的速度向点D运动,点N从点C出发,沿射线CB方向以4cm/s的速度运动,当点M运动到点D时,点N随之停止运动,设运动时间为t(s), (1)、求AE的长;(2)、是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.(3)、当时,线段NM将平行四边形ABCD面积二等分(直接写出答案)”19. 如图,在平面直角坐标系中,已知直线交x轴于点A,交y轴于点 , 过点C作直线交x轴于点B,且 , , 点P在线段上,P的坐标为 .
(1)、求AE的长;(2)、是否存在以M、E、B、N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.(3)、当时,线段NM将平行四边形ABCD面积二等分(直接写出答案)”19. 如图,在平面直角坐标系中,已知直线交x轴于点A,交y轴于点 , 过点C作直线交x轴于点B,且 , , 点P在线段上,P的坐标为 . (1)、求的长;(2)、若M为线段的中点,求直线的解析式;(3)、在平面内是否存在点Q,使以点A、C、P、Q为顶点的四边形是平行四边形?若存在请直接写出点Q的坐标;若不存在请说明理由.20. 综合与探究
(1)、求的长;(2)、若M为线段的中点,求直线的解析式;(3)、在平面内是否存在点Q,使以点A、C、P、Q为顶点的四边形是平行四边形?若存在请直接写出点Q的坐标;若不存在请说明理由.20. 综合与探究如图,直线分别交轴,轴于点 , 过点A作直线分别交轴,轴于点 , .
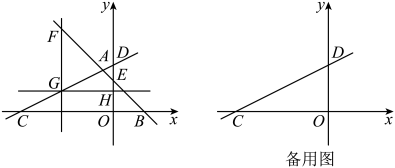 (1)、求直线的解析式.(2)、在轴左侧作直线轴,分别交直线 , 于点 . 当时,过点作直线轴,交轴于点 . 能否在直线上找一点 , 使的值最小,求出点的坐标.(3)、为直线上一点,在(2)的条件下,轴上是否存在点使得以为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.21. 问题:如图,在平行四边形中, , 的平分线分别与直线交于点E、F.
(1)、求直线的解析式.(2)、在轴左侧作直线轴,分别交直线 , 于点 . 当时,过点作直线轴,交轴于点 . 能否在直线上找一点 , 使的值最小,求出点的坐标.(3)、为直线上一点,在(2)的条件下,轴上是否存在点使得以为顶点的四边形为平行四边形?若存在,请直接写出点的坐标;若不存在,请说明理由.21. 问题:如图,在平行四边形中, , 的平分线分别与直线交于点E、F. (1)、请直接写出的长.(2)、探究:把“问题”中的条件“”去掉,其余条件不变.
(1)、请直接写出的长.(2)、探究:把“问题”中的条件“”去掉,其余条件不变.①当点E与点F重合时,的长为 .
②当点E与点C重合时,的长为 .
(3)、把“问题”中的条件“”去掉,其余条件不变,当点C , D , E , F相邻两点间的距离相等时,求的值.22. 如图,在平面直角坐标系中,点 , 点 , 点 , 以、为边作 , 点E为中点,连接、 . (1)、分别求出线段和线段所在直线解析式;(2)、点P为线段上的一个动点,作点B关于点P的中心对称点F,设点P横坐标为a,用含a的代数式表示点F的坐标(不用写出a的取值范围);(3)、在(2)的条件下,
(1)、分别求出线段和线段所在直线解析式;(2)、点P为线段上的一个动点,作点B关于点P的中心对称点F,设点P横坐标为a,用含a的代数式表示点F的坐标(不用写出a的取值范围);(3)、在(2)的条件下,①当点F移动到的边上时,求点P坐标;
②M为中点,N为中点,连接、 . 请利用备用图探究,直接写出在点P的运动过程中,周长的最小值和此时点P的坐标.