2024年北师大版数学八(下)微素养核心突破10 平行四边形的折叠问题
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 如图,将平行四边形ABCD沿对角线BD折叠,使点A落在E处.若∠1=56°,∠2=42°则∠A的度数为( )
 A、108° B、109° C、110° D、111°2. 如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为
A、108° B、109° C、110° D、111°2. 如图,将▱ABCD沿对角线BD折叠,使点A落在点E处,交BC于点F,若∠ABD=48°,∠CFD=40°,则∠E为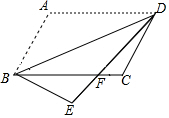 A、 B、 C、 D、3. 如图,在中,将沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , 则的周长为( )
A、 B、 C、 D、3. 如图,在中,将沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , 则的周长为( ) A、24 B、22 C、16 D、124. 如图,在中,将沿折叠后,点D恰好落在的延长线上的点E处.若 , , 则的周长为( )
A、24 B、22 C、16 D、124. 如图,在中,将沿折叠后,点D恰好落在的延长线上的点E处.若 , , 则的周长为( ) A、6 B、9 C、12 D、155. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A、6 B、9 C、12 D、155. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( ) A、66° B、104° C、114° D、124°6. 如图,已知在中,点是边上一点,将沿翻折,点正好落在边上的点处,若的周长为 , 的周长为 , 则的长为( )
A、66° B、104° C、114° D、124°6. 如图,已知在中,点是边上一点,将沿翻折,点正好落在边上的点处,若的周长为 , 的周长为 , 则的长为( ) A、6cm B、7cm C、10cm D、12cm7. 如图,在平行四边形ABCD中, , DF=6,E为AC上一点,将沿着DE翻折,点A恰好落在边CD上的F点处,连接BF,则BF长度为 ( ).
A、6cm B、7cm C、10cm D、12cm7. 如图,在平行四边形ABCD中, , DF=6,E为AC上一点,将沿着DE翻折,点A恰好落在边CD上的F点处,连接BF,则BF长度为 ( ). A、 B、 C、 D、+28. 2022北京冬奥会的设计呈现了中国美学,很多设计中利用了轴对称的美.如图,在平行四边形纸片ABCD中,对角线AC与BD相交于点E, , , 李旻老师设计时将平行四边形纸片ABCD沿对角线AC折叠,使得点B落在点的位置,连接 , 则的长为( )
A、 B、 C、 D、+28. 2022北京冬奥会的设计呈现了中国美学,很多设计中利用了轴对称的美.如图,在平行四边形纸片ABCD中,对角线AC与BD相交于点E, , , 李旻老师设计时将平行四边形纸片ABCD沿对角线AC折叠,使得点B落在点的位置,连接 , 则的长为( ) A、 B、 C、 D、159. 如图,AC是▱ABCD的对角线,将▱ABCD折叠,使得点A与点C重合,再将其打开展平,得折痕EF,EF与AC交于点O,G为CF的中点,连接OG、CE.则下列结论:①;②;③;④ . 其中正确的有( )
A、 B、 C、 D、159. 如图,AC是▱ABCD的对角线,将▱ABCD折叠,使得点A与点C重合,再将其打开展平,得折痕EF,EF与AC交于点O,G为CF的中点,连接OG、CE.则下列结论:①;②;③;④ . 其中正确的有( ) A、4个 B、3个 C、2个 D、1个10. 如图,在平面直角坐标系中,四边形OABC是平行四边形,且顶点的坐标为 , 点的坐标为 , 将平行四边形OABC沿着直线OC翻折,得到四边形 , 若直线把六边形的面积分成相等的两部分,则直线的解析式为( )
A、4个 B、3个 C、2个 D、1个10. 如图,在平面直角坐标系中,四边形OABC是平行四边形,且顶点的坐标为 , 点的坐标为 , 将平行四边形OABC沿着直线OC翻折,得到四边形 , 若直线把六边形的面积分成相等的两部分,则直线的解析式为( ) A、或 B、或 C、或 D、或
A、或 B、或 C、或 D、或二、填空题(每题4分,共24分)
-
11. 如图,将先沿折叠,再沿折叠后,A点落在线段上的处,C点落在E处,连接 , . 若恰有 , 则 .
 12. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .
12. 如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 .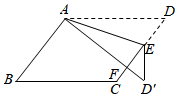 13. 数学活动课上,陈老师向同学们展示了一位同学的折纸作品(如图所示).已知平行四边形纸片 , 对角线 , 点E,F分别在边和上,交于点P.将纸片沿折叠,点A落在外的点处,B落在对角线上的点G处,交于点H,连接 . 若 , 则 .
13. 数学活动课上,陈老师向同学们展示了一位同学的折纸作品(如图所示).已知平行四边形纸片 , 对角线 , 点E,F分别在边和上,交于点P.将纸片沿折叠,点A落在外的点处,B落在对角线上的点G处,交于点H,连接 . 若 , 则 .
三、解答题(共8题,共66分)
-
14. 如图,在平行四边形ABCD中,AB= , BC=8,∠B=60°,将平行四边形ABCD沿EF折叠,点D恰好落在边AB的中点D'处,折叠后点C的对应点为点C' ,D'C'交BC于点G,∠BGD'=32°.求:
 (1)、∠D'EF的度数;(2)、线段AE的长.15. 如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的D'处,折痕交CD边于点E,连结BE.
(1)、∠D'EF的度数;(2)、线段AE的长.15. 如图,将ABCD沿过点A的直线l折叠,使点D落到AB边上的D'处,折痕交CD边于点E,连结BE. (1)、求证:四边形BCED'是平行四边形;(2)、若BE平分∠ABC,求证:AB2=AE2+BE2 .16. 如图,在中,点E是边上一点,将沿折叠后,点B的对应点为点F.
(1)、求证:四边形BCED'是平行四边形;(2)、若BE平分∠ABC,求证:AB2=AE2+BE2 .16. 如图,在中,点E是边上一点,将沿折叠后,点B的对应点为点F. (1)、如图1,连接 , 若点F恰好落在边上.
(1)、如图1,连接 , 若点F恰好落在边上.①求证:;
②求的长;
(2)、如图2,连接 , 若 , 求的长.17. 如图,在平面直角坐标系中,的顶点O,B的坐标分别为 , , 将沿对角线翻折得到(点O,A,D在同一直线上),边与边相交于点E,此时,是等边三角形.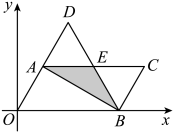 (1)、求线段的长;(2)、求重叠部分的面积;(3)、点N在轴上,点M在直线上,若以点B,C,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.18. 如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB.
(1)、求线段的长;(2)、求重叠部分的面积;(3)、点N在轴上,点M在直线上,若以点B,C,M,N为顶点的四边形是平行四边形时,请直接写出点M的坐标.18. 如图,在平行四边形ABCD中,AB=10,AD=16,∠A=60°,P是射线AD上一点,连接PB,沿PB将△APB折叠,得△A'PB. (1)、如图1所示,当∠DPA'=10°时,∠A'PB=度;(2)、如图2所示,当PA'⊥BC时,求线段PA的长度;(3)、当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.19. 如图,在四边形中, .
(1)、如图1所示,当∠DPA'=10°时,∠A'PB=度;(2)、如图2所示,当PA'⊥BC时,求线段PA的长度;(3)、当点P为AD中点时,点F是边AB上不与点A,B重合的一个动点,将△APF沿PF折叠,得到△A'PF,连接BA',求△BA'F周长的最小值.19. 如图,在四边形中, .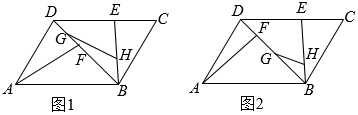 (1)、如图1,求证:四边形是平行四边形;(2)、如图1,连接 , 射线沿翻折交边于点E,点F,G在上,点H在上,连接 , 若 , 求证:;(3)、如图2,在(2)的条件下,G为中点,若 , , 求的长.20.(1)、问题提出
(1)、如图1,求证:四边形是平行四边形;(2)、如图1,连接 , 射线沿翻折交边于点E,点F,G在上,点H在上,连接 , 若 , 求证:;(3)、如图2,在(2)的条件下,G为中点,若 , , 求的长.20.(1)、问题提出在平面内,已知线段 , , 则线段的最小值为 .
(2)、问题探究如图1,在平行四边形中, , , , P是边的中点,Q是边上一动点,将三角形沿所在直线翻折,得到三角形 , 连接 , 求的最小值.
(3)、问题解决如图2,平行四边形为某公园平面示意图,扇形为该公园的人口广场,已知 , , , . 为了提升游客体验感,工作人员准备在弧上找一点P , 沿 , 修两条绿色通道,并在上方和右方区域种植花卉供游客观赏,其余地方修建其他设施,求其他设施区域面积的最小值.
 21. 我们知道平行四边形有很多性质.现在如果我们把平行四边形沿着它的一条对角线翻折.会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,AB=2 , ∠30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
21. 我们知道平行四边形有很多性质.现在如果我们把平行四边形沿着它的一条对角线翻折.会发现这其中还有更多的结论,如图,已知平行四边形ABCD中,AB=2 , ∠30°,AB≠BC,将△ABC沿AC翻折至△AB′C,连接B′D.
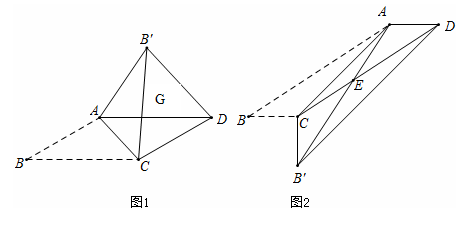 (1)、【发现与证明】
(1)、【发现与证明】如图1:结论①△AGC是等腰三角形;结论②B′D∥AC。请证明结论①或结论②(只需证明一个结论)。
(2)、【应用与解答】如图2:如果BC=1,AB′与CD相交于点E,求△AEC的面积。
(3)、【拓展与探索】直接写出结论,当BC的长为多少时,△AB′D是直角三角形?