2024年北师大版数学八(下)微素养核心突破9 平行四边形的动点问题
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题(每题3分,共27分)
-
1. 如图,等腰中, , 点是底边上的一动点(不与点重合),过点分别作的平行线 , 交于点 , 则下列数量关系一定正确的是( )
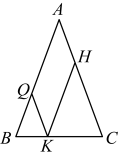 A、 B、 C、 D、2. 如图,直线 , 它们间的距离为2,在直线下方有一定点 , 到的距离为1,点分别是上的动点,平面内一点与三点构成 , 则对角线长度的最小值是( )
A、 B、 C、 D、2. 如图,直线 , 它们间的距离为2,在直线下方有一定点 , 到的距离为1,点分别是上的动点,平面内一点与三点构成 , 则对角线长度的最小值是( ) A、3 B、4 C、5 D、63. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )
A、3 B、4 C、5 D、63. 如图,在平行四边形中, , , , , 分别是边 , 上的动点,连接 , , , 分别是 , 的中点,连接 , 则的最大值与最小值的差为( )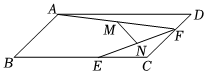 A、 B、 C、 D、4. 如图,在给定的△ABC中,动点D从点B出发沿BC方向向终点C运动,DEAC交AB于点E,DFAB交AC于点F,O是EF的中点,在整个运动过程中,△OBC的面积的大小变化情况是( )
A、 B、 C、 D、4. 如图,在给定的△ABC中,动点D从点B出发沿BC方向向终点C运动,DEAC交AB于点E,DFAB交AC于点F,O是EF的中点,在整个运动过程中,△OBC的面积的大小变化情况是( ) A、不变 B、一直增大 C、先增大后减小 D、先减小后增大5. 如图,在平面直角坐标系中, , 两点坐标分别为 , , 为线段上的一动点,以 , 为边构造平行四边形 , 则使对角线值最小的点的坐标为( )
A、不变 B、一直增大 C、先增大后减小 D、先减小后增大5. 如图,在平面直角坐标系中, , 两点坐标分别为 , , 为线段上的一动点,以 , 为边构造平行四边形 , 则使对角线值最小的点的坐标为( ) A、 B、 C、 D、6. 如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( )
A、 B、 C、 D、6. 如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF.则EF的最大值与最小值的差为( ) A、1 B、1 C、 D、27. 如图,△ABC中,∠BAC=45°,AB=AC=8,P为AB边上的一动点,以PA,PC为边作平行四边形PAQC,则线段AQ长度的最小值为( )
A、1 B、1 C、 D、27. 如图,△ABC中,∠BAC=45°,AB=AC=8,P为AB边上的一动点,以PA,PC为边作平行四边形PAQC,则线段AQ长度的最小值为( ) A、6 B、8 C、 D、8. 如图,等边的边长为 , 射线 , 点E从点A出发沿射线以的速度运动,点F从点B出发沿射线以的速度运动.设运动时间为 , 当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形.
A、6 B、8 C、 D、8. 如图,等边的边长为 , 射线 , 点E从点A出发沿射线以的速度运动,点F从点B出发沿射线以的速度运动.设运动时间为 , 当t=( )s时,以A、C、E、F为顶点的四边形是平行四边形. A、1或2 B、2或3 C、2或4 D、2或69. 如图,四边形中, , . 点从点A出发,以的速度向点D运动;点从点C同时出发,以的速度向点B运动.规定其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为秒,下列结论错误的是( )
A、1或2 B、2或3 C、2或4 D、2或69. 如图,四边形中, , . 点从点A出发,以的速度向点D运动;点从点C同时出发,以的速度向点B运动.规定其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为秒,下列结论错误的是( ) A、当时, B、当时, C、当或时, D、当时,四边形的最大面积为
A、当时, B、当时, C、当或时, D、当时,四边形的最大面积为二、填空题(每题3分,共18分)
-
10. 如图,四边形ABCD 是平行四边形,点D 的纵坐标是6,CD=10,顶点A在y轴上,边 BC 在x轴上.设 P 是射线 BC上的一个动点,则当△ABP 为等腰三角形时,点P的坐标是.
 11. 如图,在▱ABCD中,AD=3cm,动点P以每秒0.5cm的速度从点A向点D运动,另一动点Q以每秒1cm的速度从点C出发,在BC间往返运动,P、Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若P,D,Q,B四点组成的四边形是平行四边形时,则运动时间为秒.
11. 如图,在▱ABCD中,AD=3cm,动点P以每秒0.5cm的速度从点A向点D运动,另一动点Q以每秒1cm的速度从点C出发,在BC间往返运动,P、Q两点同时出发,当点P到达点D时停止运动(同时Q点也停止),若P,D,Q,B四点组成的四边形是平行四边形时,则运动时间为秒. 12. 如图,中, , 若D , E是边上的两个动点,F是边上的一个动点, , 则的最小值为 .
12. 如图,中, , 若D , E是边上的两个动点,F是边上的一个动点, , 则的最小值为 . 13. 如图,在▱中,对角线 , 交于点 , , , 过点作的平分线的垂线,垂足为点 , 若点在的垂直平分线上,是直线上的动点,则的最小值为 .
13. 如图,在▱中,对角线 , 交于点 , , , 过点作的平分线的垂线,垂足为点 , 若点在的垂直平分线上,是直线上的动点,则的最小值为 . 14. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 .
14. 如图,▱ABCD中∠D=75°,AB=4,AC=BC,点E为线段AD上一动点,过点E作EF⊥AC于点F,连接BE,点G为BE中点,连接GF.当GF最小时,线段AF的值为 . 15. 如图,▱中 , , , 为边上一点,则的最小值为 .
15. 如图,▱中 , , , 为边上一点,则的最小值为 .
三、解答题(共9题,共75分)
-
16. 如图,在平行四边形ABCD中,AB=6cm,AD=10cm,点P在AD边上以每秒1cm的速度从点A向点D运动点Q在CB边上以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止运动,同时点Q也停止运动.设运动时间为ts,当t为何值时,以P,D,Q,B为顶点的四边形是平行四边形?
 17. 如图,点B是的边上的定点,点C是边上的动点,将绕点B逆时针旋转得到 , 且点A的对应点D恰好落在边上,连接 . 点F是上一点,连接 , 且点F到的距离等于点F到的距离.当时.
17. 如图,点B是的边上的定点,点C是边上的动点,将绕点B逆时针旋转得到 , 且点A的对应点D恰好落在边上,连接 . 点F是上一点,连接 , 且点F到的距离等于点F到的距离.当时. (1)、求证:四边形是平行四边形;(2)、若 , 求的度数.18. 如图,AM是的中线,是线段AM上一点(不与点A重合),DE//AB,交AC于点 , 交DF于点 , 连结AE.
(1)、求证:四边形是平行四边形;(2)、若 , 求的度数.18. 如图,AM是的中线,是线段AM上一点(不与点A重合),DE//AB,交AC于点 , 交DF于点 , 连结AE. (1)、如图①,当点D与点M重合时,求证:四边形ABDE是平行四边形.(2)、如图②,当点D不与点M重合时,(1)中的结论还成立吗?请说明理由.19. 如图,在四边形 ABCD中,AD∥BC,AD=12cm,BC=15cm,点P从点A 出发向点D 以1cm/s的速度运动,到点 D 即停止.点Q从点C 出发向点 B以2cm/s的速度运动,到点B即停止,点P,Q同时出发,设运动时间为t(s)..
(1)、如图①,当点D与点M重合时,求证:四边形ABDE是平行四边形.(2)、如图②,当点D不与点M重合时,(1)中的结论还成立吗?请说明理由.19. 如图,在四边形 ABCD中,AD∥BC,AD=12cm,BC=15cm,点P从点A 出发向点D 以1cm/s的速度运动,到点 D 即停止.点Q从点C 出发向点 B以2cm/s的速度运动,到点B即停止,点P,Q同时出发,设运动时间为t(s).. (1)、用含 t的代数式表示:
(1)、用含 t的代数式表示:AP=cm,DP=cm,
BQ=cm,CQ=cm
(2)、当t为何值时,四边形APQB 是平行四边形?(3)、当t为何值时,四边形PDCQ是平行四边形?20. 如图,M,N是▱ABCD对角线BD上两点. (1)、若 BM=MN=DN,求证:四边形 AMCN 为平行四边形.(2)、若 M,N 为对角线 BD 上的动点(均可与端点重合),设 BD=12cm,点M由点B 向点D 匀速运动,速度为 2cm/s,同时点N由点D 向点B匀速运动,速度为 a(cm/s),运动时间为 t(s).若要使四边形AMCN为平行四边形,求a的值及t的.取值范围.21. 如图1,中, , D为上一动点,E为延长线上的动点,始终保持 , 连接和 , 以为边作正方形 , 连接 .
(1)、若 BM=MN=DN,求证:四边形 AMCN 为平行四边形.(2)、若 M,N 为对角线 BD 上的动点(均可与端点重合),设 BD=12cm,点M由点B 向点D 匀速运动,速度为 2cm/s,同时点N由点D 向点B匀速运动,速度为 a(cm/s),运动时间为 t(s).若要使四边形AMCN为平行四边形,求a的值及t的.取值范围.21. 如图1,中, , D为上一动点,E为延长线上的动点,始终保持 , 连接和 , 以为边作正方形 , 连接 .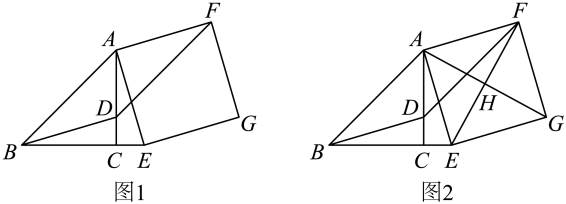 (1)、请判断四边形的形状,并说明理由;(2)、当时,求的度数;22. 如图①,在平行四边形ABCD中, AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D .设点P运动的时间为t(t>0)秒.
(1)、请判断四边形的形状,并说明理由;(2)、当时,求的度数;22. 如图①,在平行四边形ABCD中, AB=3,AD=6.动点P沿AD边以每秒个单位长度的速度从点A向终点D .设点P运动的时间为t(t>0)秒.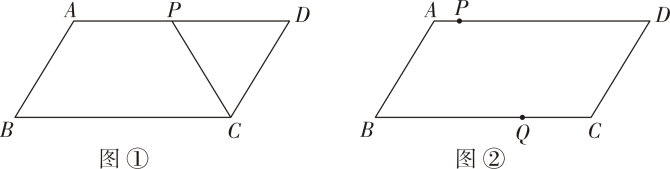 (1)、线段PD的长为 (用含t的代数式表示).(2)、当CP平分∠BCD时,求t的值.(3)、如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,点Q也随之停止运动.当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.23. 如图,在中, , , . 动点从点出发沿以速度向终点运动,同时点从点出发,以速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒 .
(1)、线段PD的长为 (用含t的代数式表示).(2)、当CP平分∠BCD时,求t的值.(3)、如图②,另一动点Q以每秒2个单位长度的速度从点C出发,在CB上往返运动.P、Q两点同时出发,点Q也随之停止运动.当以P、D、Q、B为顶点的四边形是平行四边形时,直接写出t的值.23. 如图,在中, , , . 动点从点出发沿以速度向终点运动,同时点从点出发,以速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒 .


(备用图) (备用图)
(1)、的长为cm.(2)、当时,用含的代数式表示线段的长 .(3)、连结 . 是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由.(4)、若点关于直线对称的点恰好落在直线上,请直接写出的值.24. 如图1,在平面直角坐标系中,直线:与坐标轴交于 , 两点,点为的中点,动点从点出发,沿方向以每秒1个单位的速度向终点运动,同时动点从点出发,以每秒2个单位的速度沿射线方向运动,当点到达点时,点也停止运动以 , 为邻边构造▱ , 设点运动的时间为秒. (1)、直接写出点的坐标为 .(2)、如图2,过点作轴于 , 过点作轴于证明:≌ .(3)、如图3,连结 , 当点恰好落在的边所在的直线上时,求所有满足要求的的值.
(1)、直接写出点的坐标为 .(2)、如图2,过点作轴于 , 过点作轴于证明:≌ .(3)、如图3,连结 , 当点恰好落在的边所在的直线上时,求所有满足要求的的值.