2024年北师大版数学八（下）微素养核心突破8 分式与分式方程

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列式子： $- 5 x$ ， $\frac{1}{a + b}$ ， $\frac{1}{2} a^{2} - \frac{1}{2} b^{2}$ ， $\frac{3}{10 m}$ ， $\frac{2}{π}$ ，其中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若分式 $\frac{x + 2}{x^{2} - 4}$ 有意义，则x的取值范围是（）

A、 $x \neq 0$ B、 $x \neq - 2$ C、 $x \neq 2$ D、 $x \neq \pm 2$

查看试题解析
3. 若 $x$ 、 $y$ 的值均扩大为原来的 $5$ 倍，则下列分式的值保持不变的是（）

A、 $\frac{x + y}{x y}$ B、 $\frac{x + y}{x - y}$ C、 $\frac{x + y}{y + 1}$ D、 $\frac{x}{y + 1}$

查看试题解析
4. 下列分式中，最简分式是（）

A、 $\frac{4 x}{x^{2}}$ B、 $\frac{x + 1}{x - 1}$ C、 $\frac{6}{9 x}$ D、 $\frac{x - 1}{x^{2} - 1}$

查看试题解析
5. 下列运算中正确的是（）

A、 $\frac{0.2 a + b}{0.7 a - b}$ ＝ $\frac{2 a + b}{7 a - b}$ B、 $\frac{a - b}{b - a} = - 1$ C、 $\frac{- b}{2 a^{2}}$ • $\frac{a}{- b^{2}}$ ＝﹣ $\frac{1}{2 a b}$ D、 $\frac{m}{x} \div \frac{n}{x} = \frac{n}{m}$

查看试题解析
6. 已知x≠0，则 $\frac{1}{x} + \frac{1}{2 x} + \frac{1}{3 x}$ 等于（）

A、 $\frac{1}{2 x}$ B、 $\frac{1}{6 x}$ C、 $\frac{5}{6 x}$ D、 $\frac{11}{6 x}$

查看试题解析
7. 计算 $\frac{x}{x^{2} - y^{2}} - \frac{y}{x^{2} - y^{2}}$ 的结果是（）

A、 $\frac{1}{x - y}$ B、 $\frac{1}{x + y}$ C、 $x - y$ D、1

查看试题解析
8. 已知关于x不等式组 ${\begin{array}{l} 2 x - 3 a < 2 \\ x - 2 b > 3 \end{array}$ 的解集为 $- 1 < x < 2$ ，则代数式 $(a - \frac{b^{2}}{a}) \cdot \frac{a}{a - b}$ 的值是（）

A、 $\frac{2}{3}$ B、-2 C、 $- \frac{8}{3}$ D、 $- \frac{4}{3}$

查看试题解析
9. 几个同学包租一辆面包车去旅游，面包车的租价为180元，后来又增加了两名同学，租车价不变，结果每个同学比原来少分摊了3元车费．若设原计划参加旅游的同学共有 $x$ 人，则根据题可列方程（　　）

A、 $\frac{180}{x} - \frac{180}{x + 2} = 3$ B、 $\frac{180}{x + 2} - \frac{180}{x} = 3$ C、 $\frac{180}{x} - \frac{180}{x + 3} = 2$ D、 $\frac{180}{x + 3} - \frac{180}{x} = 2$

查看试题解析
10. 关于x的分式方程 $\frac{x}{x + 2} - \frac{x + 2}{x - 2} = \frac{m}{x^{2} - 4}$ 的解为正数，则m的取值范围是（　　）

A、m＜﹣4 B、m＞﹣4 C、m＜﹣4且m≠﹣16 D、m＞﹣4且m≠8

查看试题解析

二、填空题（每题4分，共24分）

11. 若分式 $\frac{| x | - 3}{x - 3}$ 的值为零，则 $x$ =。

查看试题解析
12. 已知n为整数，当 $n =$ 时，分式 $\frac{2}{n - 1}$ 的值是整数．

查看试题解析
13. 化简 $\frac{2 x + 2 y}{5 a^{2} b} \cdot \frac{10 a b^{2}}{x^{2} - y^{2}}$ 的结果为。

查看试题解析
14. 分式： $\frac{1}{4 a}$ ， $\frac{2}{3 b^{2}}$ ， $\frac{1}{2 a b}$ 的最简公分母是．

查看试题解析
15. 若关于 $x$ 的分式方程 $\frac{x}{x - 2} + \frac{m + 1}{2 - x} = 3$ 有非负整数解，且关于 $y$ 的不等式组 ${\begin{array}{l} \frac{y}{2} + 1 \geq \frac{y + 2}{3} \\ 5 (y - 1) (y - (m + 3) \end{array}$ 有且只有2个整数解，则所有符合条件的 $m$ 的和是．

查看试题解析
16. 用换元法解方程 $\frac{3 x}{x^{2} - 1} - \frac{x^{2} - 1}{x} = 2$ ，如果设 $y = \frac{x}{x^{2} - 1}$ ，那么原方程可以化为关于y的整式方程为．

查看试题解析

三、计算题（共3题，共17分）

17. 先化简，再求值： $\frac{a^{2} + 2 a b + b^{2}}{a + b} \div (\frac{1}{b} + \frac{1}{a})$ ，其中 $a = \sqrt{2} + 1 ， b = \sqrt{2} - 1$ ．

查看试题解析
18. 解方程

(1)、 $\frac{2}{x + 5} = \frac{1}{2 x - 1}$

(2)、 $\frac{5 x - 4}{x - 2} - \frac{4 x + 10}{3 x - 6} = - 1$

查看试题解析
19. 先化简，再求值： $\frac{4}{x^{2} + x} \div (1 - \frac{x - 1}{x^{2} - 1})$ ，其中 $x$ 是不等式组 ${\begin{array}{l} 3 - 5 x \leq 8 \\ 2 (x - 1) < x + 1 \end{array}$ 的整数解．

查看试题解析

四、解答题（共5题，共49分）

20.

(1)、计算： ${(π - 3)}^{0} - (\frac{1}{3})^{- 2} + {(- 1)}^{2022}$

(2)、下面是小彬同学进行分式化简的过程，请认真阅读并完成相应任务．
$\frac{x^{2} - 9}{x^{2} + 6 x + 9}$ - $\frac{2 x + 1}{2 x + 6}$ ＝ $\frac{(x + 3) (x - 3)}{(x + 3)^{2}}$ - $\frac{2 x + 1}{2 (x + 3)}$ …第一步

＝ $\frac{x - 3}{x + 3}$ - $\frac{2 x + 1}{2 (x + 3)}$ …第二步

＝ $\frac{2 (x - 3)}{2 (x + 3)}$ - $\frac{2 x + 1}{2 (x + 3)}$ …第三步

＝ $\frac{2 x - 6 - (2 x + 1)}{2 (x + 3)}$                …第四步

$\frac{2 x - 6 - 2 x + 1}{2 (x + 3)}$                  …第五步

＝- $\frac{5}{2 x + 6}$ …第六步
任务一：填空：
①以上化简步骤中，第步是进行分式的通分，通分的依据是；

② 第步开始出现错误，这一步错误的原因是．

(3)、任务二：请直接写出该分式化简后的正确结果；

(4)、任务三：除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议．

查看试题解析
21. 某水果店用1350元购进一批车厘子，受到消费者的欢迎，于是又用了2450元购进第二批，由于第二批的采购量是第一批的2倍，所以比第一批车厘子每斤的进价便宜了5元．

(1)、求第一批和第二批车厘子的进价分别为每斤多少元；

(2)、在销售过程中，水果店以每斤80元的价格销售完了第一批车厘子和第二批车厘子的 $\frac{3}{5}$ ，为了回流资金，决定降价销售余下的车厘子，若两批车厘子的总利润不低于1800元，求降价后的车厘子售价每斤至少多少元；

查看试题解析
22. 已知甲、乙两地相距 $360$ 千米，一辆货车和一辆轿车先后从甲地出发前往乙地，轿车比货车晚出发2小时，轿车每小时比货车多行驶30千米，最后同时到达．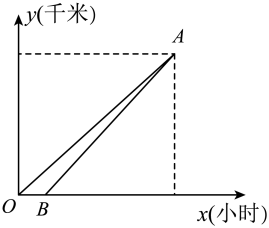

(1)、求货车的速度；

(2)、设货车行驶时间为x小时，离甲地的距离是y千米，如图，线段 $O A 、 B A$ 分别表示货车、轿车离甲地距离y（千米）与x（小时）之间的函数关系，那么点A的坐标是；线段 $B A$ 对应的函数解析式为．（不需要写出定义域）

查看试题解析
23. “文房四宝”是中国独有的书法绘画工具，即笔、墨、纸、砚，文房四宝之名起源于南北朝时期，为丰富学生的课后服务活动，重庆第八中学准备为社团购买 $A$ ， $B$ 两种型号“文房四宝”，通过市场调研得知： $A$ 种型号“文房四宝”的单价比 $B$ 种“文房四宝”的单价多100元，且用22500元购买 $A$ 种型号“文房四宝”的数量是用10000元购买 $B$ 种“文房四宝”数量的1.5倍．

(1)、求 $A$ ， $B$ 两种型号“文房四宝”的单价分别是多少元？

(2)、该学校计划用不超过10000元的资金购买 $A$ ， $B$ 两种型号“文房四宝”共40组，为使购买的 $A$ 种型号“文房四宝”的数量尽可能多，请设计出购买方案．

查看试题解析
24. 阅读下列材料：通过小学的学习我们知道，分数可分为“真分数”和“假分数”，而假分数都可以化为带分数，如： $\frac{8}{3} = \frac{6 + 2}{3} = 2 + \frac{2}{3} = 2 \frac{2}{3}$ ．我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”． $\frac{x - 1}{x + 1} ， \frac{x^{2}}{x - 1}$ ，这样的分式就是假分式；再如： $\frac{3}{x + 1} ， \frac{2 x}{x^{2} + 1}$ 这样的分式就是真分式．类似的，假分式也可以化为带分式（即：整式与真分式的和的形式），如： $\frac{x - 1}{x + 1} = \frac{(x + 1) - 2}{x + 1} = 1 - \frac{2}{x + 1}$ ；
解决下列问题：

(1)、分式 $\frac{1}{3 x^{2}}$ 是（填“真分式”或“假分式”）；

(2)、将假分式 $\frac{4 a + 1}{2 a - 1}$ 化为整式与真分式的和的形式： $\frac{4 a + 1}{2 a - 1}$ =；

(3)、若假分式 $\frac{4 a + 1}{2 a - 1}$ 的值为正整数，则整数 $a$ 的值为；

(4)、将假分式 $\frac{x^{2} - 2 x - 1}{x - 1}$ 化为带分式（写出完整过程）．

查看试题解析