贵州省2023-2024学年七年级下学期数学期末考试仿真试卷(五)
试卷更新日期:2024-06-02 类型:期末考试
一、选择题
-
1. 有理数的相反数是( )A、 B、 C、2024 D、2. 下列说法不正确的是( )A、为了审核书稿中的错别字,选择普查
B、为了解春节联欢晚会的收视率,选择抽样调查
C、为了清楚地反映事物的变化情况,可选用扇形统计图
D、频数与总次数的比值是频率3. 下列各组数是方程解的是( )A、 B、 C、 D、4. 如图,在线段 、 、 、 中,长度最小的是( ) A、线段 B、线段 C、线段 D、线段5. 已知轴,且点的坐标为 , 点的坐标为 , 则点的纵坐标为( )A、3 B、4 C、0 D、-36. 已知实数a,b,若 , 则下列结论正确的是( )A、 B、 C、 D、7. 在解方程组的过程中,将②代入①可得( )A、 B、 C、 D、8. 满足的整数x有( )A、1个 B、2个 C、3个 D、4个9. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )
A、线段 B、线段 C、线段 D、线段5. 已知轴,且点的坐标为 , 点的坐标为 , 则点的纵坐标为( )A、3 B、4 C、0 D、-36. 已知实数a,b,若 , 则下列结论正确的是( )A、 B、 C、 D、7. 在解方程组的过程中,将②代入①可得( )A、 B、 C、 D、8. 满足的整数x有( )A、1个 B、2个 C、3个 D、4个9. 一次数学活动中,小明对纸带沿AB折叠,量得 , 则的度数为( )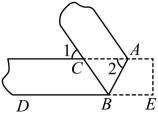 A、 B、 C、 D、10. 《九章算术》中记载了一个问题,原文如下:“今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?”大意是:有几个人一起去买一件物品,每人出8文,多3文;每人出7文,少4文,求人数及该物品的价格,小明用二元一次方程组解决此问题,若已经列出一个方程 , 则符合题意的另一个方程是( )A、 B、 C、 D、11. 如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
A、 B、 C、 D、10. 《九章算术》中记载了一个问题,原文如下:“今有人共买物,人出八,盈三;人出七,不足四.问人数,物价各几何?”大意是:有几个人一起去买一件物品,每人出8文,多3文;每人出7文,少4文,求人数及该物品的价格,小明用二元一次方程组解决此问题,若已经列出一个方程 , 则符合题意的另一个方程是( )A、 B、 C、 D、11. 如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( ) A、57° B、58° C、59° D、60°
A、57° B、58° C、59° D、60°二、填空题
-
12. 在平面直角坐标系中,将点先向右平移1个单位长度、再向下平移2个单位长度得到点B , 则B的坐标是 .13. 化简的结果是。14. 如图,已知 ,点 在 上,点 为平面内一点, ,过点 作 平分 平分 ,若 ,则 .

三、解答题
-
15. 解方程组 , 下面是两同学的解答过程:
小敏:解:把方程变形为 ,
再将代入方程①得….
小川:解:将方程的两边乘以3得 , 再将两个方程相加,得到….
(1)、小敏的解法依据是 , 运用的方法是;小川的解法依据是 , 运用的方法是;
①整式的运算性质;②等式的性质;③加法的结合律;④代入消元法;⑤加减消元法.
(2)、请直接写出原方程组的解.16. 为了进一步了解某校八年级学生的身体素质情况,体育老师抽测了该校八年级(1)班50名学生一分钟的跳绳次数,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:请结合图表完成下列问题:组别
次数
频数(人数)
第1组
6
第2组
8
第3组
第4组
18
第5组
6
 (1)、本次调查为(填全面调查或抽样调查),样本容量为;(2)、 ▲ ;并把频数分布直方图补充完整;(3)、若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?17. 如图,在平面直角坐标系中, , , , 将先向左平移个单位长度,再向上平移个单位长度,得到 .
(1)、本次调查为(填全面调查或抽样调查),样本容量为;(2)、 ▲ ;并把频数分布直方图补充完整;(3)、若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?17. 如图,在平面直角坐标系中, , , , 将先向左平移个单位长度,再向上平移个单位长度,得到 .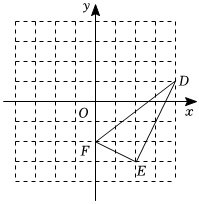 (1)、画出 , 写出、两点的坐标;
(1)、画出 , 写出、两点的坐标;
(2)、求的面积.18.(1)、已知某正数的平方根为a+3和2a-9,求这个数是多少?(2)、已知 , 是实数,且 , 求的平方根.19. 如图,点E , F分别在线段AB , CD上,AB∥CD , ∠BED=∠AFC . (1)、求证:AF∥DE .
(1)、求证:AF∥DE .证明:∵AB∥CD(已知),
∴∠BED=∠D( ▲ ).
∵∠BED=∠AFC(已知),
∴∠D=∠ ▲ (等量代换).
∴ ▲ ( ▲ ).
(2)、若∠A=50°,求∠D的度数.20. 超市购进A、B两种商品,购进4件A种商品比购进5件B种商品少用10元,购进20件A种商品和10件B种商品共用去160元.(1)、求A、B两种商品每件进价分别是多少元?(2)、若该商店购进A、B两种商品共200件,都标价10元出售,售出一部分商品后降价促销,以标价的八折售完所有剩余商品,以10元售出的商品件数比购进A种商品的件数少30件,该商店此次销售A、B两种商品共获利不少于640元,求至少购进A种商品多少件?21.(1)、比较下列各式的大小:(用“<”“>”或“=”连接)|(+3)+(+8)| |+3|+|+8|; |(-3)+(-8)| |-3|+|-8|;
|(-3)+(+8)| |-3|+|+8|; |(+3)+(-8)| |+3|+|-8|;
|0+(+8)| 0+|-8|;
(2)、通过(1)的比较,请你分析,归纳出当 a,b 为有理数时,|a|+|b|与|a+b|的大小关系是|a|+|b||a+b|(填“ < ”“ > ”“ ≤ ”“ ≥ ”或“=”)(3)、根据(2)中你得出的结论,求当|x-2019|=|x|+2019 时,x 的取值范围.22. 解下列方程或不等式 .(1)、;
(2)、 .23. 在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线射到平面镜上,被反射后的光线为 , 则入射光线、反射光线与平面镜所夹的锐角 .
 (1)、【简单应用】
(1)、【简单应用】如图2,有一口井,已知入射光线与水平线的夹角为 , 现放置平面镜 , 可使反射光线正好垂直照射到井底(即射线),与水平线的夹角的度数为 .
(2)、【类比拓展】如图3,有两块平面镜 , 且 , 入射光线经过两次反射,得到反射光线 . 由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即: . 在这样的条件下,求证: .
(3)、【尝试探究】两块平面镜 , 且 , 入射光线经过两次反射,得到反射光线 . 如图4,光线与相交于点 , 则的度数是多少?(用含的式子表示)(三角形内角和)