2024年北师大版数学七(下)重难点培优训练10 角平分线与线段垂直平分线
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 如图,用直尺和圆规作出的角平分线 , 在作角平分线过程中,用到的三角形全等的判定方法是( )
 A、 B、 C、 D、2. 如图,在中, , 边的垂直平分线分别交、于点、 , 连接 , 若平分 , 则图中与全等的三角形有( )
A、 B、 C、 D、2. 如图,在中, , 边的垂直平分线分别交、于点、 , 连接 , 若平分 , 则图中与全等的三角形有( )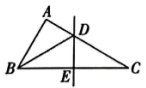 A、0个 B、1个 C、2个 D、3个3. 如图, , ,若 , ,则点D到 的距离为( )
A、0个 B、1个 C、2个 D、3个3. 如图, , ,若 , ,则点D到 的距离为( )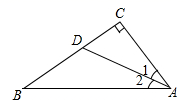 A、4 B、6 C、8 D、104. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是( )
A、4 B、6 C、8 D、104. 如图,射线是的角平分线,是射线上一点,于点 , , 若点是射线上一点, , 则的面积是( ) A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,首先以顶点B为圆心,任意长度为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心,大于为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=4,P为边AB上一动点,则GP的最小值为( )
A、 B、 C、 D、5. 如图,在Rt△ABC中,∠C=90°,首先以顶点B为圆心,任意长度为半径作弧,在边BC、BA上截取BE、BD;然后分别以点D、E为圆心,大于为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=4,P为边AB上一动点,则GP的最小值为( ) A、2 B、8 C、4 D、无法确定6. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )
A、2 B、8 C、4 D、无法确定6. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )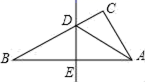 A、10cm B、12cm C、15cm D、17cm7. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , . 若 , 的周长为 , 则的周长为( )
A、10cm B、12cm C、15cm D、17cm7. 如图,在中,分别以 , 为圆心,大于长为半径作弧,两弧分别相交于 , 两点,作直线 , 分别交线段 , 于点 , . 若 , 的周长为 , 则的周长为( )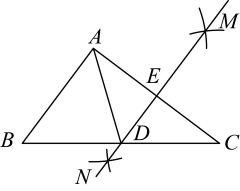 A、 B、 C、 D、8. 已知:如图,在中,的垂直平分线交于点 , 的垂直平分线交于点若 , 则的度数为( )
A、 B、 C、 D、8. 已知:如图,在中,的垂直平分线交于点 , 的垂直平分线交于点若 , 则的度数为( ) A、 B、 C、 D、9. 如图,在中,按以下步骤作图:①分别以点B和点C为圆心,大于的长为半径作弧,两弧相交于点M和N , 连接 , 分别与 , 交于点D和E;②以点A为圆心,任意长为半径作弧,交于点G , 交于点H;③分别以点G和点H为圆心,大于的长为半径作弧,两弧相交于点P;④作射线 , 分别交 , 于点F , Q . 若 , , 则的度数为( )
A、 B、 C、 D、9. 如图,在中,按以下步骤作图:①分别以点B和点C为圆心,大于的长为半径作弧,两弧相交于点M和N , 连接 , 分别与 , 交于点D和E;②以点A为圆心,任意长为半径作弧,交于点G , 交于点H;③分别以点G和点H为圆心,大于的长为半径作弧,两弧相交于点P;④作射线 , 分别交 , 于点F , Q . 若 , , 则的度数为( ) A、 B、 C、 D、10. 如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )
A、 B、 C、 D、10. 如图,在 中, ,点D是BC边的中点,连接AD,点P在AD上,连接BP,CP,过点D作 , ,垂足分别为E、F,则下列结论:① ;② ;③ ;④ 是等腰三角形.其中正确的有( )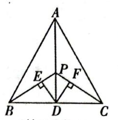 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题4分,共24分)
-
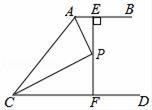
11. 如图,AB∥CD,∠BAC与∠ACD的平分线交于点P,过P作PE⊥AB于E,交CD于F,EF=10,则点P到AC的距离为 .
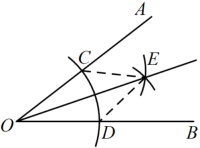
 12. 如图,BO平分于点D,点E为射线BA上一动点,若 , 则OE的最小值为.
12. 如图,BO平分于点D,点E为射线BA上一动点,若 , 则OE的最小值为.
 13. 如图,以的顶点O为圆心,以任意长为半径作弧分别交 , 于M,N两点:分别以点M,N为圆心,以大于的长为半径作弧,两弧相交于点P;作射线 , 若点Q在射线上且到边的距离恰好为 , 则点Q到边的距离为 .
13. 如图,以的顶点O为圆心,以任意长为半径作弧分别交 , 于M,N两点:分别以点M,N为圆心,以大于的长为半径作弧,两弧相交于点P;作射线 , 若点Q在射线上且到边的距离恰好为 , 则点Q到边的距离为 . 14. 如图,在△ABC中,AB=AC=10cm,BC=8cm,AB的垂直平分线交AB于点M,交AC于点N,在直线MN上存在一点P,使P、B、C三点构成的△PBC的周长最小,则△PBC的周长最小值为 .
14. 如图,在△ABC中,AB=AC=10cm,BC=8cm,AB的垂直平分线交AB于点M,交AC于点N,在直线MN上存在一点P,使P、B、C三点构成的△PBC的周长最小,则△PBC的周长最小值为 . 15. 如图,中, , 点是上一点,、的垂直平分线分别交、于点、 , 则的度数为 .
15. 如图,中, , 点是上一点,、的垂直平分线分别交、于点、 , 则的度数为 .
 16. 如图,在△ABC中, , 按以下步骤作图:①分别以B , C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线交于D , 连接 . 若 , 则 .
16. 如图,在△ABC中, , 按以下步骤作图:①分别以B , C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线交于D , 连接 . 若 , 则 .
三、作图题(共2题,共12分)
-
17. 用直尺、圆规作图,不写作法,但要保留作图痕迹.
如图,某小区绿化带内部有两个喷水臂、 , 现欲在内部建一个水泵 , 使得水泵到 , 的距离相等,且到两个喷水管、的距离也相等,请你在图中标出水泵的位置.
 18. 如图,两条公路和相交于点,在的内部有工厂和 , 现要在内部修建一个货站 , 使货站到两条公路、的距离相等,且到两工厂、的距离相等,用尺规作出货站的位置.要求:不写作法,保留作图痕迹,写出结论
18. 如图,两条公路和相交于点,在的内部有工厂和 , 现要在内部修建一个货站 , 使货站到两条公路、的距离相等,且到两工厂、的距离相等,用尺规作出货站的位置.要求:不写作法,保留作图痕迹,写出结论
四、解答题(共6题,共54分)
-
19. 如图,四边形中, , 是的中点,平分 .
 (1)、求证:平分;(2)、若 , , 求 的面积.20. 如图,在中,边的垂直平分线交于点D,边的垂直平分线交于点E,与相交于点O,连接 .
(1)、求证:平分;(2)、若 , , 求 的面积.20. 如图,在中,边的垂直平分线交于点D,边的垂直平分线交于点E,与相交于点O,连接 . (1)、若的周长为8cm,的周长为20cm.
(1)、若的周长为8cm,的周长为20cm.①求线段的长;
②求线段的长.
(2)、若 , 求的度数.21. 如图,在中, , 于点D,平分交于点 , 交于点 , 过点作 , 交于点 , 连接 . (1)、求证:;(2)、求证:;(3)、若 , , 求四边形的面积.22. 如图,在等腰△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG,分别交AD、AC于点E、G,EF⊥AB,垂足为F.
(1)、求证:;(2)、求证:;(3)、若 , , 求四边形的面积.22. 如图,在等腰△ABC中,AB=AC,AD是BC边上的中线,∠ABC的平分线BG,分别交AD、AC于点E、G,EF⊥AB,垂足为F. (1)、试说明:EF=ED;(2)、若∠BAD=25°,求∠C的度数.23. 如图,在中, , 点D为BC边上一点,E为AC延长线上的一点, , F为CB边上一点,连接EF,延长AD交EF于点K, , 过点D作直线于G,延长GD交EF于点H,作平分交AD于点M,过点M作交EF于点N,交GD于点O,交BC于点Q, , 连接GN.
(1)、试说明:EF=ED;(2)、若∠BAD=25°,求∠C的度数.23. 如图,在中, , 点D为BC边上一点,E为AC延长线上的一点, , F为CB边上一点,连接EF,延长AD交EF于点K, , 过点D作直线于G,延长GD交EF于点H,作平分交AD于点M,过点M作交EF于点N,交GD于点O,交BC于点Q, , 连接GN.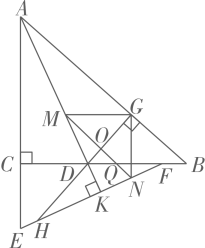 (1)、与相等吗?为什么?(2)、试说明 .24. 教材呈现:如图是北师大版七年级下册数学教材第123页的部分内容,
(1)、与相等吗?为什么?(2)、试说明 .24. 教材呈现:如图是北师大版七年级下册数学教材第123页的部分内容, (1)、请根据所给教材内容,写出结论:(填“”、“”或“”)(2)、结合教材上的图5—11,证明你的结论.(推理过程请注明理由)(3)、应用上述结论解决下列题目:
(1)、请根据所给教材内容,写出结论:(填“”、“”或“”)(2)、结合教材上的图5—11,证明你的结论.(推理过程请注明理由)(3)、应用上述结论解决下列题目:已知:如图,中,是的垂直平分线,于点D,且D为的中点.

①求证:;(推理过程请注明理由)
②若 , 求的度数.