2024年北师大版数学七(下)重难点培优训练9 翻折问题
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题(每题2分,共20分)
-
1. 如图,已知长方形纸片ABCD,点E,F在AD边上,点G,H在BC边上,分别沿EG,FH折叠,使点D和点A都落在点M处,若α+β=119°,则∠EMF的度数为( )
 A、57° B、58° C、59° D、60°2. 如图,将折叠,使点落在边处,展开后得到折痕 , 则是的( )
A、57° B、58° C、59° D、60°2. 如图,将折叠,使点落在边处,展开后得到折痕 , 则是的( ) A、高线 B、角平分线 C、中线 D、中位线3. 如图,将沿直线折叠,使点A落在边上的点F处, , 若 , 则( )
A、高线 B、角平分线 C、中线 D、中位线3. 如图,将沿直线折叠,使点A落在边上的点F处, , 若 , 则( )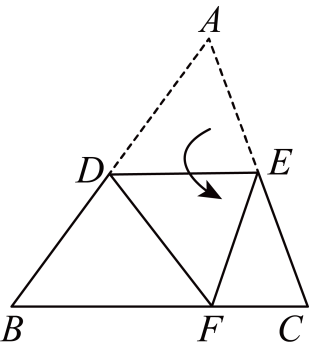 A、 B、 C、 D、4. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 , , 若CD∥BE , , 则的度数是( )
A、 B、 C、 D、4. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为 , , 若CD∥BE , , 则的度数是( ) A、 B、 C、 D、5. 下列四种沿进行折叠的方法中,不一定能判断纸带两条边 , 互相平行的是( )
A、 B、 C、 D、5. 下列四种沿进行折叠的方法中,不一定能判断纸带两条边 , 互相平行的是( ) A、如图1,展开后测得 B、如图2,展开后测得且 C、如图3,展开后测得 D、如图4,展开后测得6. 如图,点E、F分别为长方形纸片ABCD的边AB , CD上的点,将长方形纸片沿EF翻折,点C , B分别落在点C , B处.若∠DFC=a , 则∠FEA-∠AEB的度数为( )
A、如图1,展开后测得 B、如图2,展开后测得且 C、如图3,展开后测得 D、如图4,展开后测得6. 如图,点E、F分别为长方形纸片ABCD的边AB , CD上的点,将长方形纸片沿EF翻折,点C , B分别落在点C , B处.若∠DFC=a , 则∠FEA-∠AEB的度数为( ) A、 B、 C、 D、7. 如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )
A、 B、 C、 D、7. 如图1是长方形纸带,∠DEF=10°,将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中∠CFE度数是多少( )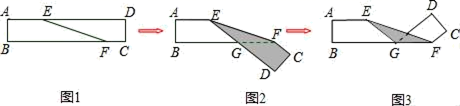 A、160° B、150° C、120° D、110°8. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )
A、160° B、150° C、120° D、110°8. 折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支,折纸过程中既要动脑又要动手.如图,将一长方形纸条首先沿着 进行第一次折叠,使得 , 两点落在 、 的位置,再将纸条沿着 折叠( 与 在同一直线上),使得 、 分别落在 、 的位置.若 ,则 的度数为( )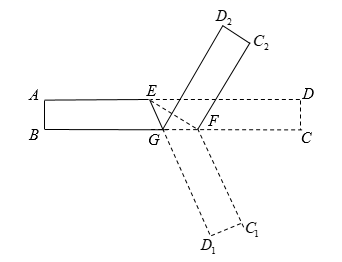 A、 B、 C、 D、9. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图所示).
A、 B、 C、 D、9. 学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图所示).
从图中可知,小敏画平行线的依据是( )
①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.
A、①或② B、②或③ C、③或④ D、①或④二、填空题(每题3分,共18分)
-
10. 如图,图①是四边形纸条 , 其中分别为上的两个点,将纸条沿折叠得到图②,若在图②中, , 则为 .
 11. 如图,在中, , , D、E分别在、上,将沿折叠得 , 且满足 , 则.
11. 如图,在中, , , D、E分别在、上,将沿折叠得 , 且满足 , 则. 12. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、 , 若 , , 则的度数是 .
12. 如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为、 , 若 , , 则的度数是 . 13. 如图所示的四种沿AB折叠纸带的方法:①如图①,展开后测得∠1=∠2;②如图②,展开后测得∠1=∠2且∠3=∠4;③如图③,测得∠1=∠2;④如图④,展开后测得∠1+∠2=180°.其中能判断纸带两条边a , b互相平行的是 . (填序号)
13. 如图所示的四种沿AB折叠纸带的方法:①如图①,展开后测得∠1=∠2;②如图②,展开后测得∠1=∠2且∠3=∠4;③如图③,测得∠1=∠2;④如图④,展开后测得∠1+∠2=180°.其中能判断纸带两条边a , b互相平行的是 . (填序号) 14. 如图1,将长方形纸带ABCD 沿EF 折叠后,点C,D分别落在点H,G 的位置,再沿 BC 折叠成图2.若∠DEF=72°,则∠GMN=°.
14. 如图1,将长方形纸带ABCD 沿EF 折叠后,点C,D分别落在点H,G 的位置,再沿 BC 折叠成图2.若∠DEF=72°,则∠GMN=°. 15. 如图,射线AB与射线CD平行,点F为射线AB上的一定点,连接CF,点P是射线CD上的一个动点(不包括端点C),将 沿PF折叠,使点C落在点E处.若 ,当点E到点A的距离最大时, .
15. 如图,射线AB与射线CD平行,点F为射线AB上的一定点,连接CF,点P是射线CD上的一个动点(不包括端点C),将 沿PF折叠,使点C落在点E处.若 ,当点E到点A的距离最大时, .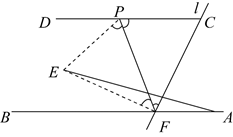
三、解答题(共4题,共31分)
-
16. 如图,直线AB∥CD,直线l与直线AB、CD相交于点E、F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
 (1)、若∠PEF=48°,点Q恰好落在其中的一条平行线上,求则∠EFP的度数;(2)、若∠PEF=75°,2∠CFQ=∠PFC,求∠EFP的度数.17. 在直角三角形ABC中, , 点D,E分别在AB,AC上,将沿DE翻折,得到.(1)、如图①,若 , 则;
(1)、若∠PEF=48°,点Q恰好落在其中的一条平行线上,求则∠EFP的度数;(2)、若∠PEF=75°,2∠CFQ=∠PFC,求∠EFP的度数.17. 在直角三角形ABC中, , 点D,E分别在AB,AC上,将沿DE翻折,得到.(1)、如图①,若 , 则;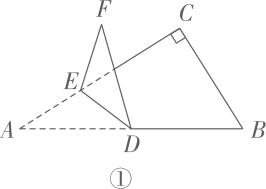 (2)、如图②,的平分线交线段BC于点G.若 , 求证.
(2)、如图②,的平分线交线段BC于点G.若 , 求证.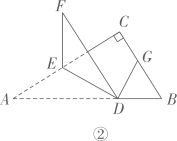 (3)、已知 , 的平分线交直线BC于点G.当的其中一条边与BC平行时,直接写出的度数(可用含a的式表示).
(3)、已知 , 的平分线交直线BC于点G.当的其中一条边与BC平行时,直接写出的度数(可用含a的式表示).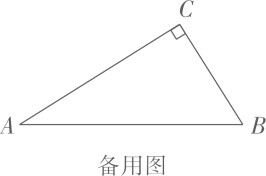 18. 如图 , 将笔记本活页一角折过去,使角的顶点落在处,为折痕
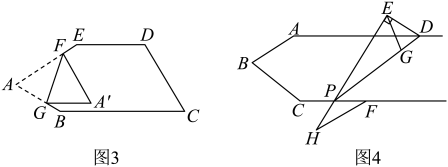
18. 如图 , 将笔记本活页一角折过去,使角的顶点落在处,为折痕 (1)、图中,若 , 求的度数;(2)、如果又将活页的另一角斜折过去,使边与重合,折痕为 , 如图所示, , 求以及的度数;(3)、如果在图中改变的大小,则的位置也随之改变,那么问题中的大小是否改变?请说明理由.19. 如图,是一张三角形的纸片,点、分别是边、上的点将沿折叠,点落在点的位置.
(1)、图中,若 , 求的度数;(2)、如果又将活页的另一角斜折过去,使边与重合,折痕为 , 如图所示, , 求以及的度数;(3)、如果在图中改变的大小,则的位置也随之改变,那么问题中的大小是否改变?请说明理由.19. 如图,是一张三角形的纸片,点、分别是边、上的点将沿折叠,点落在点的位置.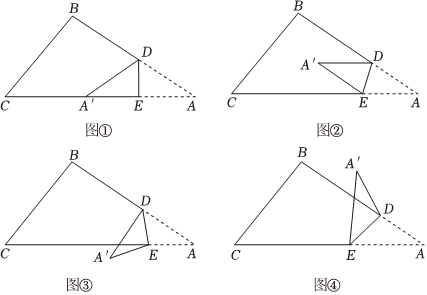 (1)、如图 , 当点落在边上时,若 , 求的大小.(2)、如图 , 当点落在内部时,若 , , 求的大小.(3)、当点落在外部时,
(1)、如图 , 当点落在边上时,若 , 求的大小.(2)、如图 , 当点落在内部时,若 , , 求的大小.(3)、当点落在外部时,如图 , 若 , , 则
如图 , 、和的数量关系为 .
四、实践探究题(共5题,共51分)
-
20. 综合与实践:折纸中的数学
【问题提出】在前面的学习中我们通过折纸可以找出一个角的平分线,还可以折出过一个点且与已知直线垂直的直线.那我们能否通过折纸的方式找到过直线外一点且与已知直线平行的直线呢?
 (1)、【知识初探】王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.
(1)、【知识初探】王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.①如图1,在纸上画出一条直线 , 在外取一点 . 过点折叠纸片,使得点的对应点落在直线上(如图2),记折痕与的交点为 , 将纸片展开铺平.则 ▲ ;
②再过点将纸片进行折叠,使得点的对应点落在直线上(如图3),再将纸片展开铺平(如图4).此时王玲说,就是的平行线.王玲的说法正确吗?请写出过程予以证明;
(2)、【拓展延伸】李强同学在王玲同学折纸的基础上,补充了条件:如图5,在线段上任取一点 , 连接 , 请你猜想与这三个角之间的数量关系,并说明理由.21. 综合与实践问题背景:
数学课上,同学们以“长方形纸带的折叠”为主题开展数学活动,已知长方形纸带的边 , , ,点 为线段AD上一动点 ,将纸片折叠,使点B和点 重合,产生折痕EF,点E是折痕与边AD的交点,点F是折痕与边BC的交点.

动手操作:
(1)、如图1,若点E与点A重合时,则 的度数为 .实践探究:
(2)、如图2,移动点 ,其余条件不变.①小静发现图中无论点 如何移动, 始终成立,请说明理由;
②小东发现折叠后所形成的角,只要知道其中一个角的度数,就能求出其它任意一角的度数,若 ,求 的大小.
22. (1)、【感知】如图①,在△ABC中, , . 则°.(2)、【操作】如图②,点D、E分别在图①中的△ABC的边AC、AB上,且均不与△ABC的顶点重合,连接DE,将△ABC沿DE折叠,使点A的对称点始终落在四边形BCDE的外部,交边AB于点F,且点与点C在直线AB的异侧.则°.(3)、求的度数.(4)、当的某条边与BC平行时,直接写出的度数.23. 同学们热爱数学,对数学知识有着自己的理解与表达.
(1)、【感知】如图①,在△ABC中, , . 则°.(2)、【操作】如图②,点D、E分别在图①中的△ABC的边AC、AB上,且均不与△ABC的顶点重合,连接DE,将△ABC沿DE折叠,使点A的对称点始终落在四边形BCDE的外部,交边AB于点F,且点与点C在直线AB的异侧.则°.(3)、求的度数.(4)、当的某条边与BC平行时,直接写出的度数.23. 同学们热爱数学,对数学知识有着自己的理解与表达. (1)、王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.
(1)、王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.①如图1,在纸上画出一条直线BC,在BC外取一点P.过点P折叠纸片,使得点C的对应点落在直线BC上(如图2),记折痕DE与BC的交点为A,将纸片展开铺平.则 ▲ .
②再过点P将纸片进行折叠,使得点E的对应点落在直线DP上(如图3),再将纸片展开铺平(如图4).此时王玲说,PF就是BC的平行线.王玲的说法正确吗?请写出过程予以证明;
(2)、李强同学在王玲同学折纸的基础上,补充了条件:如图5,连接DF交AB于点G,连接EF,并在EF上找一点H,使得 , 试判断线段HP与DF的位置关系,并说明理由.24. 在数学综合与实践课上,老师给出了下列问题:(1)、探究结论:如图1, , , 则 ▲ :如图2, , , 则 ▲

结论:两个角的两边分别平行,则这两个角 ▲ 或 ▲
(2)、应用结论:①若两个角的两边分别平行,其中一个角是另一个角的2倍少60°,则角的度数为 ▲ ;②在图3中,五边形 , 点G、F分别在、上,将∠A沿翻折得到 , , , , , 求的度数.
(3)、拓展应用:在图4中, , , , , 平分 , G点是线段上的一个动点,若中有两个相等的角, , , 直接写出的度数.