初中数学同步训练必刷培优卷(北师大版七年级下册 5.4利用轴对称进行设计)
试卷更新日期:2024-06-02 类型:同步测试
一、选择题
-
1. 如图,已知的大小为 , 是内部的一个定点,且 , 点、分别是、上的动点,若周长的最小值等于 , 则( )
 A、 B、 C、 D、2. 如图,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出( )
A、 B、 C、 D、2. 如图,在小方格中画与△ABC成轴对称的三角形(不与△ABC重合),这样的三角形能画出( ) A、1个 B、2个 C、3个 D、4个3.
A、1个 B、2个 C、3个 D、4个3.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
 A、2 B、3 C、4 D、54.
A、2 B、3 C、4 D、54.如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分)是轴对称图形,其中涂法有( )
 A、6种 B、7种 C、8种 D、9种5.
A、6种 B、7种 C、8种 D、9种5.把图形(1)叠在图形(2)上,能得到的图形可能是( )
 A、
A、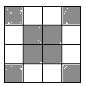 B、
B、 C、
C、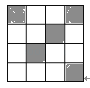 D、
D、 6.
6.如图,A、B在格点位置上,若要在所给网格中再找一个格点,使它与点A、B连成的三角形是轴对称图形,图中满足这样条件的格点共有( )个.
 A、7 B、8 C、9 D、107.
A、7 B、8 C、9 D、107.如图,在3×2的正方形网格中,已有两个小正方形被涂黑,再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的涂法有( )
 A、1种 B、2种 C、3种 D、4种8.
A、1种 B、2种 C、3种 D、4种8.如图,图2的图案是由图1中五种基本图形中的两种拼接而成,这两种基本图形是( )
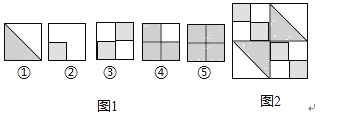 A、①② B、①③ C、①④ D、③⑤9.
A、①② B、①③ C、①④ D、③⑤9.如图,正三角形网格中,已有两个小正三角形被涂黑,随机将图中其余小正三角形涂黑一个,使整个被涂黑的图案构成一个轴对称图形的概率是( )
 A、 B、 C、 D、以上答案都不对10.
A、 B、 C、 D、以上答案都不对10.图形分割是令人困惑有趣的.比如将一个正方形分割成若干锐角三角形,要求分割的锐角三角的个数尽可能少就是让人感兴趣的问题.下图即是将正方形分割成11个、10个、9个、8个锐角三角形的图形(如图 ①~④):其中图④将正方形分割成8个锐角三角形不仅是一种巧妙的方法,而且图④还是一个轴对称图形,请找一找图④中全等三角形有( )对.
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
11. 如图,在3×3的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中的△ABC为格点三角形,在图中最多能画出个格点三角形与△ABC成轴对称.
 12. 如图,现要利用尺规作图作△ABC关于BC的轴对称图形△A′BC.若AB=5cm,AC=6cm,BC=7cm,则分别以点B、C为圆心,依次以cm、cm为半径画弧,使得两弧相交于点A′,再连结A′C、A′B,即可得△A′BC.
12. 如图,现要利用尺规作图作△ABC关于BC的轴对称图形△A′BC.若AB=5cm,AC=6cm,BC=7cm,则分别以点B、C为圆心,依次以cm、cm为半径画弧,使得两弧相交于点A′,再连结A′C、A′B,即可得△A′BC. 13. 在4×4的方格中有五个同样大小的正方形(阴影)如图摆放,移动标号为①的正方形到空白方格中,使其与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有种.
13. 在4×4的方格中有五个同样大小的正方形(阴影)如图摆放,移动标号为①的正方形到空白方格中,使其与其余四个正方形组成的新图形是一个轴对称图形,这样的移法有种. 14.
14.如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有 种.
 15.
15.如图的2×5的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有 个.

三、作图题
-
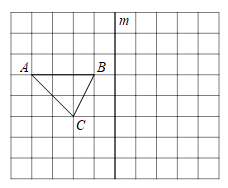
16. 如图,在边长为1的小正方形组成的网格中,点A , B , C均在小正方形的顶点上.
 (1)、 在图中画出与△ABC关于直线l成轴对称的△A′B′C′;(2)、 在直线l上找一点P , 使得△BPC的周长最小.17. 已知在同一平面内的两条相等线段,通过一次或两次轴对称变化就可以重合.如图方格纸中的每个小方格都是边长为1个单位长度的正方形,点都在格点上,请分别在下面两个图中画出对称轴,使得线段通过轴对称变化与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段.
(1)、 在图中画出与△ABC关于直线l成轴对称的△A′B′C′;(2)、 在直线l上找一点P , 使得△BPC的周长最小.17. 已知在同一平面内的两条相等线段,通过一次或两次轴对称变化就可以重合.如图方格纸中的每个小方格都是边长为1个单位长度的正方形,点都在格点上,请分别在下面两个图中画出对称轴,使得线段通过轴对称变化与线段重合;若需两次轴对称的,则要画出第一次轴对称后的对称线段.
四、解答题
-
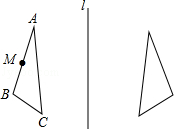
18. 如图所示,在图形中标出点A、B、C关于直线l的对称点D、E、F.若M为AB的中点,在图中标出它的对称点N.若AB=10,AB边上的高为4,则△DEF的面积为多少?
五、综合题