2024年北师大版数学七年级第二学期期末模拟试卷三
试卷更新日期:2024-06-02 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列计算正确的是( )A、 B、 C、 D、2. “燕山雪花大如席,片片吹落轩辕台.”这是诗仙李白眼里的雪花.单个雪花的重量其实很轻,只有左右,0.00003用科学记数法可表示为( )A、 B、 C、 D、3. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产作品录.下面四幅作品分别代表“惊蛰”、“谷雨”、“立秋”、“冬至”,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,下列条件中能判定AE∥CD的是( )
4. 如图,下列条件中能判定AE∥CD的是( )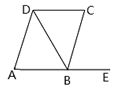 A、∠A=∠C B、∠A+∠ABC=180° C、∠C=∠CBE D、∠A=∠CBE5. 我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE.
A、∠A=∠C B、∠A+∠ABC=180° C、∠C=∠CBE D、∠A=∠CBE5. 我市为了方便市民绿色出行,推出了共享单车服务.图①是某品牌共享单车放在水平地面的实物图,图②是其示意图,其中AB,CD都与地面l平行,∠BCD=60°,∠BAC=50°,当∠MAC为( )度时,AM∥BE. A、15 B、65 C、70 D、1156. 小明家有一本200页的故事书,已知他每小时能看50页,星期天上午小明先看了故事书的一半后又做了一个小时的作业,然后他才继续看完这本书.下列能体现这本书剩下的页数y(页)与时间t(时)之间关系的是( )A、
A、15 B、65 C、70 D、1156. 小明家有一本200页的故事书,已知他每小时能看50页,星期天上午小明先看了故事书的一半后又做了一个小时的作业,然后他才继续看完这本书.下列能体现这本书剩下的页数y(页)与时间t(时)之间关系的是( )A、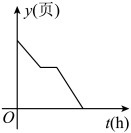 B、
B、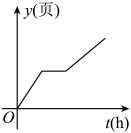 C、
C、 D、
D、 7. 县林业部门考察银杏树苗在一定条件下移植的成活率,统计银杏树苗移植成活的相关数据如下表所示:
7. 县林业部门考察银杏树苗在一定条件下移植的成活率,统计银杏树苗移植成活的相关数据如下表所示:移植的棵数
100
300
600
1000
7000
15000
成活的棵数
84
279
505
847
6337
13581
成活的频率
0.84
0.93
0.842
0.847
0.905
0.905
根据表中的信息,估计银杏树苗在一定条件下移植成活的概率为(精确到0.1)
A、0.905 B、0.90 C、0.9 D、0.88. 如图,点、、在同一直线上,若 , , , 则等于( ) A、7 B、8 C、9 D、109. 如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( )
A、7 B、8 C、9 D、109. 如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于( ) A、2cm B、3cm C、4cm D、5cm10. 如图,D,E,F分别是边BC,AD,AC上的中点,若S阴影的面积为3,则△ABC的面积是( )
A、2cm B、3cm C、4cm D、5cm10. 如图,D,E,F分别是边BC,AD,AC上的中点,若S阴影的面积为3,则△ABC的面积是( ) A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8二、填空题(每题3分,共18分)
-
11. 若2x=3,2y=5,则22x+y=.12. 若4y2+my+9是一个完全平方式,那么m的值应为 .13. 如图所示,要测量河岸相对的两点A、B之间的距离.已知AB垂直于河岸BF,在BF上取两点C、D,使CD=CB,过点D作BF的垂线ED,使A、C、E在一条直线上,若ED=90米,则AB的长是米.
 14. 如图,假设可以随意在图中取点,那么这个点取在阴影部分的概率是 .
14. 如图,假设可以随意在图中取点,那么这个点取在阴影部分的概率是 .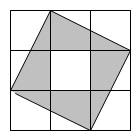 15. 如图,已知在和中,点在同一条直线上, . 请你添加一个条件 , 使得 .
15. 如图,已知在和中,点在同一条直线上, . 请你添加一个条件 , 使得 . 16. 如图,在△ABC中, , AB的垂直平分线DE交AC于D , 连结BD , 若△DBC的周长为27,则BC的长为 .
16. 如图,在△ABC中, , AB的垂直平分线DE交AC于D , 连结BD , 若△DBC的周长为27,则BC的长为 .
三、解答题(共9题,共72分)
-
17. .18. 先化简,再求值: , 其中 ,19. 先化简,再求值: , 其中 , .20. 如图,在中,于点 , 点是BC上一点,过点作于点 , 点是AC上一点,且 .
 (1)、请说明的理由.(2)、若平分 , 求的度数.21. 小明听到弟弟诵读诗句“儿童散学归来早,忙趁东风放纸鸢”时,他想借助图象大致刻画出诗句中儿童从学校放学回家,再到田野这段时间内,离家距离的变化情况.(1)、下列图象中能大致刻画这段时间儿童离家距离与时间关系的是( );A、
(1)、请说明的理由.(2)、若平分 , 求的度数.21. 小明听到弟弟诵读诗句“儿童散学归来早,忙趁东风放纸鸢”时,他想借助图象大致刻画出诗句中儿童从学校放学回家,再到田野这段时间内,离家距离的变化情况.(1)、下列图象中能大致刻画这段时间儿童离家距离与时间关系的是( );A、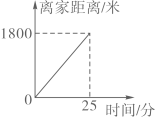 B、
B、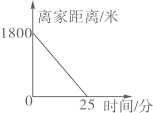 C、
C、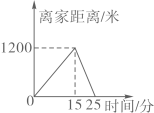 D、
D、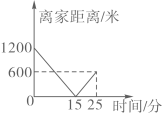 (2)、根据符合题意图象中的相关数据可知儿童家到学校的距离是米,儿童从家出发到田野所用时间为分;(3)、小明想自己动手制作风筝和弟弟一起去放,他画出了如下风筝示意图,其中 , , 他认为根据示意图,不用测量就能知道 . 你同意他的观点吗?请说明理由.
(2)、根据符合题意图象中的相关数据可知儿童家到学校的距离是米,儿童从家出发到田野所用时间为分;(3)、小明想自己动手制作风筝和弟弟一起去放,他画出了如下风筝示意图,其中 , , 他认为根据示意图,不用测量就能知道 . 你同意他的观点吗?请说明理由.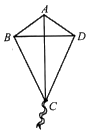 22. 如图,端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客每购买200元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针对准红、黄、绿的区域,顾客就可以分别获得50元、20元、10元的奖金,对准无色区域则无奖金(转盘被等分成16个扇形).
22. 如图,端午节期间,某商场为了吸引顾客,设立了一个可以自由转动的转盘,并规定顾客每购买200元商品,就能获得一次转动转盘的机会,如果转盘停止后,指针对准红、黄、绿的区域,顾客就可以分别获得50元、20元、10元的奖金,对准无色区域则无奖金(转盘被等分成16个扇形).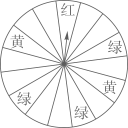 (1)、王老师购物210元,他获得奖金的概率是多少?(2)、张老师购物370元,他获得20元奖金的概率是多少?(3)、现商场想调整获得10元奖金的概率为 ,其他金额的获奖率不变,则需要将多少个无色区域涂上绿色?23. 由小正方形组成的3×3的网格中,每个小正方形的顶点称为格点.A,B,C均为格点.在给定的网格中,按下列要求画图(每小题只画一种即可):
(1)、王老师购物210元,他获得奖金的概率是多少?(2)、张老师购物370元,他获得20元奖金的概率是多少?(3)、现商场想调整获得10元奖金的概率为 ,其他金额的获奖率不变,则需要将多少个无色区域涂上绿色?23. 由小正方形组成的3×3的网格中,每个小正方形的顶点称为格点.A,B,C均为格点.在给定的网格中,按下列要求画图(每小题只画一种即可):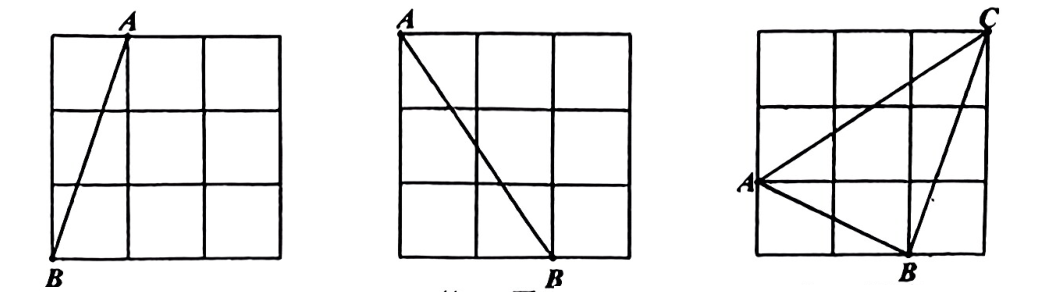
图① 图② 图③
(1)、在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N为格点.(2)、在图②中,画一条不与AB重合的线段PQ,使PQ与AB关于某条直线对称,且P,Q为格点.(3)、在图③中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D,E,F为格点.24. 已知是的平分线,点P是射线上一点,点C , D分别在射线 , 上,连接 , . (1)、【发现问题】
(1)、【发现问题】如图①,当 , 时,则与的数量关系是 .
(2)、【探究问题】如图②,点C , D在射线 , 上滑动,且 , 当时,与在【发现问题】中的数量关系还成立吗?说明理由.
25. 综合与实践问题情境:“综合与实践”课上,老师将一副直角三角板摆放在直线MN上(如图1,).保持三角板EDC不动,老师将三角板ABC绕点以每秒的速度顺时针旋转,旋转时间为秒,当AC与射线CN重合时停止旋转.各小组解决老师给出的问题,又提出新的数学问题,请你解决这些问题.
深入探究:
 (1)、老师提出,如图2,当AC转到与∠DCE的角平分线重合时,∠ECB-∠DCA=15°,当AC转到与的角平分线重合时, , 当AC在内部的其他位置时,结论是否依然成立?请说明理由.(2)、勤学小组提出:若AC旋转至的外部,与是否还存在如上数量关系?若存在,请说明理由;若不存在,请写出与的数量关系,并说明理由.(3)、拓展提升:
(1)、老师提出,如图2,当AC转到与∠DCE的角平分线重合时,∠ECB-∠DCA=15°,当AC转到与的角平分线重合时, , 当AC在内部的其他位置时,结论是否依然成立?请说明理由.(2)、勤学小组提出:若AC旋转至的外部,与是否还存在如上数量关系?若存在,请说明理由;若不存在,请写出与的数量关系,并说明理由.(3)、拓展提升:智慧小组提出:若AC旋转到与射线CM重合时停止旋转.在旋转过程中,直线DE与直线AC是否存在平行的位置关系?若存在,请直接写出的值;若不存在,请说明理由.