2024年北师大版数学七年级第二学期期末模拟试卷二

试卷更新日期：2024-06-02 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列计算正确的是（）

A、a+2a=3a² B、a²•a³=a⁵ C、a³÷a=3 D、（﹣a）³=a³

查看试题解析
2. 下列字母中不是轴对称图形的是（　　）

A、H B、E C、L D、O

查看试题解析
3. 如果9x²+kx+25是一个完全平方式，那么k的值是（）

A、15 B、±5 C、30 D、±30

查看试题解析
4. 2022年10月12日，“天宫课堂”第三课在中国空间站开讲，3名航天员演示了在微重力环境下毛细效应实验、水球变“懒”实验等，相应视频在某短视频平台的点赞量达到150万次，数据150万用科学记数法表示为（）

A、 $1.5 \times 1 0^{5}$ B、 $0.15 \times 1 0^{5}$ C、 $1.5 \times 1 0^{6}$ D、 $1.5 \times 1 0^{7}$

查看试题解析
5. 下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（）

A、2，2，5 B、3，2，6 C、1，2，2 D、1，2，3

查看试题解析
6. 如图，直线a∥b，直线c分别交a，b于点.C.∠BAC的平分线交直线b于点D，若∠2=50°，则∠1的度数是（）

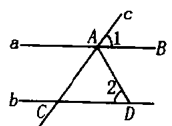A、50° B、60° C、80° D、100°

查看试题解析
7. 如图，点E在平行四边形ABCD内部， $A F ∥ B E$ ， $D F ∥ C E$ ，设平行四边形ABCD的面积为 $S_{1}$ ，四边形AEDF的面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、1 D、2

查看试题解析
8. 在边长为a的正方形中挖去一个边长为b的小正方形（ $a > b$ ）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，可以验证（）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$

查看试题解析
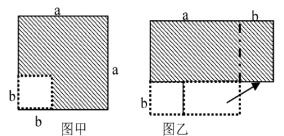9. 下列事件中，必然事件是（）

A、打开电视，正在播放宜春二套 B、抛一枚硬币，正面朝上 C、明天会下雨 D、地球绕着太阳转

查看试题解析
10. 如图，在 $▱ A B C D$ 中， $B E$ 垂直平分 $A D$ 于点E，且 $∠ B C D = 45 °$ ， $A B = 4$ ，则 $A C$ 的长为（）

A、 $3 \sqrt{2}$ B、 $2 \sqrt{5}$ C、 $3 \sqrt{5}$ D、 $4 \sqrt{5}$

查看试题解析

二、填空题（每题3分，共18分）

11. 已知 $a^{m} = 3$ ， $a^{n} = 7$ ，则 $a^{m + n} =$ ．

查看试题解析
12.
如图，点B、A、D、E在同一直线上，BD=AE，BC∥EF，要使△ABC≌△DEF，则只需添加一个适当的条件是．（只填一个即可）

查看试题解析
13. 等腰三角形的一个角是100°，则它的底角度数是°.

查看试题解析
14. 如图，小明从点A向北偏东70°方向走到B点，又从B点向北偏西30°方向走到点C，则∠ABC的度数为°．

查看试题解析
15. 如图，直线AB，CD相交于点0，OE平分∠AOD，若∠BOC=80°，则∠AOE=°．

查看试题解析
16. 已知关于x，y的方程2x+y﹣1＝0，用含x的式子表示y为．

查看试题解析

三、解答题（共9题，共72分）

17. 计算：(- 2a²b³)·(-3a)·(-2c)．

查看试题解析
18. 先化简，再求值： $[(2 x - y) (2 x + y) - (x - y)^{2} + 2 y^{2}] \div 2 x$ ，其中 $x = 2$ ， $y = - 3$

查看试题解析
19. 已知2a-b=7，求代数式[a²+b²-（a-b）²+2b（a-b）]÷（4b）的值。

查看试题解析
20. 如图，在 $3 \times 3$ 的正方形网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，如图三个图中的三角形为格点三角形，在图中分别画出与已知三角形成轴对称 $($ 对称轴不相同 $)$ 的格点三角形．

查看试题解析
21. 小亮和小芳都想参加学校杜团组织的暑假实践活动，但只有一个名额，小亮提议用如下的办法决定谁去等加活动：将一个转盘9等分，分别标上1至9九个号码，随意转动转盘，若转到2的倍数，小亮去参加活动；转到3的倍数，小芳去参加活动；转到其它号码则重新特动转盘．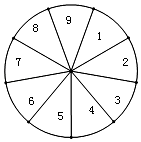

(1)、转盘转到2的倍数的概率是多少？

(2)、你认为这个游戏公平吗？请说明理由．

查看试题解析

22. 由于惯性的作用，行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”

.

为了测定某种型号小型载客汽车的刹车性能

(

车速不超过

140 k m / h)

，对这种型号的汽车进行了测试，测得的数据如下表：

刹车时车速 $v (k m / h)$	$0$	$10$	$20$	$30$	$40$	$50$	$\dots$
刹车距离 $s (m)$	$0$	$2.5$	$5$	$7.5$	$10$	$12.5$	$\dots$

请回答下列问题：

(1)、在这个变化过程中，自变量是，因变量是；

(2)、当刹车时车速为

60 k m / h

时，刹车距离是

m

；

(3)、根据上表反映的规律写出该种型号汽车

s

与

v

之间的关系式：；

(4)、该型号汽车在高速公路上发生了一次交通事故，现场测得刹车距离为

32 m

，推测刹车时车速是多少？并说明事故发生时，汽车是超速行驶还是正常行驶？

$($ 相关法规： $《$ 道路交通安全法 $》$ 第七十八条：高速公路上行驶的小型载客汽车最高车速不得超过每小时 $120$ 公里 $.)$

查看试题解析

23. 如图，AB∥CD，E是CD上一点，AE交BC于点F，且∠ABE=∠DBC，∠ABC=∠AEB。

(1)、试判断AE与BD的位置关系，并说明理由。

(2)、若BE平分∠CBD，∠AEB=40°，求∠D的度数。

查看试题解析
24. 如图所示，∠ABD和∠BDC的平分线交于点E，BE交CD于点F，∠1+∠2=90°．

(1)、求证：AB∥CD；

(2)、试猜想∠2与∠3的数量关系，并说明理由．

查看试题解析
25. 如图， $A B = A C$ ， $C E ∥ A B$ ， D是 $A C$ 上的一点，且 $A D = C E$ .

(1)、求证： $△ A B D ≌ △ C A E$

(2)、若 $∠ A B D = 25 °$ ， $∠ C B D = 40 °$ ，求 $∠ B A E$ 的度数.

查看试题解析