命题新趋势9 方案设计——2024年浙教版数学八（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、解答题

1. 现有一个用铁网围成的长、宽之比为3：1的猪舍，需将面积扩大 $\frac{1}{3}$ ，方案有两种．方案一：再另外单独围一个正方形猪舍；方案二：将原猪舍改成正方形猪舍．请你参谋一下，你认为哪个方案比较好？为什么？

查看试题解析
2. 如图，在一块长为16m 、宽为12m的长方形荒地上，要建造一个花园，要求花园面积是原荒地面积的一半，下面分别是小华与小芳的设计方案. 同学们都认为小华的方案是正确的，但对小芳的方案是否符合条件有不同意见，你认为小芳的方案符合条件吗？若不符合，请用解方程的方法说明理由.

查看试题解析

二、实践探究题

3. 综合实践：

项目主题	“亚运主题”草坪设计
项目情境	为了迎亚会，同学们参与一块长为40米，宽为30米的矩形“亚运主题”草坪方案设计的项目学习．以下为项目学习小组对草坪设计的研究过程．
活动任务一	请设计两条相同宽度的小路连接矩形草坪两组对边．小组内同学们设计的方案主要有甲、乙、丙、丁四种典型的方案
驱动问题一	（1）项目小组设计出来的四种方案小路面积的大小关糸？ ①直观猜想：我认为 ▲ ；（请用简洁的语言或代数式表达你的猜想） ②具体验证：选择最简单的甲、乙方案，假设小路宽为1米，则甲、乙方案中小路的面积分别为 ▲ 和 ▲ ； ③一般验证：若小路宽为x米，则甲、乙方案中小路所占的面积分别为 ▲ 和 ▲ ．
活动任务二	为施工方便，学校选择甲种方案设计，并要求除小路后草坪面积约为1064平方米．
驱动问题二	（2）请计算两条小路的宽度是多少？
活动任务三	为了布置五环标志等亚运元素，将在草坪上的亚运宣传主题墙前，用篱笆围（三边）成面积为100平方米的矩形 $A B C D$ ，如图．
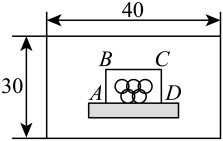
驱动问题三	（3）为了使篱笆恰好用完同时围住三面，项目小组的同学对下列问题展开探究，其中矩形宽 $A B = x$ ，长 $B C = y$ ． ①若30米长的篱笆，请用两种不同的函数表示y关于x的函数关系． ②数学之星小明提出一个问题：若a米长的篱笆恰好用完，且有两种不同方案可以选择，使得两种方案的宽之和小于15米，甲同学说“篱笆的长可以是28米”，乙同学说“篱笆的长可以是32米”，你认为他们俩的说法对吗？请说明理由．

查看试题解析

4. 根据素材，探索完成任务．

如何裁剪出符合要求的长方形彩纸？
素材1	图1是一张等腰直角三角形彩纸， $A C = B C = 30 c m$ ．甲、乙、丙三名同学分别用这样的彩纸试图截前出不一样的长方形，并使长方形的四个顶点都在 $△ A B C$ 的边上．
素材2	甲同学按图2的方式栽剪，想裁出两边长之比为 $1 ： 2$ 的长方形；乙同学按图3的方式裁剪，想裁出面积为 $125 {cm}^{2}$ 的长方形；丙同学想裁出面积最大的正方形．
问题解决
任务1	请帮助甲同学计算此长方形面积
任务2	请求出符合乙同学裁剪方案的方形的长与宽．
任务3	请帮助丙同学在图4和图5中各画出一种裁剪方案，并通过计算说明哪种方案裁得的正方形面积最大

查看试题解析

5. 【综合与实践】数学来源于生活，同时数学也可以服务于生活.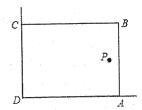
【知识背景】如图，校园中有两面直角围墙，墙角内的P处有一古棵树与墙 $C D$ ， $A D$ 的距离分别是 $15 m$ 和 $6 m$ ，在美化校园的活动中，某数学兴趣小组想借助围墙（两边足够长），用 $28 m$ 长的篱笆围成一个矩形花园 $A B C D$ （篱笆只围 $A B$ ， $B C$ 两边），设 $A B = x m$ .
【方案设计】设计一个矩形花园，使之面积最大，且要将古棵树P围在花园内（含边界，不考虑树的粗细）.
【解决问题】思路：把矩形 $A B C D$ 的面积S与边长x（即 $A B$ 的长）的函数解析式求出，并利用函数的性质来求面积的最大值即可.

(1)、请用含有x的代数式表示 $B C$ 的长；

(2)、花园的面积能否为 $192 m^{2}$ ?若能，求出x的值，若不能，请说明理由；

(3)、求面积S与x的函数解析式，写出x的取值范围；并求当x为何值时，花园面积S最大?

查看试题解析

6. 党的二十大报告指出大自然是人类赖以生存发展的基本条件……垃圾分类、节能减排、废物再利用等必须从我们身边小事做起.为了充分利用四边形余料，小明设计了不同的方案裁剪正方形，裁剪方案与数据如下表：

方案设计	方案1	方案2
裁剪方案示意图
说明	图中的正方形 $E F B G$ 和正方形 $M N P Q$ 四个顶点都在原四边形的边上
测量数据	$A D = 3 d m$ ， $A B = 9 d m$ ， $C B = 12 d m$ ， $∠ A = ∠ B = 90 °$
任务1：探寻边长关系	填空： $C D =$ ▲ dm； $\frac{P N}{B N}$ = ▲
任务2：比较面积大小	计算或推理：比较正方形 $E F B G$ 和正方形 $M N P Q$ 边长的大小
任务3：应用实践	若在四边形 $A D Q P$ 余料上再截取一个最大正方形，正方形的边长为 ▲

查看试题解析

7. 根据以下信息，探索完成任务．

如何设计种植方案？

素材1

小明以“种植农作物”为主题在自己家100平方米的土地上进行课外实践，现有A、B两种作物的相关信息如下表所示：

	A作物	B作物
每平方米种植株树(株)	2	10
单株产量(千克)	1.2	0.5

素材2

由于A作物植株间距较大，可增加A作物每平方米的种植株树．经过调研发现，每平方米种植A作物每增加1株，A作物的单株产量减少0.1千克．

素材3

若同时种植A、B两种作物，实行分区域种植．

问题解决

单一种植(全部种植A作物)

任务1：明确数量关系

设每平方米增加x株A作物(x 为正整数)，则每平方米有 ▲ 株，单株产量为 ▲ 千克．(用含x的代数式表示)

任务2：计算产量

要使A作物每平方米产量为4.8千克，则每平方米应种植多少株？

单一种植(全部种植A作物)

任务3：规划种植方案

设这100平方米的土地中有a平方米用于种植A作物，且每平方米产量最大，其余区域按照每平方米10株种植B作物，当这100平方米总产量不低于496千克时，则a的取值范围是 ▲

查看试题解析

8. 先阅读下列材料，再解答问题．

尺规作图：

已知： $△ A B C$ ， D是边 $A B$ 上一点，如图1．

求作：四边形 $D B C F$ ，使得四边形 $D B C F$ 是平行四边形．

小明的做法如下：

⑴设计方案

先一个正确的草图，如图2，

再分析实现目标的具体方法．

⑵设计作图步骤，完成作图

作法：如图3，

①以点C为圆心、 $B D$ 为半径画弧；

②再以点D为圆心、 $B C$ 为半径画弧，两弧交于点F；

③连接 $D F$ 与 $C F$ ．

∴四边形 $D B C F$ 即为所求．

请在图3中完成尺规作图，保留作图痕迹

⑶推理论证

证明：∵ ，

∴四边形DBCF是平行四边形．（）（填推理依据）

查看试题解析

9. 【问题背景】
如图1，数学实践课上，学习小组进行探究活动，老师要求大家对矩形 $A B C D$ 进行如下操作：①分别以点 $B ， C$ 为圆心，以大于 $\frac{1}{2} B C$ 的长度为半径作弧，两弧相交于点 $E$ ， $F$ ，作直线 $E F$ 交 $B C$ 于点 $O$ ，连接 $A O$ ；②将 $△ A B O$ 沿 $A O$ 翻折，点 $B$ 的对应点落在点 $P$ 处，作射线 $A P$ 交 $C D$ 于点 $Q$ ．

【问题提出】
在矩形 $A B C D$ 中， $A D = 5 ， A B = 3$ ，求线段 $C Q$ 的长．
【问题解决】
经过小组合作、探究、展示，其中的两个方案如下：
方案一：连接 $O Q$ ，如图2．经过推理、计算可求出线段 $C Q$ 的长；
方案二：将 $△ A B O$ 绕点 $O$ 旋转 $180 °$ 至 $△ R C O$ 处，如图3．经过推理、计算可求出线段 $C Q$ 的长．
请你任选其中一种方案求线段 $C Q$ 的长．

查看试题解析