命题新趋势7 阅读理解——北师大版数学七（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 请阅读以下“预防近视”知识卡

已知如上图，桌面和水平面平行， $C D$ 与书本所在平面重合，根据卡片内容，请判断正常情况下，坐姿正确且座椅高度适合时，视线 $B C$ 和书本所在平面所成角度 $∠ B C D$ 不可能为以下哪个角度（）

A、 $74 °$ B、 $78 °$ C、 $84 °$ D、 $88 °$

查看试题解析

二、作图题

2. 阅读下列材料，回答问题．
如图1，小明将三角形纸片 $A B C$ 折叠，使点 $B$ 和 $C$ 重合，折痕为 $D E$ ，连接 $A D$ ，展开纸片后小明认为 $△ A B D$ 和 $△ A C D$ 的面积相等．理由如下：
由折叠知， $B D = C D$ ．
过点 $A$ 作 $A F ⊥ B C$ 于点 $F$ ， $S_{△ A B D} = \frac{1}{2} B D \cdot A F$ ， $S_{△ A C D} = \frac{1}{2} C D \cdot A F$ ，所以 $S_{△ A B D} = S_{△ A C D}$ ．
请你根据以上信息，利用无刻度的直尺和圆规将图2中的三角形分为面积相等的两个三角形．

查看试题解析

三、解答题

3. 阅读下列各式： ${(a \cdot b)}^{2} = a^{2} b^{2}, {(a \cdot b)}^{3} = a^{3} b^{3}, {(a \cdot b)}^{4} = a^{4} b^{4}$ ， ……．
请回答下列问题：

(1)、计算： ${(2 \times \frac{1}{2})}^{100} =$ ， $2^{100} \times {(\frac{1}{2})}^{100} =$ ．

(2)、通过上述规律，归纳得出： ${(a \cdot b)}^{n} =$ ； ${(a \cdot b \cdot c)}^{n} =$ ．

(3)、请应用上述性质计算： ${(- 0.125)}^{2025} \times 2^{2024} \times 4^{2023}$ ．

查看试题解析
4. 阅读下面的材料：
$\frac{1}{2} \times \frac{3}{2} = (1 - \frac{1}{2}) (1 + \frac{1}{2}) = 1 - \frac{1}{2^{2}}$ ；
$\frac{2}{3} \times \frac{4}{3} = (1 - \frac{1}{3}) (1 + \frac{1}{3}) = 1 - \frac{1}{3^{2}}$ ；
……
利用上面材料中的方法解答下列各题：

(1)、① $\frac{3}{4} \times \frac{5}{4} = (1 - \frac{1}{4}) (1 + \frac{1}{4}) = 1 -$ ；
② $\frac{6}{7} \times \frac{8}{7} =$ $= 1 -$ ；

(2)、计算： $(1 - \frac{1}{5}) \times (1 + \frac{1}{5}) \times (1 + \frac{1}{5^{2}}) \times (1 + \frac{1}{5^{4}}) + \frac{1}{5^{8}}$ ．

查看试题解析
5. 阅读理解，补全证明过程及推理依据．
已知：如图，点 $E$ 在直线 $D F$ 上，点 $B$ 在直线 $A C$ 上， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．
求证： $∠ A = ∠ F$
证明： $∵ ∠ 1 = ∠ 2$ （已知）
$∠ 2 = ∠ D G F$ （    ），
$∴ ∠ 1 = ∠ D G F$ （等量代换），
$∴$     ▲     $/ /$ $∴$     ▲    （    ），
$∴ ∠ 3 + ∠$ $∴$     ▲     $= 180 °$ （    ），
又 $∵ ∠ 3 = ∠ 4$ （已知），
$∴ ∠ 4 + ∠ C = 180 °$ （等量代换），
$∴$ $∴$     ▲     $/ /$ $∴$     ▲    （    ），
$∴ ∠ A = ∠ F$ （    ）．

查看试题解析
6. 先阅读后作答：根据几何图形的面积关系可以说明一些等式成立，例如：(2a+b)(a+b)=2a²+3ab+b² ，就可以用图①的面积关系来说明。

(1)、根据图②写出一个等式：

(2)、已知等式：(x+1)(x+3)=x²+4x+3，请你画出一个相应的几何图形加以说明．(仿照图①或图②画出图形即可)．

查看试题解析

四、综合题

7. 阅读下列材料，并补充完整，然后解答问题

(1)、试比较 $3^{55} ， 4^{44} ， 5^{33}$ 的大小，并完成填空
解： $3^{55} = {3^{11}}^{\times 5} = (3^{5})^{11} =$ （）¹¹ ，同理： $4^{44} =$ （）¹¹ ， $5^{33} =$ （）¹¹
因为：当底数大于1，指数大于1且相同时，底数越大，幂就越大．所以：＜＜．

(2)、请利用上述解题思路比较 $2^{125} ， 3^{100} ， 4^{75}$ 的大小．

查看试题解析
8. 阅读下列各式：（ab）²＝a²b² ，（ab）³＝a³b³ ，（ab）⁴＝a⁴b⁴…

(1)、归纳得（ab）n＝；（abc）n＝；

(2)、计算4¹⁰⁰×0.25¹⁰⁰＝；（ $\frac{1}{2}$ ）⁵×3⁵×（ $\frac{2}{3}$ ）⁵＝；

(3)、应用上述结论计算： ${(- 0.125)}^{2017} \times 2^{2018} \times 4^{2016}$ 的值.

查看试题解析
9. 阅读下面的材料，并解决问题

(1)、已知在△ABC中，∠A=60°，图1-3的△ABC的内角平分线或外角平分线交于点O，
请直接写出下列角度的度数，
如图1，∠O＝；如图2，∠O＝；如图3，∠O＝；

(2)、如图4，点O是△ABC的两条内角平分线的交点，求证：∠O＝90°+ $\f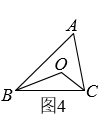rac{1}{2}$ ∠A

(3)、如图5，在△ABC中，∠ABC的三等分线分别与∠ACB的平分线交于点O₁O₂ ，若∠1＝115°，∠2＝135°，求∠A的度数．

查看试题解析
10. 阅读理解，自主探究：
“一线三垂直”模型是“一线三等角”模型的特殊情况，即三个等角角度为90°，于是有三组边相互垂直．所以称为“一线三垂直模型”．当模型中有一组对应边长相等时，则模型中必定存在全等三角形．

(1)、问题解决：如图1，在等腰直角 $△ A B C$ 中， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，过点C作直线 $D E$ ， $A D ⊥ D E$ 于D， $B E ⊥ D E$ 于E，求证： $△ A D C ≌ △ C E B$ ；

(2)、问题探究：如图2，在等腰直角 $△ A B C$ 中， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，过点C作直线 $C E$ ， $A D ⊥ C E$ 于D， $B E ⊥ C E$ 于E， $A D ＝ 2.5$ cm， $D E ＝ 1.7$ cm，求 $B E$ 的长；

(3)、拓展延伸：如图3，在平面直角坐标系中， $A （ - 1 ， 0 ）， C （ 1 ， 3 ）$ ， $△ A B C$ 为等腰直角三角形， $∠ A C B ＝ 90 °$ ， $A C ＝ B C$ ，求B点坐标．

查看试题解析
11. 阅读理解：如图 $1$ ，已知点 $A$ 是 $B C$ 外一点，连接 $A B$ ， $A C .$ 求 $∠ B A C + ∠ B + ∠ C$ 的度数．

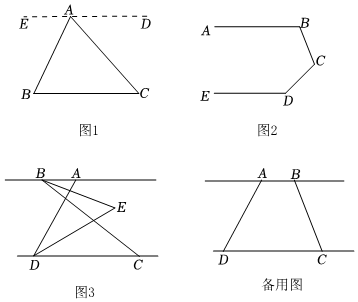(1)、阅读并补充下面推理过程．
解：过点 $A$ 作 $E D / / B C$ ， $∴ ∠ B =$ ， $∠ C =$ ．

$∵ ∠ E A B + ∠ B A C + ∠ D A C = 180 °$ ．

$∴ ∠ B + ∠ B A C + ∠ C = 180 °$ ．

解题反思：从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将 $∠ B A C$ ， $∠ B$ ， $∠ C$ “凑”在一起，得出角之间的关系，使问题得以解决．

(2)、方法运用：如图2，已知 $A B / / E D$ ，求 $∠ B + ∠ B C D + ∠ D$ 的度数．

(3)、深化拓展：如图3，已知 $A B / / C D$ ，点 $C$ 在点 $D$ 的右侧， $∠ A D C = 60 °$ ， $D E$ 平分 $∠ A D C$ ，点 $B$ 是直线 $A B$ 上的一个动点（不与点 $A$ 重合）， $A B < C D$ ， $B E$ 平分 $∠ A B C$ ， $B E$ ， $D E$ 所在的直线交于点 $E$ ，点 $E$ 在 $A B$ 与 $C D$ 两条平行线之间．若 $∠ A B C = n °$ ，请你直接写出 $∠ B E D$ 的度数．（用含 $n$ 的代数式表示）.

查看试题解析
12. 阅读下列材料并解答问题：在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“梦想三角形”例如：一个三角形三个内角的度数分别是120°，40°，20°，这个三角形就是一个“梦想三角形”.反之，若一个三角形是“梦想三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.

(1)、如果一个“梦想三角形”有一个角为108°，那么这个“梦想三角形”的最小内角的度数为

(2)、如图1，已知∠MON＝60°，在射线OM上取一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（点C不与O、B重合），若∠ACB=80°.判定△AOB、△AOC是否是“梦想三角形”，为什么？

(3)、如图2，点D在△ABC的边上，连接DC，作∠ADC的平分线交AC于点E，在DC上取一点F，使得∠EFC+∠BDC＝180°，∠DEF＝∠B.若△BCD是“梦想三角形”，求∠B的度数.

查看试题解析

五、实践探究题

13. 阅读下列材料，解决相应问题．

(1)、【学科融合】如图1，物理学光的反射现象中，把经过入射点 $O$ 并垂直于反射面的直线 $O N$ 叫做法线，入射光线与法线的夹角 $i$ 叫做入射角，反射光线与法线的夹角 $r$ 叫做反射角，反射角 $r =$ 入射角 $i$ ，这就是光的反射定律．
在图1中，证明 $∠ 1 = ∠ 2$ ；

(2)、【问题解决】根据光的反射定律，人们制造了潜望镜，如图2是潜望镜的工作原理示意图， $A B$ 、 $C D$ 是平行放置的两面平面镜， $E F$ 是射入潜望镜的光线， $G H$ 是经平面镜两次反射后离开潜望镜的光线，由可知，光线经过平面镜反射时，有 $∠ 2 = ∠ 1$ ， $∠ 4 = ∠ 5$ ；
①请问 $∠ 2$ 和 $∠ 5$ 有什么关系？并说明理由；
②请问光线 $E F$ 和 $G H$ 是否平行？并说明理由．

查看试题解析
14. 阅读材料，并解答下列问题：
我们知道，利用图形面积的不同计算方法，有些几何图形能直观地反应某些恒等式的对应关系．
例如：

(1)、如图1，反应的是a²+2ab+b²= ．

(2)、如图2，反应的是a²-b²= ．

(3)、如图3，反应的是2a²+3ab+b²= ．

查看试题解析
15. 阅读材料：
我们已经知道，根据几何图形的面积关系可以说明(a+n)(b+m)=ab+am+nb+mn.实际上还有一些等式也可以用这种方式加以说明，例如： $(2 a + b) (a + b) = 2 a^{2} + 3 a b + b^{2}$ 就可以用图1的面积关系来说明。
解答问题：

(1)、根据图2写出一个等式：.

(2)、已知等式： $(x + 1) (x + 3) = x^{2} + 4 x + 3 ，$ 请你画出一个相应的几何图形加以说明(仿照图1或图2画出图形即可).

查看试题解析
16. 【阅读理解】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，基于此，请解答下列问题：

(1)、【类比应用】①若 $x y = 8$ ， $x + y = 6$ ，则 $x^{2} + y^{2}$ 的值为；
②若 $x (5 - x) = 6$ ，则 $x^{2} + {(5 - x)}^{2} =$ ；

(2)、【迁移应用】两块完全相同的特制直角三角板 $(∠ A O B = ∠ C O D = 90 °)$ 如图2所示放置，其中 $A$ ， $O$ ， $D$ 在一直线上，连接 $A C$ ， $B D$ ，若 $A D = 14$ ， $S_{Δ A O C} + S_{Δ B O D} = 54$ ，求一块三角板的面积．

查看试题解析
17. 【阅读理解】课外兴趣小组活动时，老师提出了如下问题：如图1， $△ A B C$ 中， $A B = 8$ ， $A C = 6$ ，求 $B C$ 边上的中线 $A D$ 的取值范围.
经过组内合作交流，小明得到了如下的解决方法：延长 $A D$ 到点E ，使 $D E = A D$ .请根据小明的方法思考：

(1)、请证明 $△ A D C ≌ △ E D B$

(2)、请直接写出 $A D$ 的取值范围 $< A D <$ ；

(3)、【问题解决】请利用上述方法（倍长中线）解决问题.
如图2，已知 $∠ B A C + ∠ C D E = 180 °$ ， $A B = A C$ ， $D C = D E$ ， P为 $B E$ 的中点.若A ， C ， D共线，求证： $A P$ 平分 $∠ B A C$ ；

查看试题解析
18. 阅读理解：
若x满足 $(210 - x) (x - 200) = - 204$ ，试求 ${(210 - x)}^{2} + {(x - 200)}^{2}$ 的值，
解：设 $(210 - x) = a$ ， $(x - 200) = b$ ，则 $a b = - 204$ ，且a＋b＝(210－x)＋(x－200)＝10，
∵ ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，
∴ $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 1 0^{2} - 2 \times (- 204) = 508$ ，即 ${(210 - x)}^{2} + {(x - 200)}^{2}$ 的值为 $508$ ．
解决问题

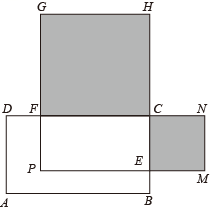(1)、若x满足 $(2022 - x) (x - 2010) = 22$ ，则 ${(2022 - x)}^{2} + {(x - 2010)}^{2} =$ ；

(2)、若(2022－x)²＋(x－2002)²＝2020，求 $(2022 - x) (x - 2002)$ 的值；

(3)、如图，在长方形ABCD中，AB＝10，BC＝6，点E ， F分别是BC ， CD上的点，且BE＝DF＝x ，分别以FC ， CE为边在长方形ABCD外侧作正方形CFGH 和CEMN ，若长方形CEPF的面积为40平方单位，则图中阴影部分的面积和为多少？

查看试题解析
19. 阅读与思考
下面是小明同学的数学学习笔记，请您仔细阅读并完成相应的任务：构造全等三角形解决图形与几何问题

在图形与几何的学习中，常常会遇到一些问题无法直接解答，需要添加辅助线才能解决．比如下面的题目中出现了角平分线和垂线段，我们可以通过延长垂线段与三角形的一边相交构造全等三角形，运用全等三角形的性质解决问题．

例：如图1， $D$ 是 $△ A B C$ 内一点，且 $A D$ 平分 $∠ B A C$ ， $C D ⊥ A D$ ，连接 $B D$ ，若 $△ A B D$ 的面积为10，求 $△ A B C$ 的面积．

该问题的解答过程如下：

解：如图2，过点 $B$ 作 $B H ⊥ C D$ 交 $C D$ 延长线于点 $H$ ， $C H$ 、 $A B$ 交于点 $E$ ，

      $∵ A D$ 平分 $∠ B A C$ ，

      $∴ ∠ D A B = ∠ D A C$ ．

      $∵ A D ⊥ C D$ ，

      $∴ ∠ A D C = ∠ A D E = 90 °$ ．

在 $△ A D E$ 和 $△ A D C$ 中， ${\begin{array}{l} ∠ D A E = ∠ D A C \\ A D = A D \\ ∠ A D E = ∠ A D C \end{array}$ ，

      $∴ △ A D E ≌ △ A D C$ （依据1）

$∴ E D = C D$ （依据2）， $S_{△ A D E} = S_{△ A D C}$ ，

      $∵ S_{△ B D E} = \frac{1}{2} D E \cdot B H$ ， $S_{△ B D C} = \frac{1}{2} C D \cdot B H$ ．

……

(1)、任务一：上述解答过程中的依据1，依据2分别是，；

(2)、任务二：请将上述解答过程的剩余部分补充完整；

(3)、应用：如图3，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ， $B E$ 平分 $∠ C B A$ 交 $A C$ 于点 $D$ ，过点 $C$ 作 $C E ⊥ B D$ 交 $B D$ 延长线于点 $E$ ．若 $C E = 6$ ，求 $B D$ 的长．

查看试题解析
20. 阅读材料：两个三角形各有一个角互为对顶角，这两个三角形叫做对顶三角形.
解决问题：如图， $△ A O D$ 与 $△ B O C$ 是对顶三角形.

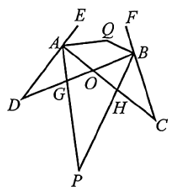(1)、试说明： $∠ D A O + ∠ D = ∠ O B C + ∠ C$ ；

(2)、试利用上述结论解决下列问题：
若 $A P$ 、 $B P$ 分别平分 $∠ D A C$ 与 $∠ D B C$ ， $∠ C = m °$ ， $∠ D = n °$ ，

①求 $∠ P$ 的度数（用含m、n的代数式表示）；

②若 $A Q$ 、 $B Q$ 分别平分 $∠ E A C$ 与 $∠ D B F$ ， $120 ° \leq ∠ Q \leq 150 °$ ，求 $m + n$ 的取值范围.

查看试题解析
21. 【阅读材料】
在“相交线与平行线”的学习中，有这样一道典型问题：

如图①，AB∥CD，点P在AB与CD之间，可得结论：∠BAP+∠APC+∠PCD=360°．

理由如下：

过点P作PQ∥AB．

∴∠BAP+∠APQ=180°．

∵AB∥CD，

∴PQ∥CD．

∴∠PCD+∠CPQ=180°．

∴∠BAP+∠APC+∠PCD

=∠BAP+∠APQ+∠CPQ+∠PCD

=180°+180°

=360°．

【问题解决】

(1)、如图②，AB∥CD，点P在AB与CD之间，写出∠BAP，∠APC，∠PCD间的等量关系；（只写结论）

(2)、如图③，AB∥CD，点P，E在AB与CD之间，AE平分∠BAP，CE平分∠DCP．写出∠AEC与∠APC间的等量关系，并说明理由；

(3)、如图④，AB∥CD，点P，E在AB与CD之间，∠BAE= $\frac{1}{3}$ ∠BAP，∠DCE= $\frac{1}{3}$ ∠DCP，写出∠AEC与∠APC间的等量关系．（只写结论）

查看试题解析
22. 请解答下列各题：
（1）阅读并回答：科学实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等．如图1，一束平行光线 $A B$ 与 $D E$ 射向一个水平镜面后被反射，此时 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ．
①由条件可知： $∠ 1 = ∠ 3$ ，依据是                     ， $∠ 2 = ∠ 4$ ，依据是                     ．
②反射光线 $B C$ 与 $E F$ 平行，依据是                     ．
（2）解决问题：如图2，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射到平面镜 $b$ 上，又被 $b$ 镜反射，若 $b$ 射出的光线 $n$ 平行于 $m$ ，且 $∠ 1 = 42 °$ ，则 $∠ 2 =$                     ； $∠ 3 =$                      ．

查看试题解析