命题新趋势7 阅读理解——2024年浙教版数学八(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、实践探究题
-
1. 阅读下列文字,回答问题.
题目:在Rt中, , 则 .
证明:假设 , 因为 , 所以 .
所以 , 这与假设矛盾,所以 .
上面的证明有没有错误?若没有错误,指出其证明的方法;若有错误,请予以纠正.
2. 阅读下列解题过程:根据上述解法简化下列各式:
(1)、 .
(2)、 .3. 阅读下列解题过程:,
.
请回答下列问题:
(1)、观察上面的解答过程,请写出;(2)、请你用含(为正整数)的关系式表示上述各式子的变形规律:;(3)、利用上面的解法,请化简: .4. 阅读材料并解答问题:∵
反之
∴
(1)、化简:.(2)、若则m,n与a,b之间存在怎样的等量关系?请说明理由.(3)、已知求的值5. 阅读材料,并解决问题:定义:将分母中的根号化去的过程叫做分母有理化.如:将分母有理化,解:原式 .
运用以上方法解决问题:
已知: , .
(1)、化简m , n;(2)、求的值.6. 【阅读理解】爱思考的小名在解决问题:已知 , 求的值.他是这样分析与解答的:
∵ , .
∴ , 即.
∴.
∴.
请你根据小名的分析过程,解决如下问题:
(1)、计算:.(2)、计算的值.(3)、若 , 求的值.7. 阅读材料:我们把形如 (其中a是常数且a≥0)这样的方程叫做x的完全平方方程.如 都是完全平方方程.
那么如何求解完全平方方程呢?我们可以利用“乘方运算”把二次方程转化为一次方程进行求解.如:解完全平方方程. 由 =9可得 .
解决下列问题:(1)、解方程:解:根据乘方运算,得 3x-2=5,或3x-2=
分别解这两个一元一次方程,得
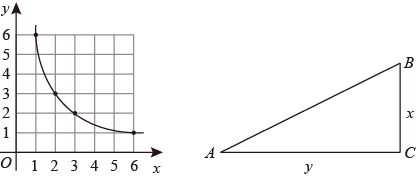
(2)、解方程:8. 阅读材料:已知:一次函数y=﹣x+b与反比例函数y= (x>0),当两个函数的图象有交点时,求b的取值范围.
 (1)、方方给出了下列解答:
(1)、方方给出了下列解答:﹣x+b=
x2﹣bx+4=0
∵两个函数有交点
∴△=b2﹣16≥0
但是方方遇到了困难:利用已学的知识无法解b2﹣16≥0这个不等式;
此时,圆圆提供了另一种解题思路;
第1步:先求出两个函数图象只有一个交点时,b= ▲ ;
第2步:画出只有一个交点时两函数的图象(请帮圆圆在直角坐标系中画出图象);
第3步:通过平移y=﹣x+b的图象,观察得出两个函数的图象有交点时b的取值范围是 ▲ .
应用:
如图,Rt△ABC中,∠C=90°,BC的长为x,AC的长为y,且S△ABC=12.
(2)、求y关于x的函数表达式;(3)、设x+y=m,求m的取值范围.9. 阅读材料:一些含根号的式子可以写成另一个式子的平方,如
设(其中a,b,m,n均为正整数),则有
这样可以把部分形如a+b 的式子化为完全平方式.
请你仿照上述方法探索并解决下列问题:
(1)、当a,b,m,n均为正整数时,若用含 m,n的式子分别表示a,b,a= , b=(2)、利用所探索的结论,找一组正整数 a,b,m,n'填空+ = (+ )2(3)、化简.10. 先阅读下面的例题,再按要求解答下列问题:求代数式y2+4y+8的最小值.
解:y2+4y+8=y2+4y+4+4=(y+2)2+4,
∵(y+2)2≥0,
∴(y+2)2+4≥4
∴y2+4y+8的最小值是4.
(1)、求代数式m2+m+4的最小值;(2)、求代数式24﹣2x2+8x的最大值;(3)、某居民小区要在一块靠墙(墙长15m)的空地上建一个长方形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),请问:当x取何值时,花园的面积最大?最大面积是多少? 11. 阅读材料:
11. 阅读材料:对于两个正数a、b,则 (当且仅当a=b时取等号).
当 为定值时, 有最小值;当 为定值时, 有最大值.
例如:已知 ,若 ,求 的最小值.
解:由 ≥ ,得 ≥ ,当且仅当 即 时, 有最小值,最小值为 .
根据上面的阅读材料回答下列问题:
(1)、已知 ,若 ,则当 时, 有最小值,最小值为;(2)、已知 ,若 ,则 取何值时, 有最小值,最小值是多少?(3)、用长为 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?12. 阅读理解:德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿”.(1)、如图,点把线段分成两部分,如果 , 那么称点为线段的黄金分割点.在图中,若 , 则__________(保留根号). (2)、宽与长的比是(约为)的矩形叫做黄金矩形,黄金矩形给我们以协调.匀称的美感,世界各国许多著名的建筑为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为的矩形纸片折叠黄金矩形.(提示:)
(2)、宽与长的比是(约为)的矩形叫做黄金矩形,黄金矩形给我们以协调.匀称的美感,世界各国许多著名的建筑为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为的矩形纸片折叠黄金矩形.(提示:)第一步 在矩形纸片一端,利用图的方法折出一个正方形,然后把纸片展平.
第二步 如图 , 把这个正方形折成两个相等的矩形,再把纸片展平.
第三步 如图 , 折出内侧矩形的对角线 , 并把折到图中所示的处.
第四步 展平纸片,按所得的点折出 , 使 , 则图④中就出现黄金矩形.
问题解决:

①图中(保留根号);
②请写出图中所有的黄金矩形: , 并证明;
③请结合图 , 在矩形中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并证明.
13.
【材料阅读】
我们曾解决过课本中的这样一道题目:
如图1,四边形ABCD是正方形,E为BC边上一点,延长BA至F,使AF=CE,连接DE,DF.……
提炼1:△ECD绕点D顺时针旋转90°得到△FAD;
提炼2:△ECD≌△FAD;
提炼3:旋转、平移、轴对称是图形全等变换的三种方式.
【问题解决】
(1)、如图2,四边形ABCD是正方形,E为BC边上一点,连接DE,将△CDE沿DE折叠,点C落在G处,EG交AB于点F,连接DF.可得:∠EDF=°;AF,FE,EC三者间的数量关系是 .
(2)、如图3,四边形ABCD的面积为8,AB=AD,∠DAB=∠BCD=90°,连接AC.求AC的长度.(3)、如图4,在△ABC中,∠ACB=90°,CA=CB,点D,E在边AB上,∠DCE=45°.写出AD,DE,EB间的数量关系,并证明.14. 阅读下面材料:
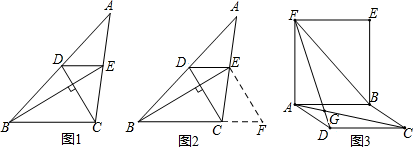
小明遇到这样一个问题:如图①,在中, , 且 , 试求的值.
(1)、小明发现,过点E作 , 交的延长线于点F , 经过推理得到 , 再计算就能够使问题得到(1)解决(如图②),并写出推理和计算过程.(2)、参考小明思考问题的方法,请你解决如下问题:如图③,已知和矩形 , 与交于点G , 求的度数.
15. 阅读下面材料,并回答下列问题:小明遇到这样一个问题,如图,在 中, 分别交 于点 ,交 于点 .已知 ,求 的值.
小明发现,过点 作 ,交 的延长线于点 ,构造 ,经过推理和计算能够使问题得到解决(如图)
请你回答:
(1)、证明: ;(2)、求出 的值;(3)、参考小明思考问题的方法,解决问题;如图,已知 和矩形 与 交于点 .求 的度数.
16. 阅读下列材料:如图1,在四边形ABCD中,若AB=AD,BC=CD,则把这样的四边形称之为筝形.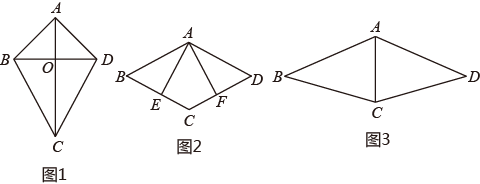 (1)、如图2,在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.(2)、如图3,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.17. 【阅读材料】如图①,在边长为4的正方形ABCD中,点E、F分别在边BC、CD上且∠EAF=45°,连接EF,求△CEF的周长.
(1)、如图2,在平行四边形ABCD中,点E、F分别在BC、CD上,且AE=AF,∠AEC=∠AFC.求证:四边形AECF是筝形.(2)、如图3,在筝形ABCD中,AB=AD=26,BC=DC=25,AC=17,求筝形ABCD的面积.17. 【阅读材料】如图①,在边长为4的正方形ABCD中,点E、F分别在边BC、CD上且∠EAF=45°,连接EF,求△CEF的周长.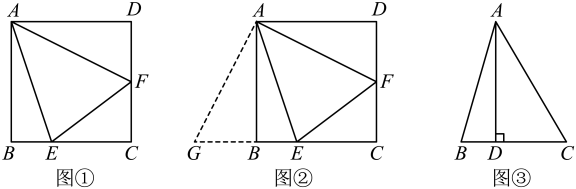
小明想到解决问题的方法如下:
如图②,延长CB至点G,使BG=DF,通过证明 , 得到BE、DF、EF之间的关系,进而求出△CEF的周长.
(1)、请按照小明的思路,帮助小明写出完整的求解过程.(2)、【方法应用】如图②,若BE=1,求DF的长.(3)、【能力提升】如图③,在锐角△ABC中,∠BAC=45°,AD⊥BC于点D.若BD=1,AD=4,则CD的长为 .18. 请阅读下列材料,并完成相应任务.勾股定理的证明
勾股定理揭示了直角三角形三条边之间的数量关系,是数学中最重要的定理之一. 勾股定理的证明过程多数采用的方法是“用两种不同的方法和含有a,b,c的式子表示同一个图形的面积”,由于同一个图形的面积相等,从而得到含a,b,c的恒等式,通过化简即可完成勾股定理的证明.借助于图形的面积研究相关的数量关系,是我国古代数学研究中经常采用的重要方法,它充分显示了古人的卓越智慧.
下面是证明勾股定理的一种思路:
如图,用一个等腰直角三角形(),和两个全等的直角三角形()可以拼成一个直角梯形 . 其中; , 用两种不同的方法和含有a,b,c的式子表示梯形的面积,就能完成勾股定理的证明.
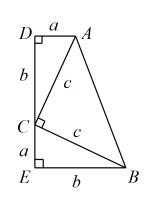
提示:梯形的面积(上底+下底)高
任务:
(1)、请你根据上述材料中的思路证明勾股定理;(2)、如图,在菱形中,对角线相交于点O, , 则之间的距离为 .