命题新趋势7 阅读理解——浙教版数学七（下）期末复习-在线组卷题库

1. 先阅读材料，然后解方程组．

材料：解方程组： $\{\begin{matrix} x + y - 2 = 0 ① \\ 3 (x + y) - y = 4 ② \end{matrix}$ ，

由①，得 $x + y = 2$ ． ③

把③代入②，得 $3 \times 2 - y = 4$ ，解得 $y = 2$ ．

把 $y = 2$ 代入③，得 $x = 0$ ．

$∴$ 原方程组的解为 $\{\begin{array}{l} x = 0 \\ y = 2 \end{array}$ ；

这种方法称为“整体代入法”，你若留心观察，有很多方程组可采用此方法解答，请用这种方法解方程组： $\{\begin{matrix} 3 x - 2 y - 1 = 0 ① \\ \frac{3 x - 2 y + 5}{6} + y = 2 ② \end{matrix}$ ．

查看试题解析

2. 阅读材料“轮换式方程组的解法”，然后解题.

材料：解方程组 ${\begin{cases} 2001 x + 2003 y = 6005 ① \\ 2003 x + 2001 y = 6007 ② \end{cases}$ 解方程组 ${\begin{cases} 2 a + 3 b = 12 ① \\ 3 a + 2 b = 13 ② \end{cases}$

解：将①+②，得 $4004 (x + y) = 12012$ ，即 $x + y = 3$ ③ 解：

将②-①，得 $2 (x - y) = 2$ ，即 $x - y = 1$ ④

将③+④，得 $2 x = 4$ ，即 $x = 2$

将 $x = 2$ 代入③，得 $2 + y = 3$ ，即 $y = 1$

所以原方程组的解为 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$

查看试题解析

3. 阅读下列材料，解决相应问题．

(1)、【学科融合】如图1，物理学光的反射现象中，把经过入射点

O

并垂直于反射面的直线

O N

叫做法线，入射光线与法线的夹角

i

叫做入射角，反射光线与法线的夹角

r

叫做反射角，反射角

r =

入射角

i

，这就是光的反射定律．

在图1中，证明 $∠ 1 = ∠ 2$ ；

(2)、【问题解决】根据光的反射定律，人们制造了潜望镜，如图2是潜望镜的工作原理示意图，

A B

、

C D

是平行放置的两面平面镜，

E F

是射入潜望镜的光线，

G H

是经平面镜两次反射后离开潜望镜的光线，由可知，光线经过平面镜反射时，有

∠ 2 = ∠ 1

，

∠ 4 = ∠ 5

；

①请问 $∠ 2$ 和 $∠ 5$ 有什么关系？并说明理由；

②请问光线 $E F$ 和 $G H$ 是否平行？并说明理由．

查看试题解析

4. 阅读下面的材料：

材料一：比较 $3^{22}$ 和 $4^{11}$ 的大小．	材料二：比较 $2^{8}$ 和 $8^{2}$ 的大小．
解：因为 $4^{11} = {(2^{2})}^{11} = 2^{22}$ ，且 $3 > 2$ ，所以 $3^{22} > 2^{22}$ ，即 $3^{22} > 4^{11}$ ．	解：因为 $8^{2} = {(2^{3})}^{2} = 2^{6}$ ，且 $8 > 6$ ，所以 $2^{8} > 2^{6}$ ，即 $2^{8} > 8^{2}$ ．
小结：指数相同的情况下，通过比较底数的大小，来确定两个幂的大小．	小结：底数相同的情况下，通过比较指数的大小，来确定两个幂的大小．

解决下列问题：

(1)、比较

3^{44}

，

4^{33}

，

5^{22}

的大小；

(2)、比较

8 1^{31}

，

2 7^{41}

，

9^{61}

的大小．

查看试题解析

5. 请阅读下列材料：我们规定一种运算：

[a, b] = 2 a - b

，比如：

[3, - 1] = 2 \times 3 - (- 1) = 7

．

按照这种规定的运算，请解答下列问题：

(1)、填空：计算

[- 5, - 6] =

；

(2)、若

[x, - y] = 2, [1 - x, 2 y] = - 6

，且满足

1 \leq [k x, 1 + y] \leq 5

，请你求出k的整数值．

查看试题解析

6. 【阅读理解】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到

{(a + b)}^{2} = a^{2} + 2 a b + b^{2}

，基于此，请解答下列问题：

(1)、【类比应用】①若

x y = 8

，

x + y = 6

，则

x^{2} + y^{2}

的值为；

②若 $x (5 - x) = 6$ ，则 $x^{2} + {(5 - x)}^{2} =$ ；

(2)、【迁移应用】两块完全相同的特制直角三角板

(∠ A O B = ∠ C O D = 90 °)

如图2所示放置，其中

A

，

O

，

D

在一直线上，连接

A C

，

B D

，若

A D = 14

，

S_{Δ A O C} + S_{Δ B O D} = 54

，求一块三角板的面积．

查看试题解析

7. 阅读材料，并解答下列问题：

我们知道，利用图形面积的不同计算方法，有些几何图形能直观地反应某些恒等式的对应关系．

例如：

(1)、如图1，反应的是a²+2ab+b²= ．

(2)、如图2，反应的是a²-b²= ．

(3)、如图3，反应的是2a²+3ab+b²= ．

查看试题解析

8. 阅读理解：

符号 $|\begin{matrix} a & c \\ b & d \end{matrix}| ，$ 称为二阶行列式，规定它的运算法则为 $|\begin{matrix} a & c \\ b & d \end{matrix}| = a d - b c .$ 例如 $|\begin{matrix} 3 & 5 \\ 2 & 4 \end{matrix}| = 3$ ×4-2×5=2.

请根据以上材料，化简下面的二阶行列式：

$|\begin{matrix} \frac{a}{a - 1} & a + 1 \\ \frac{1}{1 - a} & 1 \end{matrix}| .$

查看试题解析

9. 阅读材料：

已知实数x满足 $x^{2} = 2 x + 1 ，$ 则

$x^{3} = x \cdot x^{2} = x (2 x + 1)$

$= 2 x^{2} + x$

=2(2x+1)+x=5x+2.

解决问题：

已知实数x满足 $x^{2} - 3 x + 1 = 0 ，$ 求x³-8x的值.

查看试题解析

10. 【阅读理解】阅读下列解方程组的方法，然后解决问题．

解方程组 ${\begin{array}{l} 16 x + 14 y = 170 ① \\ 14 x + 16 y = 130 ② \end{array}$ 时，如果直接考虑消元，那么非常麻烦，而采用下列解法则轻而易举．

解：①＋②， $30 x + 30 y = 300$ ，

即 $x + y = 10$ ③

①－②， $2 x - 2 y = 40$

即 $x - y = 20$

联立③和④，得 ${\begin{array}{l} x + y = 10 ① \\ x - y = 20 ② \end{array}$

解得 ${\begin{array}{l} x = 15 \\ y = - 5 \end{array}$

所以原方程组的解为 ${\begin{array}{l} x = 15 \\ y = - 5 \end{array}$

(1)、由二元一次方程组

{\begin{array}{l} 2 x + 3 y = 6 \\ 3 x + 2 y = 4 \end{array}

，可得

x + y =

；

x - y =

．

(2)、解方程组

{\begin{array}{l} 2024 x + 2025 y = 2023 \\ 2022 x + 2023 y = 2021 \end{array}

(3)、【拓展提升】

对于实数x ， y ，定义新运算： $x * y = a x + b y + c$ ，其中a ， b ， c是常数，例如： $5 * 6 = 5 a + 6 b + c$ ．

已知 $2 * 4 = 15 ， 3 * 7 = 27$ ，则 $1 * 1 =$ ．

查看试题解析

11. 【阅读思考】如图①，已知

A B ∥ E D

，探究

∠ B

、

∠ E

、

∠ B C E

之间关系，小明添加了一条辅助线．解决了这道题．得到的结果是

∠ B + ∠ E = ∠ B C E

．

证明过程如下：

如图①，过点 $C$ 作 $C F ∥ A B$

$∴ ∠ B = ∠ 1$ ．

$∵ A B ∥ E D, A B ∥ C F$ ，

$∴ D E ∥ C F$ ，

$∴ ∠ E = ∠ 2$ ，

$∴ ∠ B + ∠ E = ∠ 1 + ∠ 2$ ，即 $∠ B + ∠ E = ∠ B C E$ ．

(1)、【理解应用】如图②，已知

A B ∥ E D

，求

∠ B + ∠ B C D + ∠ D

的度数；

(2)、【拓展探索】如图③，已知

A B ∥ C D

，点

C

在点

D

的右侧，

∠ A D C = 50 °

，

B E

平分

∠ A B C

，

D E

平分

∠ A D C

，

B E

，

D E

所在的直线交于点

E

，点

E

在直线

A B

与

C D

之间，点

B

在点

A

的右侧，且

A B < C D

，

A D < B C

，若

∠ A B C = n °

，则

∠ B E D

度数为？（用含

n

的代数式表示）

查看试题解析

12. 阅读材料：

因为 $x^{2} + 2 x - 3 = (x + 3) (x - 1) ，$ ，这说明多项式 $x^{2} + 2 x - 3$ 有一个因式为x $-$ 1，我们把x=1代入此多项式发现 x=1能使多项式 $x^{2} + 2 x - 3$ 的值为0.

解决问题：

(1)、若x

-

3是多项式

x^{2} + k x + 12

的一个因式，求 k 的值.

(2)、x-3和x-4时多项式x³+mx²+12x+n的两个因式，试求m、n的值.

(3)、在(2)的条件下，把多项式

x^{3} + m x^{2} + 12 x + n

分解因式.

查看试题解析

13. 阅读理解：

若x满足 $(210 - x) (x - 200) = - 204$ ，试求 ${(210 - x)}^{2} + {(x - 200)}^{2}$ 的值，

解：设 $(210 - x) = a$ ， $(x - 200) = b$ ，则 $a b = - 204$ ，且a＋b＝(210－x)＋(x－200)＝10，

∵ ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，

∴ $a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 1 0^{2} - 2 \times (- 204) = 508$ ，即 ${(210 - x)}^{2} + {(x - 200)}^{2}$ 的值为 $508$ ．

解决问题

(1)、若x满足

(2022 - x) (x - 2010) = 22

，则

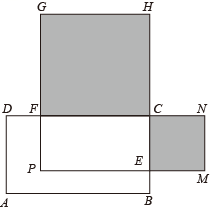{(2022 - x)}^{2} + {(x - 2010)}^{2} =

；

(2)、若(2022－x)²＋(x－2002)²＝2020，求

(2022 - x) (x - 2002)

的值；

(3)、如图，在长方形ABCD中，AB＝10，BC＝6，点E ， F分别是BC ， CD上的点，且BE＝DF＝x ，分别以FC ， CE为边在长方形ABCD外侧作正方形CFGH 和CEMN ，若长方形CEPF的面积为40平方单位，则图中阴影部分的面积和为多少？

查看试题解析

14. 阅读探索：

小明在解方程组 ${\begin{array}{l} (a - 1) + 2 (b + 2) = 2 \\ 2 (a - 1) + (b + 2) = - 2 \end{array}$ 时发现若设 $a - 1 = x$ ， $b + 2 = y$ ，

则方程组可变为 ${\begin{array}{l} x + 2 y = 2 \\ 2 x + y = - 2 \end{array}$ ，解此方程组得： ${\begin{array}{l} x = - 2 \\ y = 2 \end{array}$ ，

即 ${\begin{array}{l} a - 1 = - 2 \\ b + 2 = 2 \end{array}$ ，所以 ${\begin{array}{l} a = - 1 \\ b = 0 \end{array}$ ．

(1)、请你模仿运用上述方法解下列方程组

{\begin{array}{l} (\frac{a}{3} - 1) + 2 (\frac{b}{5} + 2) = 4 \\ 2 (\frac{a}{3} - 1) + (\frac{b}{5} + 2) = 5 \end{array}

(2)、若已知关于x、y的方程组

{\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}

的解是

{\begin{array}{l} x = 3 \\ y = 4 \end{array}

，请直接写出关于m、n的方程组

{\begin{array}{l} 5 a_{1} (m + 3) + 3 b_{1} (n - 2) = c_{1} \\ 5 a_{2} (m + 3) + 3 b_{2} (n - 2) = c_{2} \end{array}

的解．

查看试题解析

15. 阅读材料：

整体代换是一个重要的数学思想，有着广泛的应用.例如：计算4(a+b)-7(a+b)+(a+b)时可将(a+b)看成一个整体，合并同类项得-2(a+b)，再利用分配律去括号得-2a-2b.同时，我们也知道，代数的基本要义就是用字母表示数，使之更具一般性.所以，在计算a(a+b)时，同样可以利用分配律得 $a^{2} + a b$

解决问题：

(1)、请你尝试着把(a-2)或(b-2)看成整体，计算：(a-2)(b-2).

(2)、如果两个数的乘积等于它们的和的两倍，那么我们称这两个数为“积倍和数对”，即：若ab=2(a+b)，则a，b是一对“积倍和数对”，记为(a，b).例如：∵3×6=2(3+6)，∴3和6是一对“积倍和数对”，记为(3，6).

请你找出所有的a，b均为整数的“积倍和数对”

查看试题解析

16. 阅读下列解方程组的方法，然后解答问题：

解方程组 ${\begin{array}{l} 14 x + 15 y = 16 ① \\ 17 x + 18 y = 19 ② \end{array}$ 时，由于x、y的系数及常数项的数值较大，如果用常规的代入消元法、加减消元法来解，那将是计算量大，且易出现运算错误，而采用下面的解法则比较简单：

②-①得： $3 x + 3 y = 3$ ，所以 $x + y = 1$ ③

③×14得： $14 x + 14 y = 14$ ④

①-④得： $y = 2$ ，从而得 $x = - 1$

所以原方程组的解是 ${\begin{array}{l} x = - 1 ① \\ y = 2 ② \end{array}$

(1)、请你运用上述方法解方程组

{\begin{array}{l} 2022 x + 2023 y = 2024 \\ 2025 x + 2026 y = 2027 \end{array}

(2)、请你直接写出方程组

{\begin{array}{l} 2077 x - 2078 y = 2079 \\ 2078 x - 2079 y = 2080 \end{array}

的解是；

(3)、猜测关于x、y的方程组

{\begin{array}{l} m x + (m + 1) y = m + 2 \\ n x + (n + 1) y = n + 2 \end{array} (m \neq n)

的解是什么？并用方程组的解加以验证．

查看试题解析

17. 【阅读材料】我们知道，图形也是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，而运用代数思想也能巧妙地解决些图形问题.

在一次数学活动课上，张老师准备了若干张如图1所示的甲、乙、丙三种纸片，其中甲种纸片是边长为x的正方形，乙种纸片是边长为y的正方形，丙种纸片是长为y ，宽为x的长方形.并用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成了如图2所示的一个大正方形.

(1)、【理解应用】

观察图2，用两种不同方式表示阴影部分的面积可得到一个等式，请你直接写出这个等式.

(2)、【拓展升华】

利用（1）中的等式解决下列问题.

①已知 $a^{2} + b^{2} = 10$ ， $a + b = 6$ ，求 $a b$ 的值；

②已知 $(2021 - c) (c - 2019) = - 2020$ ，求 ${(2021 - c)}^{2} + {(c - 2019)}^{2}$ 的值.

查看试题解析

18. 阅读材料，回答下列问题：

要比较a与b的大小，可先求出a与b的差，再看这个差是正数、负数还是零．由此可见，要判断两个代数式值的大小，只要考虑它们的差就可以了．已知甲、乙两人两次同时在同一粮店购买粮食(假设两次购买粮食的单价不相同)，甲每次购买粮食100kg，乙每次购买粮食用去100元

(1)、假设x，y分别表示两次买粮食的单价(单价：元/kg)．

①试用含x，y的代数式表示：甲两次购买粮食共需付款元．

②乙两次共购买kg的粮食．

③若甲两次购粮的平均单价为每千克Q₁元，乙两次购粮的平均单价为每千克Q₂元，则Q1= ， Q₂=

(2)、规定：谁两次购粮的平均单价低，谁的购粮方式就更合算．请你判断甲、乙两人的购粮方式中哪一个更合算．并说明理由．

查看试题解析

19. 阅读下面的材料：

$\frac{1}{2} \times \frac{3}{2} = (1 - \frac{1}{2}) (1 + \frac{1}{2}) = 1 - \frac{1}{2^{2}}$ ；

$\frac{2}{3} \times \frac{4}{3} = (1 - \frac{1}{3}) (1 + \frac{1}{3}) = 1 - \frac{1}{3^{2}}$ ；

……

利用上面材料中的方法解答下列各题：

(1)、①

\frac{3}{4} \times \frac{5}{4} = (1 - \frac{1}{4}) (1 + \frac{1}{4}) = 1 -

；

② $\frac{6}{7} \times \frac{8}{7} =$ $= 1 -$ ；

(2)、计算：

(1 - \frac{1}{5}) \times (1 + \frac{1}{5}) \times (1 + \frac{1}{5^{2}}) \times (1 + \frac{1}{5^{4}}) + \frac{1}{5^{8}}

．

查看试题解析

命题新趋势7 阅读理解——浙教版数学七（下）期末复习

一、实践探究题