命题新趋势6 开放型问题——2024年北师大版数学七(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 现有2cm,3cm,5cm,6cm长的四根木棒,任选其中的三根组成三角形,那么可以组成三角形的个数有( )A、1个 B、2个 C、3个 D、4个2.
一块三角形玻璃样板不慎被小强同学碰破,成了四片完整四碎片(如图所示),聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板.你认为下列四个答案中考虑最全面的是( )
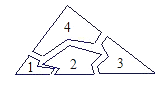 A、带其中的任意两块去都可以 B、带1、2或2、3去就可以了 C、带1、4或3、4去就可以了 D、带1、4或2、4或3、4去均可3. 如图,和相交于点E, , 请添加一个条件(只添加一个即可),使 , 下列不正确的是( )
A、带其中的任意两块去都可以 B、带1、2或2、3去就可以了 C、带1、4或3、4去就可以了 D、带1、4或2、4或3、4去均可3. 如图,和相交于点E, , 请添加一个条件(只添加一个即可),使 , 下列不正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
4. 如图, , , 三点在同一条直线上,在不添加辅助线的情况下,请你添加一个条件 , 使(填一个即可).
 5. 如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件: . (只写一个即可,不添加任何字母或数字)
5. 如图,点B、C、E在同一条直线上,请你写出一个能使成立的条件: . (只写一个即可,不添加任何字母或数字)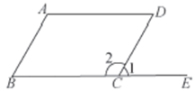 6. 如图,直线 , 被直线所截,若要证明直线 , 需要添加条件 . (填一个条件即可)
6. 如图,直线 , 被直线所截,若要证明直线 , 需要添加条件 . (填一个条件即可) 7. 如图, , 现要添加一个条件使 , 可以添加 . (只添一个即可).
7. 如图, , 现要添加一个条件使 , 可以添加 . (只添一个即可). 8. 如图,已知四边形 , 要使 , 添加的条件是 填一个即可 .
8. 如图,已知四边形 , 要使 , 添加的条件是 填一个即可 .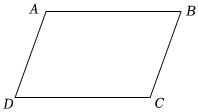 9. 如图,请写出一个能使得DE∥BC的条件:.(只写一个即可)
9. 如图,请写出一个能使得DE∥BC的条件:.(只写一个即可)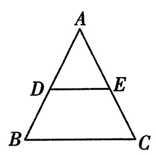 10. ① , ② , ③ , ④ , ⑤ , 任选两个作为题设,一个作为结论,构成一个真命题.你的选择是:题设是 , 结论是 . (填写编号)
10. ① , ② , ③ , ④ , ⑤ , 任选两个作为题设,一个作为结论,构成一个真命题.你的选择是:题设是 , 结论是 . (填写编号) 11. 如图,点O在直线上,过点O作射线 , , . 从下面的四个条件中任选两个,可以推出的是(写出一组满足题意的序号).
11. 如图,点O在直线上,过点O作射线 , , . 从下面的四个条件中任选两个,可以推出的是(写出一组满足题意的序号).①;②和互余;③;④ .
 12. 如图,在三角形纸片ABC中,∠ACB=90°,∠A=40°,点D在AB边上(不与A、B重合),连接CD,将△ACD沿CD所在直线折叠得到△A′CD,A′C交AB于点E.
12. 如图,在三角形纸片ABC中,∠ACB=90°,∠A=40°,点D在AB边上(不与A、B重合),连接CD,将△ACD沿CD所在直线折叠得到△A′CD,A′C交AB于点E.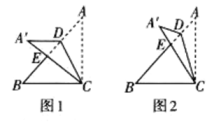
请从A、B两题中任选一题作答.我选择题.
A.如图1,若A′D∥BC,则∠ACD的度数为 .
B.如图2,若A′E=A′D,则∠ACD的度数为 .
13. 已知某三角形的两条边长分别为4和9,则其第3三边的长可能是 . (写出一个即可)14. 如图,点C在射线上,只需添加一个条件即可证明 , 这个条件可以是(写出一个即可). 15. 如图, , 在不添加其他辅助线的情况下,若要使直线 , 则需要添加的条件为(写出一个即可).
15. 如图, , 在不添加其他辅助线的情况下,若要使直线 , 则需要添加的条件为(写出一个即可). 16. 如图,点A,B,C,D在同一条直线上,若满足条件 , 则有CE∥DF,理由是 . (要求:不再添加辅助线,只需填一个答案即可)
16. 如图,点A,B,C,D在同一条直线上,若满足条件 , 则有CE∥DF,理由是 . (要求:不再添加辅助线,只需填一个答案即可) 17. 如图,在和中,点B , F , C , E在同一直线上, , , 请添加一个条件,使得 . 添加的条件可以是(只需写一个,不添加辅助线);
17. 如图,在和中,点B , F , C , E在同一直线上, , , 请添加一个条件,使得 . 添加的条件可以是(只需写一个,不添加辅助线);
三、作图题
-
18. 在的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形,画出符合条件的小正方形(最少两种).
 19. 如图,点A、C在∠MON的一边OM上,AB⊥ON于点B,CD⊥OM交射线ON于点D.按要求画图并猜想证明:
19. 如图,点A、C在∠MON的一边OM上,AB⊥ON于点B,CD⊥OM交射线ON于点D.按要求画图并猜想证明: (1)、过点C画ON的垂线段CE,垂足为点E;(2)、过点E画EF∥OC,交CD于点F.请你猜想∠OAB与∠CEF的数量关系,并证明你的结论.
(1)、过点C画ON的垂线段CE,垂足为点E;(2)、过点E画EF∥OC,交CD于点F.请你猜想∠OAB与∠CEF的数量关系,并证明你的结论.四、解答题
-
20. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.
 21. 如图, , 分别探讨下面四个图形中与、的关系,请你从(3)或(4)中任选一个加以说明.
21. 如图, , 分别探讨下面四个图形中与、的关系,请你从(3)或(4)中任选一个加以说明. 22. 如图,在中,线段是的高.给出下列三个选项:①;②;③ . 从上述三个选项中任选两个作为条件,另一个作为结论,使结论成立,并说明理由.
22. 如图,在中,线段是的高.给出下列三个选项:①;②;③ . 从上述三个选项中任选两个作为条件,另一个作为结论,使结论成立,并说明理由.
已知: ▲ , 结论: ▲ . (填序号)
理由:
23. 如图,有三个论断:①;②;③ , 请你从中任选两个作为条件,另一个作为结论构成一个命题,并证明该命题的正确性.已知: ▲ . 结论: ▲ .
理由:
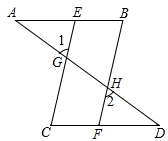 24. 如图, , 点是直线之间的一点,连接 .
24. 如图, , 点是直线之间的一点,连接 .探究猜想:
①若 , 则 ▲ ;
②若 , 则 ▲ ;
③猜想图中的关系,并证明你的结论.
 25. 如图,已知点是线段上一点, , . 猜想、、之间的数量关系并证明.
25. 如图,已知点是线段上一点, , . 猜想、、之间的数量关系并证明. 26. 如图,有三个条件:① , ② , ③ , 从中任选两个作为已知条件,另一个作为结论,可以组成3个命题,例如:
26. 如图,有三个条件:① , ② , ③ , 从中任选两个作为已知条件,另一个作为结论,可以组成3个命题,例如:以③作为结论的命题是:如图,已知 , , 求证:
 (1)、请按要求写出命题:
(1)、请按要求写出命题:以①作为结论的命题是:;
以②作为结论的命题是:;
(2)、请证明以②作为结论的命题.27. 【问题呈现】小明在学习中遇到这样一个问题:如图①,在中, , 平分、于D , 猜想、、的数量关系. (1)、小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入、的特殊值求值并寻找它们的数量关系,得到下面几组对应值:(单位:度)
(1)、小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入、的特殊值求值并寻找它们的数量关系,得到下面几组对应值:(单位:度)10
30
30
20
20
70
70
60
60
80
30
a
15
20
30
上表中a= , 猜想与、的数量关系并证明 .
(2)、【变式应用】小明继续研究,在图②中, , , 其它条件不变,若把“于D”改为“点F是线段上任意一点,于D”,则(直接写出结果).
(3)、小明提出问题,在中, , 平分 , 若点F是线段延长线上一点,于D , 试探究与、的数量关系(直接写出结论,不需证明).