命题新趋势6 开放型问题——2024年浙教版数学八（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 一场有19位同学参加的比赛，取前10名进决赛且所得分数互不相同.某同学知道自己的分数后要判断是否能进决赛，他只需要知道这19位同学所得分数的（）

A、平均数 B、中位数 C、众数 D、方差

查看试题解析
2. 已知四边形ABCD的对角线AC、BD相交于点O，给出下列5个条件：①AB∥CD；②OA＝OC；③AB＝CD；④∠BAD＝∠DCB；⑤AD∥BC，从以上5个条件中任选2个条件为一组，能判定四边形ABCD是平行四边形的有（）组.

A、4 B、5 C、6 D、7

查看试题解析
3. 如图，在▱ABCD中，点E在边AD上，过E作EF $∥$ CD交对角线AC于点F ，若要求△FBC的面积，只需知道下列哪个三角形的面积即可（）

A、△ECD B、△EBF C、△EBC D、△EFC

查看试题解析
4. 如图所示，一个大矩形被分成4个大小不同的正方形①、②、③、④和一个矩形⑤，若要计算该矩形⑤的周长，则只需要知道哪一个小正方形的周长？你的聪明选择是（）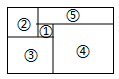

A、① B、② C、③ D、④

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ，分别以AB、AC为边向外作正方形ABDE和AFGC.若想要求出 $△ A C D$ 的面积，则只需知道以下哪个图形的面积（）

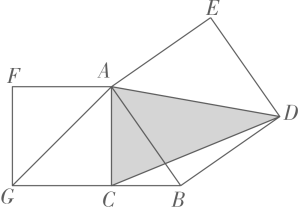A、 $△ A B C$ B、 $△ A B G$ C、正方形ABDE D、四边形AFGB

查看试题解析
6. 四边形ABCD和CEFG都是正方形， $E$ 在CD上，连结AF交对角线BD于点 $H$ ，交DE于点 $I$ .若要求两正方形的面积之和，则只需知道（）

A、IF的长 B、BH的长 C、AH的长 D、CI的长

查看试题解析
7. 如图， $R t △ A B C$ 中∠ACB是直角，分别以 $△ A B C$ 的三边向外作正方形，G为 $△ C E F$ 边EF的中点，若要求出图中阴影 $△ B D G$ 的面积，只需要知道线段（）

A、AB的长度 B、AC的长度 C、BC的长度 D、BG的长度

查看试题解析
8. 如图，正方形AMNP和正方形EFGH是两个全等的正方形，将它们按如图的方式放置在正方形ABCD内，若求阴影图形的面积，则只需知道（）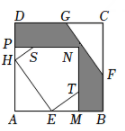

A、△AHE的面积 B、五边形HETNS的面积 C、△EMT的面积 D、正方形AMNP的面积

查看试题解析
9. 如图， $▱ E F G H$ 的四个顶点分别在 $▱ A B C D$ 的四条边上， $Q F ∥ A D$ ，分别交EH、CD于点P、Q过点P作 $M N ∥ A B$ ，分别交AD、BC于点M、N，若要求 $▱ E F G H$ 的面积，只需知道下列哪个四边形的面积（）

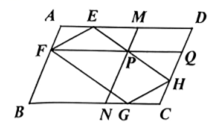A、四边形AFPM B、四边形MPQD C、四边形FBNP D、四边形PNCQ

查看试题解析
10. 如图，正方形 $A B C D$ 的边 $A B$ ， $C D$ 上各有一个点 $I$ ， $E$ ，连结 $E I$ ，且 $E I // B C$ ，点 $F$ ， $G$ ， $H$ 分别在 $A D$ ， $A B$ ， $B C$ 边上，连结 $G F$ ， $F E$ ， $E H$ ， $H G$ ，其中 $E I$ 与 $G F$ 相交于点 $J$ ， $I J = A I$ ，为求出平行四边形 $E F G H$ 的面积，只需知道下列哪条边的长度（）

A、 $I G$ B、 $A F$ C、 $B G$ D、 $A G$

查看试题解析

二、填空题

11. 在四边形ABCD中，AD∥BC，∠D=90°，要使它变成矩形，需要添加的一个条件是(写出一种情况即可).

查看试题解析
12. 要使 $▱ A B C D$ 成为矩形，需增加的一个条件是.（只需写出一种情况）

查看试题解析
13. 构造一个一元二次方程，要求：①常数项不为0；②有一个根为-1.这个一元二次方程可以是(写出一个即可).

查看试题解析
14. 对甲、乙两位同学近六次数学测试成绩进行统计分析，已知甲测试成绩的方差是 $2.3$ ，甲的成绩比乙的成绩更稳定，则乙测试成绩的方差可能是（写出一个即可）．

查看试题解析
15. 我们已经学习了一元二次方程的多种解法：如因式分解法，开平方法，配方法和公式法，还可以运用十字相乘法，请从以下一元二次方程中任选一个，并选择你认为适当的方法解这个方程．
①x²﹣4x﹣1=0
②x（2x+1）=8x﹣3
③x²+3x+1=0
④x²﹣9=4（x﹣3）
我选择第个方程．

查看试题解析
16. 如图，在▱ABCD中，点F，E分别在边AD，BC上，若要使AE=CF，则需添加的条件是(填一个即可).

查看试题解析
17. 在四边形ABCD中，已知AB∥CD，AD∥BC，添加一个条件，即可判定该四边形是菱形.

查看试题解析
18. 已知一个一元二次方程的一个根为2023，二次项系数是1，则这个一元二次方程可以是(只需写出一个方程即可)．

查看试题解析

三、解答题

19. 解方程：我们已经学习了一元二次方程的多种解法：如因式分解法，开平方法，配方法和公式法，还可以运用十字相乘法，请从以下一元二次方程中任选两个，并选择你认为适当的方法解这个方程
① $x^{2} - 4 x- 1 = 0$ ② $x (2 x + 1) = 8 x - 3$
③ $x^{2} + 3 x + 1 = 0$ ④ $x^{2} - 9 = 4 (x - 3)$

查看试题解析
20.
学了一元二次方程后，学生小刚和小明都想出个问题考考对方．下面是他们俩的一段对话：聪明的你能替小刚或小明解决问题吗？（要求任选一人回答）

查看试题解析
21.
如图，四边形ABCD中，AB=CD，点E、F、G、H分别是BC、AD、BD、AC的中点，猜想四边形EHFG的形状并说明理由．

查看试题解析
22. 探索规律
先观察下列各式，再回答问题． $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}}$ =1 $\frac{1}{2}$ ； $\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}}$ =1 $\frac{1}{6}$ ； $\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}}$ =1 $\frac{1}{12}$ ．
（1）根据上面三个等式提供的消息，请猜想 $\sqrt{1 + \frac{1}{4^{2}} + \frac{1}{5^{2}}}$ 的结果，不用验证；
（2）按照上面各等式反映的规律，试写出用含n的式子表示的等式（n为正整数），不用验证．

查看试题解析
23. 观察下列各式及其验证过程：
$2 \sqrt{\frac{2}{3}}$ = $\sqrt{2 + \frac{2}{3}}$
验证： $2 \sqrt{\frac{2}{3}}$ = $\sqrt{\frac{2^{3}}{3}}$ = $\sqrt{\frac{(2^{3} - 2) + 2}{2^{2} - 1}}$ = $\sqrt{\frac{2 (2^{2} - 1) + 2}{2^{2} - 1}}$ = $\sqrt{2 + \frac{2}{3}}$ $\cdot 3 \sqrt{\frac{3}{8}}$ = $\sqrt{3 + \frac{3}{8}}$
验证： $3 \sqrt{\frac{3}{8}}$ = $\sqrt{\frac{3^{3}}{8}}$ = $\sqrt{\frac{(3^{3} 3) + 3}{3^{2} 1}}$ = $\sqrt{\frac{3 (3^{2} 1) + 3}{3^{2} 1}}$ = $\sqrt{3 + \frac{3}{8}}$
（1）按照上述两个等式及其验证过程的基本思路，猜想 $5 \sqrt{\frac{5}{24}}$ 的变形结果并进行验证；
（2）针对上述各式反应的规律，写出用n（n为任意自然数，且n≥2）表示的等式，并说明它成立．

查看试题解析