命题新趋势5 新定义——2024年北师大版数学八（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 定义一种运算： $a # b = b - a (a \geq b)$ ，现有两个满足该运算条件的式子： $a = 2 x - 1$ 和 $b = 1 - x$ ，则不等式 $(2 x - 1) # (1 - x) > - 1$ 的解集是（）

A、 $\frac{2}{3} \leq x < 1$ B、 $x < 1$ C、 $x > 1$ D、 $x \geq \frac{2}{3}$

查看试题解析
2. 定义一种新运算：当 $a > b$ 时， $a * b = a b + b$ ；当 $a < b$ 时， $a * b = a b - b$ ．若 $3 * (x + 2) > 0$ ，则x的取值范围是（）

A、 $- 1 < x < 1$ 或 $x < - 2$ B、 $x < - 2$ 或 $1 < x < 2$ C、 $- 2 < x < 1$ 或 $x > 1$ D、 $x < - 2$ 或 $x > 2$

查看试题解析
3. 对于实数 $a$ 和 $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{1}{1 - b^{2}}$ ，这里等式右边是实数运算．例如： $5 \otimes 3 = \frac{1}{1 - 3^{2}} = - \frac{1}{8}$ ．则方程 $x \otimes 2 = \frac{2}{x - 4} - 1$ 的解是（）

A、 $x = 4$ B、 $x = 5$ C、 $x = 6$ D、 $x = 7$

查看试题解析
4. 对于实数 $a$ ， $b$ ，定义一种新运算“ $\otimes$ ”为： $a \otimes b = \frac{2}{a - b^{2}}$ ，这里等式右边是通常的实数运算.例如： $1 \otimes 3 = \frac{2}{1 - 3^{2}} = - \frac{1}{4}$ ，则方程 $x \otimes (- 1) = \frac{6}{x - 1} - 1$ 的解是（）

A、 $x = 4$ B、 $x = 5$ C、 $x = 6$ D、 $x = 7$

查看试题解析
5. 对于任意实数a、b，定义一种运算：a※b＝ab﹣a+b﹣2.例如，2※5＝2×5﹣2+5﹣2＝11.请根据上述的定义解决问题：若不等式2※x＞2，则不等式的解为（　　）

A、x＞1 B、x＞2 C、x＜1 D、x＜2

查看试题解析
6. 定义：点A（x，y）为平面直角坐标系内的点，若满足x=y，则把点A叫做“平衡点”．例如：M（1，1），N（-2，-2），都是“平衡点”．当 $- 1 \leq x \leq 3$ 时，直线 $y = 2 x + m$ 上有“平衡点”，则 $m$ 的取值范围是（）．

A、 $0 \leq m \leq 1$ B、 $- 3 \leq m \leq 1$ C、 $- 3 \leq m \leq 3$ D、 $- 1 \leq m \leq 0$

查看试题解析
7. 对于实数 $a ， b$ ，定义符号 $m i n {a ， b}$ 其意义为：当 $a \geq b$ 时， $m i n {a ， b} = b$ ；当 $a < b$ 时， $m i n {a ， b} = a$ ．例如： $m i n {2 ， - 1} = - 1$ ，若关于 $x$ 的函数 $y = m i n {2 x - 1 ， - x + 3}$ ，则该函数的最大值是（）

A、1 B、 $\frac{4}{3}$ C、 $\frac{5}{3}$ D、2

查看试题解析

二、填空题

8. 定义运算“※”： $a ※ b = {\begin{array}{l} \frac{2}{a - b} (a > b) \\ \frac{2}{b - a} (a < b) \end{array}$ ，若 $3 ※ x = 1$ ，则 $x$ 的值为．

查看试题解析
9. 现定义一种新运算： $x \oplus y = {\begin{array}{l} x + y ， x \geq y \\ x - y ， x < y \end{array}$ ，若 $a$ 满足 $(3 a - 1) \oplus (2 a + 3) > - 5$ ，则 $a$ 的取值范围为．

查看试题解析
10. 我们定义一种新运算： $x \otimes y = \frac{x y}{3} - 2 y$ ，如 $2 \otimes 3 = \frac{2 \times 3}{3} - 2 \times 3 = - 4$ ，则关于a的不等式 $2 \otimes a \leq 2$ 的最小整数解为．

查看试题解析
11. 定义 $F (x ， y) = \frac{a x - b y}{x - 1}$ ，如： $F (3 ， 2) = \frac{3 a - 2 b}{3 - 1}$ ．若 $F （ 2 ， 3 ） = 1$ ， $F (3 ， 1) = \frac{5}{2}$ ，且关于x的方程 $F （ x ， k ） + F （ x + 1 ， 2 x ） = 2$ 无解，则实数k的值为．

查看试题解析
12. 如图，在平面直角坐标系 $x O y$ 中，对于点 $P (x_{1} ， y_{1})$ ，给出如下定义：当点 $Q (x_{2} ， y_{2})$ 满足 $x_{1} \cdot x_{2} = y_{1} \cdot y_{2}$ 时，称点Q是点P的等积点．已知点 $P (1 ， 2)$ ．

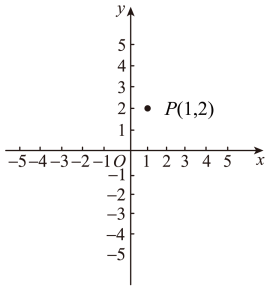(1)、在 $Q_{1} (2 ， 3)$ ， $Q_{2} (- 4 ， - 2)$ ， $Q_{3} (5 ， 3)$ 中，点P的等积点是．

(2)、点Q是点P的等积点，点C在x正半轴上，以O，P，Q，C为顶点的四边形是平行四边形，则点C的坐标为．

查看试题解析
13. 定义：如果三角形有两个内角的差为60°，那么这样的三角形叫做“准等边三角形”那么顶角为120°的等腰三角形 “准等边三角形”．（填“是”或“不是”）

查看试题解析

三、实践探究题

14. 对于实数a、b，定义一种新运算“⊗”为：a⊗b= $\frac{2}{a^{2} + a b}$ ，这里等式右边是通常的四则运算．请解方程（﹣2）⊗x=1⊗x．

查看试题解析
15. 定义：若分式 $A$ 与分式 $B$ 的差等于它们的积，即 $A - B = A B$ ，则称分式 $B$ 是分式 $A$ “友好分式”．
如 $\frac{1}{x + 1}$ 与 $\frac{1}{x + 2}$ ，因为 $\frac{1}{x + 1} - \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ， $\frac{1}{x + 1} \times \frac{1}{x + 2} = \frac{1}{(x + 1) (x + 2)}$ ，

所以 $\frac{1}{x + 2}$ 是 $\frac{1}{x + 1}$ 的“友好分式”．

(1)、分式 $\frac{2}{2 y + 5}$ $\frac{2}{2 y + 3}$ 分式的“友好分式”（填“是”或“不是”）；

(2)、小明在求分式 $\frac{1}{x^{2} + y^{2}}$ 的“友好分式”时，用了以下方法：
设 $\frac{1}{x^{2} + y^{2}}$ 的“友好分式”为 $N$ ，则 $\frac{1}{x^{2} + y^{2}} - N = \frac{1}{x^{2} + y^{2}} \times N$ ，
∴ $(\frac{1}{x^{2} + y^{2}} + 1) N = \frac{1}{x^{2} + y^{2}}$ ，
∴ $N = \frac{1}{x^{2} + y^{2} + 1}$ ．
请你仿照小明的方法求分式 $\frac{x}{x - 3}$ 的“友好分式”．

(3)、①观察（1）（2）的结果，寻找规律，直接写出分式 $\frac{b}{a x + b}$ 的“友好分式”：．
②若 $\frac{n + 2}{m x + m^{2} + n}$ 是 $\frac{m - 1}{m x + n^{2}}$ 的“友好分式”，则 $m + n$ 的值为．

查看试题解析
16. 定义：如果一元一次方程的解也是一元一次不等式组的解，那么称该一元一次方程为该不等式组的“相伴方程”．例如：方程 $2 x - 7 = 1$ 的解为 $x = 4$ ，不等式组 ${\begin{array}{l} x - 5 < 0, \\ 3 x > 6 \end{array}$ 的解集为 $2 < x < 5$ ．因为 $2 < 4 < 5$ ，所以 $2 x - 7 = 1$ 是不等式组 ${\begin{array}{l} x - 5 < 0, \\ 3 x > 6 \end{array}$ 的“相伴方程”．

(1)、若不等式组为 ${\begin{array}{l} x - 3 < 1 \\ x + 2 \leq 0 \end{array}$ ，则方程 $2 (x - 1) + 7 = 1$ 是不是该不等式组的相伴方程，请说明理由；

(2)、若关于x的方程 $2 x - a = 1$ 是不等式组 ${\begin{array}{l} 3 x - 2 > 3 + x \\ x - 3 \geq 2 x - 6 \end{array}$ 相伴方程，求a的取值

(3)、若方程 $5 x + 10 = 0$ 和 $\frac{2 x - 4}{3} = - 2$ 都是关于x的不等式组 ${\begin{array}{l} k x - 2 x < k - 2 \\ x + 5 \geq k \end{array} (k \neq 2)$ 的相伴方程，求k的取值范围．

查看试题解析
17. 定义：如果平行四边形的一组对边之和等于一条对角线的长时，我们称这个四边形为“沙漏四边形”．

(1)、当沙漏四边形是矩形时，两条对角线所夹锐角为度；

(2)、如图，在沙漏四边形ABCD中，对角线AC、BD相交于点O ，满足 $A B + C D = B D$ ，且 $A B ⊥ B D$ ，过点B、D分别作 $B E ⊥ A C$ ， $D F ⊥ A C$ ，垂足为E、F ，连接DE、BF ，所得四边形BEDF也是沙漏四边形．若 $B E = 1$ ，求BC的长以及 $△ B F C$ 的面积．

查看试题解析
18. 定义： $a, b, c$ 为正整数，若 $c^{2} = a^{2} + b^{2}$ ，则称 $c$ 为“完美勾股数”， $a, b$ 为 $c$ 的“伴侣勾股数”．如 $1 3^{2} = 5^{2} + 1 2^{2}$ ，则13是“完美勾股数”，5，12是13的“伴侣勾股数”．

(1)、数10“完美勾股数”（填“是”或“不是”）；

(2)、已知 $△ A B C$ 的三边 $a, b, c$ 满足 $a^{2} + b^{2} + c^{2} - 6 a - 8 b - 10 c + 50 = 0$ ．求证： $c$ 是“完美勾股数”．

查看试题解析
19. 定义新运算：对于任意实数a ， b都有 $a \oplus b = a (a - b) + 1$ ，如： $2 \oplus 5 = 2 (2 - 5) + 1 = - 5$ ，请求出不等式 $4 \oplus x \geq 2$ 的正整数解．

查看试题解析
20. 我们定义，关于同一个未知数的不等式A和B，若A的解都是B的解，则称A与B存在“雅含”关系，且A不等式称为B不等式的“子式”．如 $A ： x ＜ 0 ， B ： x ＜ 1$ ，满足A的解都是B的解，所以A与B存在“雅含”关系，A是B的“子式”．

(1)、若关于x的不等式 $A ： x + 2 ＞ 1 ， B ： x ＞ 3$ ，请问A与B是否存在“雅含”关系，若存在，请说明谁是谁的“子式”；

(2)、已知关于x的不等式C： $\frac{x - 1}{2} < \frac{a + 1}{3}$ ， D： $2 x - （ 3 - x ）＜ 3$ ，若C与D存在“雅含”关系，且C是D的“子式”，求a的取值范围；

(3)、已知 $2 m + n ＝ k ， m - n ＝ 3 ， m \geq \frac{1}{2} ， n ＜ - 1$ ，且k为整数，关于x的不等式 $P ： k x + 6 ＞ x + 4 ， Q ： 6 （ 2 x - 1 ） \leq 4 x + 2$ ，请分析是否存在k，使得P与Q存在“雅含”关系，且Q是P的“子式”，若存在，请求出k的值，若不存在，请说明理由．

查看试题解析
21. 定义新运算“★”和“#”如下： $a ★ b = a b + b$ ， $a # b = a b - a^{2}$ ．例如： $1 ★ 2 = 1 \times 2 + 2 = 4$ ， $1 # 3 = 1 \times 3 - 1^{2} = 2$ ．

(1)、计算 $[(- \frac{1}{2}) ★ (- \frac{1}{3})] # 6$ ；

(2)、已知 ${\begin{cases} (- 2) ★ x < 0 \\ 3 # (- x) \geq - 21 \end{cases}$ 是关于x的不等式组，求该不等式组的所有整数解的中位数．

查看试题解析
22. 定义运算 min{a，b}：当 a≥b 时，min{a，b}＝b；当 a＜b 时，min{a，b}＝a；如：min{4，0}＝0；min{2，2}＝2；min{﹣3，﹣1}＝﹣3．根据该定义运算完成下列问题：

(1)、min{﹣3，2}＝，当 x≤3 时，min{x，3}＝；

(2)、如图，已知直线 y₁＝x+m 与 y₂＝kx﹣2 相交于点 P（﹣2，1），若 min{x+m，kx﹣2}＝kx﹣2，结合图象，直接写出 x 的取值范围是；

(3)、若 min{3x﹣1，﹣x+3}＝3﹣x，求 x 的取值范围．

查看试题解析
23. 我们新定义一种三角形：两边的平方和等于第三边平方的2倍的三角形叫可爱三角形．

(1)、①根据“可爱三角形”的定义，请判断：等边三角形一定（填“是”或“不是”）可爱三角形；
②若三角形的三边长分别是4， $2 \sqrt{6}$ ， $2 \sqrt{5}$ ，则该三角形（填“是”或“不是”）可爱三角形；

(2)、若 $Rt △ A B C$ 是可爱三角形， $∠ C = 90 °$ ， $A C = 2 \sqrt{2}$ ，求 $A B$ 的长．

查看试题解析
24. 【阅读】
定义：如果一个三角形有两个内角的差为90°，那么这样的三角形叫做“准直角三角形”．

(1)、【理解】
①若 $∠ A = 60 °$ ， $∠ B = 15 °$ ，则 $△ A B C$ “准直角三角形”；（填“是”或“不是”）
②已知 $△ A B C$ 是“准直角三角形”，且 $∠ C > 90 °$ ， $∠ A = 40 °$ ，则 $∠ B$ 的度数为．

(2)、【应用】
如图，在 $△ A B C$ 中，点D在 $A C$ 上，连接 $B D$ ．若 $B D = A D$ ， $A C = 18$ ， $B C = 12$ ， $A D ： C D = 5 ： 13$ ，试说明 $△ A B C$ 是“准直角三角形”．

查看试题解析