命题新趋势5 新定义——2024年北师大版数学七(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 定义一种新运算,当时, . 若 , 则的值为( )A、 B、4 C、4或 D、4或2. 定义一种新运算 , 那么的运算结果为( )A、 B、 C、 D、3. 定义 , 则方程的解为( )A、 B、 C、 D、4. 设 , 是实数,定义一种新运算: , 下面有四个推断:
;
;
;
.
其中所有正确推断的序号是( )
A、 B、 C、 D、5. 若定义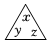 表示 ,
表示 ,  表示 , 则运算
表示 , 则运算
 的结果为( ) A、 B、 C、 D、6. 设a、b是有理数,定义一种新运算:a*b=(a﹣b)2 , 下面有四个推断:①a*b=b*a;②(a*b)2=a2*b2;③(﹣a)*b=a*(﹣b);④a*(b+c)=a*b+a*c . 其中正确推断的序号是( )A、①③ B、①② C、①③④ D、①②③④7. 若定义
的结果为( ) A、 B、 C、 D、6. 设a、b是有理数,定义一种新运算:a*b=(a﹣b)2 , 下面有四个推断:①a*b=b*a;②(a*b)2=a2*b2;③(﹣a)*b=a*(﹣b);④a*(b+c)=a*b+a*c . 其中正确推断的序号是( )A、①③ B、①② C、①③④ D、①②③④7. 若定义 表示xyz,
表示xyz, 表示 , 则运算
表示 , 则运算 的结果为( ) A、 B、 C、 D、8. 定义 , 例如.则的结果为( )A、 B、 C、 D、9. 对任意两个实数a,b定义两种运算:a⊕b , a⊗b , 并且定义运算顺序仍然是先做括号内的,例如(﹣2)⊕3=3,(﹣2)⊗3=﹣2,[(﹣2)⊕3]⊗2=2,那么(⊕2)⊗的值为( )A、2 B、 C、3 D、310. 定义:平面内的直线与相交于点O,对于该平面内任意一点M,点M到直线、的距离分别为a、b,则称有序非负实数对是点M的“距离坐标”,根据上述定义,“距离坐标”为的点的个数有( ).
的结果为( ) A、 B、 C、 D、8. 定义 , 例如.则的结果为( )A、 B、 C、 D、9. 对任意两个实数a,b定义两种运算:a⊕b , a⊗b , 并且定义运算顺序仍然是先做括号内的,例如(﹣2)⊕3=3,(﹣2)⊗3=﹣2,[(﹣2)⊕3]⊗2=2,那么(⊕2)⊗的值为( )A、2 B、 C、3 D、310. 定义:平面内的直线与相交于点O,对于该平面内任意一点M,点M到直线、的距离分别为a、b,则称有序非负实数对是点M的“距离坐标”,根据上述定义,“距离坐标”为的点的个数有( ). A、1个 B、2个 C、3个 D、4个11. 我们定义一个新运算: , 如 , 那么为( )A、 B、 C、 D、3212. 定义新运算:对于任意实数a,b都有 , 等式右边是常用的乘法和减法运算.规定,若 , , 则的值为( )A、-2 B、-4 C、-7 D、-1113. 设 , 是实数,定义@的一种运算如下:@ ,则下列结论:①若@=0,则或;②@(+z)=@+@z;③不存在实数 , , 满足@;④设 , 是矩形的长和宽,若矩形的周长固定,则当时,@最大,其中正确的是( )A、①②③ B、①②④ C、①③④ D、②③④
A、1个 B、2个 C、3个 D、4个11. 我们定义一个新运算: , 如 , 那么为( )A、 B、 C、 D、3212. 定义新运算:对于任意实数a,b都有 , 等式右边是常用的乘法和减法运算.规定,若 , , 则的值为( )A、-2 B、-4 C、-7 D、-1113. 设 , 是实数,定义@的一种运算如下:@ ,则下列结论:①若@=0,则或;②@(+z)=@+@z;③不存在实数 , , 满足@;④设 , 是矩形的长和宽,若矩形的周长固定,则当时,@最大,其中正确的是( )A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
14. 现定义一种运算“⊕”,对任意有理数m , n规定: , 如: , 则的值是 .15. 定义新运算“※”:A※.例如(2)※按照这种运算法则,若(x+2)※(2-x)=20,则 x=.16. 定义一种运算:若 , 则称;计算 .17. 定义运算 , 若 , 则的值为 .18. 定义一种新运算: a★b=ab-a2 , 则x★(x+y)= .19. 定义一种新的运算:规定 , 则 .20. 定义运算:a⊕b=(a+b)(a-3),下面给出这种运算的四个结论:①4⊕5=9;②a⊕b=b⊕a;③若a⊕b=0,则a+b=0;④若a+b=0,则a⊕b=0.其中正确的结论是(把所有正确结论的序号都填在横线上)
三、实践探究题
-
21. 对于整数a , b定义新运算;(其中m , n为常数),如 .(1)、当 , 时,的值为;(2)、若 , , 求的值.22. 定义新运算 =ad+3b-2c,如 =1×7+3×5-2×3=7+15-6=16。
(1)、计算 的值。
(2)、化简: 。
23. 定义:任意两个数 , , 按规则运算得到一个新数 , 称所得的新数为 , 的“和积数”.(1)、若 , , 求 , 的“和积数”;(2)、若 , , 求 , 的“和积数”;(3)、已知 , 且 , 的“和积数” , 求用含的式子表示并计算的最小值.24. 【问题背景】现定义一种新运算“⊙”对任意有理数m,n,规定: .例如: .
(1)、【问题推广】先化简,再求值: , 其中 , ;
(2)、【拓展提升】若 , 求p,q的值
25. 定义:对任意一个两位数 , 如果满足个位数字与十位数字互不相同,且都不为零那么称这个两位数为“互异数”.将一个“互异数”的个位数字与十位数字对调后得到一个新的两位数,把这个新两位数与原两位数的和与11的商记为 . 例如: , 对调个位数字与十位数字得到新两位数21,新两位数与原两位数的和为 , 和与11的商为 , 所以 . 根据以上定义,回答下列问题:(1)、①下列两位数:50,44,35中,“互异数”为;②计算:;(2)、一个“互异数”的十位数字是 , 个位数字是 , 且 , 求的值;(3)、如果一个“互异数”的十位数字是 , 个位数字是 , 且 , 求“互异数”的值.26. 规定两数a , b之间的一种运算,记作 , 如果 , 则 . 我们叫为“雅对”.例如:因为 , 所以 . 我们还可以利用“雅对”定义说明等式成立.证明如下:设 , , 则 , , 故 , 则 , 即 .
(1)、根据上述规定,填空:=;( , 16)=4;(2)、计算= , 并说明理由;(3)、利用“雅对”定义说明: , 对于任意非0整数n都成立.