命题新趋势5 新定义——2024年浙教版数学八(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 我们把形如a+b(a,b为有理数,为最简二次根式)的数叫做型无理数,如2+3是型无理数,则()2是( )A、型无理数 B、型无理数 C、型无理数 D、型无理数2. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]=x2的解为( )
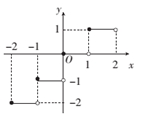 A、0或 B、0或2 C、1或﹣ D、或﹣3. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”.有以下关于倍根方程的说法:
A、0或 B、0或2 C、1或﹣ D、或﹣3. 如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另外一个根的2倍,则称这样的方程为“倍根方程”.有以下关于倍根方程的说法:①方程x2−x−2=0是倍根方程;②若(x−2)(mx+n)=0是倍根方程:则4m2+5mn+n2=0;③若p,q满足pq=2,则关于x的方程px2+3x+q=0是倍根方程;
④若方程以ax2+bx+c=0是倍根方程,则必有2b2=9ac.
其中正确的有( )个
A、1 B、2 C、3 D、44. 定义:cx2+bx+a=0是一元二次方程ax2+bx+c=0的倒方程,下列四个结论中,错误的是( )A、如果x=2是x2+2x+c=0的倒方程的解,则c= B、如果ac<0,那么这两个方程都有两个不相等的实数根 C、如果一元二次方程ax2-2x+c=0无解,则它的倒方程也无解 D、如果一元二次方程ax2+bx+c=0有两个不相等的实数根,则它的倒方程也有两个不相等的实数根5. 定义运算“★”:对于任意实数a,b,都有 ★ = .若 , 则 ★ 的值为( )A、0 B、 C、 D、56. 定义新运算: 例如 ,则函数 的图象大致是( )A、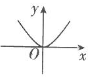 B、
B、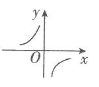 C、
C、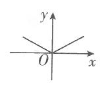 D、
D、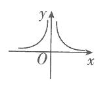 7. 用[x]表示不大于x的最大整数,则方程 的解的个数为( )A、1 B、2 C、3 D、4
7. 用[x]表示不大于x的最大整数,则方程 的解的个数为( )A、1 B、2 C、3 D、4二、填空题
-
8. 对于实数a , b , 定义运算“”:例如: , 因为 , 所以 . 若是一元二次方程的两个根,则 .9. 新定义:关于的一元二次方程与称为“同族二次方程”.例如:与是“同族二次方程”,现有关于的一元二次方程与是“同族二次方程”,则代数式的最小值是 .10. 定义菱形的两条对角线长之比为“对角线比”.(1)、若菱形成为正方形,则“对角线比”为 ;(2)、当“对角线比”为4,菱形面积为800时,菱形的边长为 .11. 对于实数m , n , 我们定义一种运算为:m※n=mn+m﹣n , 则(a+b)※(a﹣b)= , 则方程x※(2※x)=﹣3的解是 .12. 如图,定义:若菱形 AECF 与正方形ABCD的两个顶点A,C重合,另外两个顶点E,F在正方形ABCD 的内部,则称菱形AECF 为正方形ABCD 的内含菱形.若正方形的周长为16,其内含菱形的边长是整数,则内含菱形的周长为;若正方形的面积为18,其内含菱形的面积为6,则内含菱形的边长为.

三、实践探究题
-
13. 定义:对角线互相垂直的四边形叫做“垂美”四边形.
了解性质:如图1:已知四边形ABCD中,AC⊥BD . 垂足为O , 则有:AB2+CD2=AD2+BC2;

(图1) (图2) (图3)

(图4) (图5)
(1)、性质应用:如图1,四边形ABCD是垂美四边形,若AD=2,BC=4,CD=3,则AB=;(2)、性质变式:如图2,图3,P是矩形ABCD所在平面内任意一点,则有以下重要结论:AP2+CP2=BP2+DP2 . 请以图3为例将重要结论证明出来.(3)、应用变式:①如图4,在矩形ABCD中,O为对角线交点,P为BO中点,则;(写出证明过程)②如图5,在∆ABC中,CA=4,CB=6,D是∆ABC内一点,且CD=2,∠ADB=90°,则AB的最小值是.
14. 定义:一个四边形的四条边和两条对角线这六条线段中只有两种长度,我们把这样的四边形叫做双距四边形.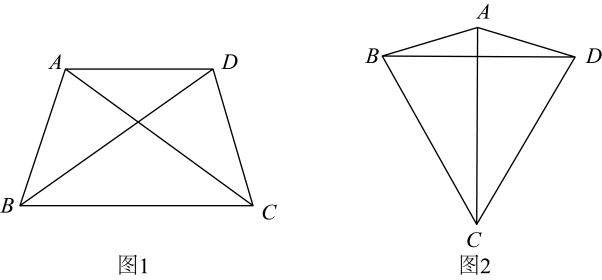 (1)、下列说法正确的有(填序号).
(1)、下列说法正确的有(填序号).①正方形一定是双距四边形.
②矩形一定是双距四边形.
③有一个内角为的菱形是双距四边形.
(2)、如图1,在四边形中, , , , 求证:四边形为双距四边形.(3)、如图2,四边形为双距四边形, , , , 求的长.15. 定义:数学活动课上,陈老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做它的对等四边形. (1)、在图1,图2中,点A、B、C都在格点(小正方形的顶点)上,请在图1,图2中各画一个以格点为顶点,AB、BC为边的一个对等四边形ABCD(两个图形不全等);(2)、如图3,对等四边形ABCD中,∠ADC=90°,AB=BD=CD=10,AD=12,求BC的长.16. 定义:我们将与称为一对“对偶式”,因为
(1)、在图1,图2中,点A、B、C都在格点(小正方形的顶点)上,请在图1,图2中各画一个以格点为顶点,AB、BC为边的一个对等四边形ABCD(两个图形不全等);(2)、如图3,对等四边形ABCD中,∠ADC=90°,AB=BD=CD=10,AD=12,求BC的长.16. 定义:我们将与称为一对“对偶式”,因为, 所以构造“对偶式”再将其相乘可以有效的将中的“根号”去掉,于是二次根式除法可以这样计算:如.像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
根据以上材料,理解并运用材料提供的方法,解答以下问题:
(1)、对偶式与之间的关系为____.A、互为相反数 B、互为倒数 C、绝对值相等 D、没有任何关系(2)、已知 , , 求的值.(3)、解方程:(提示:利用“对偶式”相关知识,令).17. 定义:我们把对角线相等的四边形叫做和美四边形. (1)、请举出一种你所学过的特殊四边形中是和美四边形的例子.(2)、如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;(3)、如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,∠AOB=60°,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.18. 我们定义:只有一组对角相等的凸四边形叫做等对角四边形.
(1)、请举出一种你所学过的特殊四边形中是和美四边形的例子.(2)、如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;(3)、如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,∠AOB=60°,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.18. 我们定义:只有一组对角相等的凸四边形叫做等对角四边形. (1)、四边形ABCD是等对角四边形,A≠C,若A=50°,B=100°,则C= , D= .(2)、图①、图②均为4×4的正方形网格,线段AB、BC的端点均在格点上,按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.(3)、如图③,在平行四边形ABCD中,A=60°,AB=12,AD=6,点E为AB的中点,过点E作EFDC,交DC于点F.点P是射线FE上一个动点,设FP=x,求以点A、D、E、P为顶点的四边形为等对角四边形时x的值.19. 定义:对角线相等的四边形称为对美四边形.
(1)、四边形ABCD是等对角四边形,A≠C,若A=50°,B=100°,则C= , D= .(2)、图①、图②均为4×4的正方形网格,线段AB、BC的端点均在格点上,按要求以AB、BC为边在图①、图②中各画一个等对角四边形ABCD.要求:四边形ABCD的顶点D在格点上,且两个四边形不全等.(3)、如图③,在平行四边形ABCD中,A=60°,AB=12,AD=6,点E为AB的中点,过点E作EFDC,交DC于点F.点P是射线FE上一个动点,设FP=x,求以点A、D、E、P为顶点的四边形为等对角四边形时x的值.19. 定义:对角线相等的四边形称为对美四边形. (1)、我们学过的对美四边形有、 . (写出两个)(2)、如图1,D为等腰△ABC底边AB上的一点,连结CD,过C作 , 以B为顶点作交CF于点E,求证:四边形CDBE为对美四边形.(3)、如图2,对美四边形ABCD中,对角线AC、BD交于点O,AC=BD, .
(1)、我们学过的对美四边形有、 . (写出两个)(2)、如图1,D为等腰△ABC底边AB上的一点,连结CD,过C作 , 以B为顶点作交CF于点E,求证:四边形CDBE为对美四边形.(3)、如图2,对美四边形ABCD中,对角线AC、BD交于点O,AC=BD, .①若 , , 求四边形ABCD的面积.
②若 , 设 , , 试求出y与x的关系式.
20. 定义:把横、纵坐标均为整数的点称为整点。如图,反比例函数y= (×>0)与正比例函数y=×相交于整点A,与一次函数y=-x+t相交于整点B、C,正比例函数y=x与一次函数y=-x+t相交于点D,线段BC与线段AD上的整点个数之比记作m.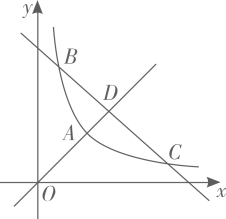 (1)、当k=4时,求D点的坐标和m值.(2)、当线段BC上的整点个数为7,AD=时,求t的值.(3)、当AD≤时,请直接写出t与m之间的关系式.21. 定义:只有三边相等的四边形称为准菱形.
(1)、当k=4时,求D点的坐标和m值.(2)、当线段BC上的整点个数为7,AD=时,求t的值.(3)、当AD≤时,请直接写出t与m之间的关系式.21. 定义:只有三边相等的四边形称为准菱形.
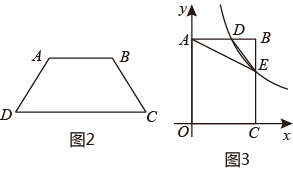 (1)、如图1,图形 (填序号)是准菱形;(2)、如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;(3)、如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y= (k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.
(1)、如图1,图形 (填序号)是准菱形;(2)、如图2,四边形ABCD中,AB∥DC,∠B+∠D=180°,AB=AD,求证:四边形ABCD是准菱形;(3)、如图3,在平面直角坐标系xOy中,矩形OABC的边OA,OC分别落在y轴,x轴上,反比例函数y= (k>0)的图象分别与边AB,BC交于点D,E.已知AD=DE,△ADE的面积为10,AD:DB=5:3,若点F是坐标平面上一点,四边形ADEF是准菱形,当准菱形ADEF面积最大时,求点F的坐标.