命题新趋势5 新定义——2024年浙教版数学七(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、选择题
-
1. 定义:两个自然数的平方和加上这两个自然数乘积的两倍即可得到一个新的自然数,我们把这个新的自然数称为“完全数”.例如:22+32+2×2×3=25,其中“25”就是一个“完全数”.则任取两个自然数可得到小于200且不重复的“完全数”的个数有( )A、14个 B、15个 C、26个 D、60个2. 定义:如果关于 x的分式方程 的解等于 我们就说这个方程是差解方程.如:就是一个差解方程.如果关于x的分式方程-2是一个差解方程,那么m的值为( )A、2 B、 C、 D、-23. 若定义
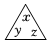 表示 ,
表示 ,  表示 , 则运算
表示 , 则运算
 的结果为( ) A、 B、 C、 D、4. 我们规定:表示不超过的最大整数,例如: , , 则关于和的二元一次方程组的解为( )A、 B、 C、 D、5. 对x,y定义一种新运算“※”,规定:x※y=mx+ny(其中m,n均为非零常数),若1※1=4,1※2=3.则2※1的值是( )A、3 B、5 C、9 D、116. 对x,y定义一种新运算“&”,规定:x&y=mx+ny(其中m,n均为非零常数),若1&1=3,1&2=4.则2&(-1)的值是( )A、0 B、2 C、3 D、57. 若定义
的结果为( ) A、 B、 C、 D、4. 我们规定:表示不超过的最大整数,例如: , , 则关于和的二元一次方程组的解为( )A、 B、 C、 D、5. 对x,y定义一种新运算“※”,规定:x※y=mx+ny(其中m,n均为非零常数),若1※1=4,1※2=3.则2※1的值是( )A、3 B、5 C、9 D、116. 对x,y定义一种新运算“&”,规定:x&y=mx+ny(其中m,n均为非零常数),若1&1=3,1&2=4.则2&(-1)的值是( )A、0 B、2 C、3 D、57. 若定义 表示 ,
表示 ,  表示 , 则运算
表示 , 则运算 ÷
÷ 的结果为( ) A、 B、 C、 D、8. 设m,n为实数,定义如下一种新运算:m☆n=若关于x的方程a(x☆x)=(x☆12)+1无解,则a的值是( )A、4 B、-3 C、4或-3 D、4或3
的结果为( ) A、 B、 C、 D、8. 设m,n为实数,定义如下一种新运算:m☆n=若关于x的方程a(x☆x)=(x☆12)+1无解,则a的值是( )A、4 B、-3 C、4或-3 D、4或3二、填空题
-
9. 定义一种新运算: a★b= . 若3★m= , 则m的值为10. 对于 , 定义一种新运算( , 是非零常数).例如 . 若 , , 则 , .11. 定义一种新的运算: , 例如: , 那么
(1)若 , 那么;
(2)若 , 且关于x,y的二元一次方程 , 当a,b取不同值时,方程都有一个公共解,那么公共解为 .
12. 定义一种新的运算:a☆b=2a-b,例如:3☆(-1)=2×3-(-1)=7。若a☆b=0,且关于x,y的二元一次方程(a+1)x-by-a+3=0,当a,b取不同值时,方程都有一个公共解,那么这个公共解为13. 定义:若一个正整数能表示为两个连续自然数的平方差,那么就称这个正整数为“优数”,如1,3,5都是优数,则位于1到400之间的所有优数之和为.14. 定义:对于三个不是同类项的单项式A,B,C,若 可以写成 的形式,则称这三项为“完全搭配项”,若单项式 ,4和m是完全搭配项,则m可能是.(写出所有情况)15. 定义一种新运算“※”,规定 ※ = ,其中 、 为常数,且1※2=5,2※1=3,则2※3=.三、解答题
-
16. 小明在数学课外小组活动中遇到这样一个“新定义”问题:
定义运算“※”为:a※b= , 求1※(﹣4)的值.
小明是这样解决问题的:由新定义可知a=1,b=﹣4,又b<0,所以1※(﹣4)=
请你参考小明的解题思路,回答下列问题:
(1)计算:3※7;
(2)若15※m= , 求m的值;
17. 将4个数a b c d排成两行,两列,两边各加一条竖直线记成 , 定义=ad﹣bc.上述记号叫做2阶行列式,若=7x.求x的值.18. 对于实数a、b,定义一种新运算“⊗”为:a⊗b= , 这里等式右边是通常的四则运算.例如:1⊗3== .(1)解方程(﹣2)⊗x=1⊗x;
(2)若x,y均为自然数,且满足等式y﹣5= , 求满足条件的所有数对(x,y).
四、综合题
-
19. 阅读下列材料:
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: .我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: 这样的分式就是假分式;再如: 这样的分式就是真分式.类似地,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: 这样的分式就是假分式;再如: 这样的分式就是真分式.类似地,假分式也可以化为带分式(即:整式与真分式的和的形式).
奾: ;
再如:
解决下列问题:
(1)、分式 是分式(填“真”或“假”);(2)、假分式 可化为带分式的形式;(3)、如果分式 的值为整数,那么 的整数值为.20. 对a , b定义一种新运算T , 规定:T(a , b)=(a+2b)(ax+by)(其中x , y均为非零实数).例如:T(1,1)=3x+3y .(1)、已知T(1,-1)=0,T(0,2)=8,求x , y的值;(2)、已知关于x , y的方程组 , 若a≥-2,求x+y的取值范围;(3)、在(2)的条件下,已知平面直角坐标系上的点A(x , y)落在坐标轴上,将线段OA沿x轴向右平移2个单位,得线段O′A′,坐标轴上有一点B满足三角形BOA′的面积为9,请直接写出点B的坐标.21. 定义:如果一个正整数能表示为两个连续偶数的平方差,那么我们称这个正整数为“和谐数”.如4=22-02 , 12=42-22 , 20=62-42 , 因此,4,12,20这三个数都是“和谐数”.(1)、当28=m2-n2时,m+n=;(2)、设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构成的“和谐数”是4的倍数吗?为什么?22. 【项目学习】配方法是数学中重要的一种思想方法,它是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法,这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.例如,把二次三项式进行配方
解:
我们定义:一个整数能表示成(a,b是整数)的形式,则称这个数为“完美数”例如,5是“完美数”,理由:因为 , 再如, , (x,y是整数)所以M也是“完美数”
(1)、【问题解决】下列各数中,“完美数”有 . (填序号)
①10 ②45 ③28 ④29
(2)、若二次三项式(是整数)是“完美数”,可配方成(m,为常数),则的值为;(3)、【问题探究】已知(x,y是整数,k是常数),要使S为“完美数”,试求出符合条件的k的值.
(4)、【问题拓展】已知实数x,y满足 , 求的最小值.
23. 对 , 定义一种新运算: .例如:当 , 时, .
(1)、若 , , 求和的值;(2)、若是非负数, , 求的取值范围.五、实践探究题
-
24. 规定两数a , b之间的一种运算,记作 , 如果 , 则 . 我们叫为“雅对”.例如:因为 , 所以 . 我们还可以利用“雅对”定义说明等式成立.证明如下:
设 , , 则 , , 故 , 则 , 即 .
(1)、根据上述规定,填空:=;( , 16)=4;(2)、计算= , 并说明理由;(3)、利用“雅对”定义说明: , 对于任意非0整数n都成立.25.
【阅读理解】
本学期第五章学习了《平行线的判定》,认识了同位角,内错角、同旁内角及它们的定义.学会了平行线的三个判定方法.
判定方法一:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
判定方法二:内错角相等,两直线平行;
判定方法三:同旁内角互补,两直线平行.
(1)、如图(1),请你找出一对同位角;一对内错角是;一对同旁内角是.(说明:以上填空只找出一对即可)(2)、【新知学习】如图(2),我们把∠2与∠8叫作外错角,请结合学习的同位角、内错角、同旁内角定义,给外错角下个定义:;
(3)、在图(1)中找出另一对外错角是____A、∠1与∠6 B、∠1与∠7 C、∠2与∠5 D、∠2与∠7(4)、请你结合图(2),证明命题:“外错角相等,两直线平行”.如图(2),已知:直线a,b被c所截,∠2=∠8.
求证:a∥b.
证明: