命题新趋势4 分类讨论思想——2024年北师大版数学八（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 等腰三角形中一个外角等于100°，则另两个内角的度数分别为（　　）

A、40°，40° B、80°，20° C、50°，50° D、50°，50°或80°，20°

查看试题解析
2. 等腰三角形一腰上的高与另一腰的夹角是50°，则这个等腰三角形的底角为（）

A、70° B、20° C、70°或20° D、40°或140°

查看试题解析
3. 在 $▱ A B C D$ 中， $A B = 3$ ， $B E$ 平分 $∠ A B C$ 交 $A D$ 于点E ，若点E分 $A D$ 为 $1 : 3$ 两部分，则 $D E$ 的长为（）

A、1 B、1或9 C、4 D、4或12

查看试题解析
4. 若关于x的分式方程 $\frac{2}{x - 1} + \frac{m x}{(x - 1) (x + 2)} = \frac{1}{x + 2}$ 有增根，则m的值为（）

A、1.5 B、-6 C、1或-2 D、1.5或-6

查看试题解析
5. 等腰三角形的一条边长为4，另一条边长为7，则该三角形的周长为（）

A、15 B、18 C、15或18 D、18或23

查看试题解析
6. 若等腰三角形的一个外角度数为100°，则该等腰三角形顶角的度数为（　　）

A、80° B、100° C、20°或100° D、20°或80°

查看试题解析
7. 若关于x的方程 $\frac{m x - 1}{x - 1} = 3$ 无解，则m的值为（）

A、1 B、1或3 C、1或2 D、2或3

查看试题解析
8. 在矩形 $A B C D$ 中，点 $M$ 是对角线 $B D$ 上一点， $A B = 3$ ， $B C = 4$ ，当 $△ A M D$ 为等腰三角形时， $B M$ 的长为（）

A、1 B、2.5 C、1.5或2 D、1或2.5

查看试题解析
9. 在平行四边形ABCD中有一个内角为50°，则∠A的度数为（）

A、50° B、100° C、50°或100° D、50°或130°

查看试题解析
10. 若关于x的分式方程 $\frac{2 m}{x - 1} + \frac{m}{x + 1} = \frac{4}{x^{2} - 1}$ 有增根，则m的值为（）

A、1 B、-2 C、1或 $- 2$ D、 $- 1$ 或2

查看试题解析

二、填空题

11. 等腰三角形的周长是 $13 c m$ ，其中一边长是 $5 c m$ ，则该等腰三角形的腰长为．

查看试题解析
12. 已知等腰三角形的两边长分别是3和7，则这个等腰三角形的周长为．

查看试题解析
13. 如果等腰三角形有一个角是 $30 °$ ，那么它的顶角是．

查看试题解析
14. 若等腰三角形中有一个角为 $52 °$ ，则它的一条腰上的高与底边的夹角的度数为．

查看试题解析
15. 在平行四边形ABCD中，∠BAD的平分线交直线CD于点E，∠ABC的平分线交直线CD于点F，AD＝5，EF＝2，则线段AB的长为.

查看试题解析
16. 已知平行四边形的三个顶点的坐标分别为 $O (0, 0)$ 、 $A (2, 0)$ 、 $B (1, 1)$ ，则第四个顶点 $C$ 的坐标是．

查看试题解析

三、解答题

17. 定义：如果一元一次方程的解也是一元一次不等式组的解，则称该一元一次方程为该不等式组的“相伴方程”，例如：方程 $2 x - 6 = 0$ 的解为 $x = 3$ ，不等式组 ${\begin{array}{l} x - 2 > 0 \\ x < 5 \end{array}$ 的解为 $2 < x < 5$ ，因为 $2 < 3 < 5$ ，所以称方程 $2 x - 6 = 0$ 为不等式组 ${\begin{array}{l} x - 2 > 0 \\ x \leq 5 \end{array}$ 的“相伴方程”．

(1)、下列方程是不等式组 ${\begin{array}{l} x + 1 > 0 \\ x < 2 \end{array}$ 的“相伴方程”的是；（填序号）
① $x - 1 = 0$ ；② $2 x + 1 = 0$ ；③ $- 2 x - 2 = 0$ ．

(2)、若关于x的方程 $2 x - k = 2$ 是不等式组 ${\begin{array}{l} 3 x - 6 > 4 - x \\ x - 1 \geq 4 x - 10 \end{array}$ 0的“相伴方程”，求k的取值范围；

(3)、若方程 $2 x + 6 = 0$ ， $\frac{2 x - 1}{3} = - 1$ 都是关于x的不等式组 ${\begin{cases} (m - 1) x < m - 1 \\ x + 5 \geq m \end{cases}$ 的“相伴方程”，其中 $m \neq 1$ ，求m的取值范围．

查看试题解析
18. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， D为 $A B$ 中点，点E在直线 $B C$ 上（点E不与点B ， C重合），连接 $D E$ ，过点D作 $D F ⊥ D E$ 交直线 $A C$ 于点F ，连接 $E F$ ．

(1)、如图1，当点F与点A重合时，请直接写出线段 $E F$ 与 $B E$ 的数量关系：．

(2)、如图2，当点F不与点A重合时，请写出线段 $A F$ ， $E F$ ， $B E$ 之间的数量关系，并说明理由；

(3)、若 $A C = 5$ ， $B C = 3$ ， $E C = 1$ ，请直接写出线段AF的长．

查看试题解析
19. 我们定义，关于同一个未知数的不等式A和B，若A的解都是B的解，则称A与B存在“雅含”关系，且A不等式称为B不等式的“子式”．如 $A ： x ＜ 0 ， B ： x ＜ 1$ ，满足A的解都是B的解，所以A与B存在“雅含”关系，A是B的“子式”．

(1)、若关于x的不等式 $A ： x + 2 ＞ 1 ， B ： x ＞ 3$ ，请问A与B是否存在“雅含”关系，若存在，请说明谁是谁的“子式”；

(2)、已知关于x的不等式C： $\frac{x - 1}{2} < \frac{a + 1}{3}$ ， D： $2 x - （ 3 - x ）＜ 3$ ，若C与D存在“雅含”关系，且C是D的“子式”，求a的取值范围；

(3)、已知 $2 m + n ＝ k ， m - n ＝ 3 ， m \geq \frac{1}{2} ， n ＜ - 1$ ，且k为整数，关于x的不等式 $P ： k x + 6 ＞ x + 4 ， Q ： 6 （ 2 x - 1 ） \leq 4 x + 2$ ，请分析是否存在k，使得P与Q存在“雅含”关系，且Q是P的“子式”，若存在，请求出k的值，若不存在，请说明理由．

查看试题解析

四、综合题

20. 如图，直线 $y = \frac{4}{3} x + 8$ 和直线 $y = k x + b$ 都经过x轴负半轴上一点B ，分别与y轴的交点分别为A、C ，且 $O B = 2 O C$ ．

(1)、求直线 $C B$ 的解析式；

(2)、点E在x轴上， $△ A B E$ 为等腰三角形，请直接写出点E的坐标．

查看试题解析
21. 如图，在平面直角坐标系中，一次函数 $y = a x + b (a \neq 0)$ 的图象与x轴交于点 $A (- 2 ， 0)$ ，与y轴交于点C，且与正比例函数 $y = 2 x$ 的图象交于点 $B (2 ， 4)$ ．

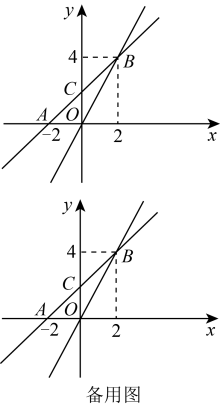(1)、求一次函数 $y = a x + b (a \neq 0)$ 的解析式；

(2)、点M在x轴上，当 $M B + M C$ 最小时，求点M的坐标；

(3)、若D是直线AB上一点，E是平面内一点，以O、C、D、E四点为顶点的四边形是矩形，请直接写出点E的坐标．

查看试题解析
22. 如图，在平面直角坐标系中，直线 $y = k x + b$ 与 $x$ 轴、 $y$ 轴相交于 $A (6 ， 0)$ ， $B (0 ， 3)$ 两点，动点 $C$ 在线段 $O A$ 上，将线段 $C B$ 绕着点 $C$ 顺时针旋转 $90 °$ 得到 $C D$ ，此时点 $D$ 恰好落在直线 $A B$ 上，过点 $D$ 作 $D E ⊥ x$ 轴于点 $E$ ．

(1)、求直线 $y = k x + b$ 的表达式

(2)、试确定点 $D$ 的坐标；

(3)、若点 $P$ 在 $y$ 轴上，点 $Q$ 在直线 $A B$ 上，是否存在以 $C$ ， $D$ ， $P$ ， $Q$ 为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的 $Q$ 点坐标，若不存在，请说明理由．

查看试题解析

五、实践探究题

23. 定义：如果一元一次方程的解也是一元一次不等式组的解，那么称该一元一次方程为该不等式组的“相伴方程”．例如：方程 $2 x - 7 = 1$ 的解为 $x = 4$ ，不等式组 ${\begin{array}{l} x - 5 < 0, \\ 3 x > 6 \end{array}$ 的解集为 $2 < x < 5$ ．因为 $2 < 4 < 5$ ，所以 $2 x - 7 = 1$ 是不等式组 ${\begin{array}{l} x - 5 < 0, \\ 3 x > 6 \end{array}$ 的“相伴方程”．

(1)、若不等式组为 ${\begin{array}{l} x - 3 < 1 \\ x + 2 \leq 0 \end{array}$ ，则方程 $2 (x - 1) + 7 = 1$ 是不是该不等式组的相伴方程，请说明理由；

(2)、若关于x的方程 $2 x - a = 1$ 是不等式组 ${\begin{array}{l} 3 x - 2 > 3 + x \\ x - 3 \geq 2 x - 6 \end{array}$ 相伴方程，求a的取值

(3)、若方程 $5 x + 10 = 0$ 和 $\frac{2 x - 4}{3} = - 2$ 都是关于x的不等式组 ${\begin{array}{l} k x - 2 x < k - 2 \\ x + 5 \geq k \end{array} (k \neq 2)$ 的相伴方程，求k的取值范围．

查看试题解析