命题新趋势4 纠错思想——2024年北师大版数学七（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 在一次数学活动课上，老师让同学们借助一副三角尺画平行线 $A B ， C D$ ．下图是小楠、小曼两位同学的作法．关于两位同学的作法，下面说法正确的是（）

A、仅小楠的作法正确
B、仅小曼的作法正确 C、两位同学的作法都不正确 D、两位同学的作法都正确

查看试题解析
2. 甲、乙、丙共同完成这样一道题目：“直线 $A B$ ， $C D$ 相交于点 $O$ ， $O D$ 平分 $∠ B O F$ ， $O E ⊥ C D$ ，垂足为 $O$ （如图所示）．若 $∠ E O F = α$ ，请用含 $α$ 的代数式表示 $∠ A O C$ ， $∠ B O E$ ， $∠ A O F$ 中任意两个角的度数．”甲的结果是 $∠ A O C = α - 90 °$ ， $∠ B O E = \frac{2}{3} α$ ；乙的结果是 $∠ B O E = 180 ° - α$ ， $∠ A O F = 360 ° - 2 α$ ；丙的结果是 $∠ A O C = α - 90 °$ ， $∠ A O F = 360 ° - α$ ．下列判断正确的是（）

A、甲对乙错 B、甲和乙都错 C、乙和丙都对 D、乙对丙错

查看试题解析
3. 小明和小亮一起研究一道数学题，如图，BD⊥AC于点D，E是边BC 上的一点，过点 E作 EF⊥AC于点F，点G在AB上，连结DG，GE.小明说：“如果还知道∠GDB=∠FEC，则能得到∠AGD=∠ABC.”小亮说：“如果∠AGD=∠ABC，可得到∠GDB=∠FEC.”下列判断正确的是（）

A、小明的说法正确，小亮的说法错误 B、小明的说法正确，小亮的说法正确 C、小明的说法错误，小亮的说法正确 D、小明的说法错误，小亮的说法错误

查看试题解析

4. 数学课上，老师要求同学们利用三角板画出两条平行线，老师展示了甲、乙两位同学的画法如下：

甲的画法：

①将含 $30 °$ 角的三角尺的最长边与直线a重合，另一块三角尺最长边与含 $30 °$ 角的三角尺的最短边紧贴；

②将含 $30 °$ 角的三角尺沿贴合边平移一段距离，画出最长边所在直线b，则 $b ∥ a$ ．

乙的画法：

①将含 $30 °$ 角三角尺的最长边与直线a重合，用虚线作出一条最短边所在直线；

②再次将含 $30 °$ 角三角尺最短边与虚线重合，画出最长边所在直线b，则 $b ∥ a$ ．

请你判断两人的作图的正确性（）

A、甲正确，乙错误 B、甲错误，乙正确 C、两人都正确 D、两人都错误

查看试题解析

5. 小明和小亮在研究一道数学题，如图 $E F ⊥ A B$ ， $C D ⊥ A B$ ，垂足分别为E、D，G在 $A C$ 上．
小明说：“如果 $∠ C D G = ∠ B F E$ ，则能得到 $∠ A G D = ∠ A C B$ ”；
小亮说：“连接 $F G$ ，如果 $F G / / A B$ ，则能得到 $∠ G F C = ∠ A D G$ ”．
则下列判断正确的是（）

A、小明说法正确，小亮说法错误 B、小明说法正确，小亮说法正确 C、小明说法错误，小亮说法正确 D、小明说法错误，小亮说法错误

查看试题解析
6. 小明、小亮、小刚、小颖一起研究一道数学题，如图，BD⊥AC与点D，点E是BC边上的一动点，过E作EF⊥AC与点F，点G在AB上，连DG，GE.
小明说：“如果还知道∠GDB＝∠FEC，则能得到∠AGD＝∠ABC.”
小亮说：“如果∠AGD＝∠ABC，可得到∠GDB＝∠FEC.”
则下列判断正确的是（）

A、小明说法正确，小亮说法错误 B、小明说法正确，小亮说法正确 C、小明说法错误，小亮说法正确 D、小明说法错误，小亮说法错误

查看试题解析
7. 如图，把 $A B ， C D ， E F$ 三根木条钉在一起，使之可以在连接点M，N处自由旋转，若 $∠ 1 = 50 °$ ， $∠ 2 = 60 °$ ，则如何旋转木条 $A B$ 才能使它与木条 $C D$ 平行.
小明说：把木条 $A B$ 绕点M逆时针旋转10°；
小刚说：把木条 $A B$ 绕点M顺时针旋转170°.
以下说法正确的是（）

A、小明的操作正确，小刚的操作错误 B、小明的操作错误，小刚的操作正确 C、小明和小刚的操作都正确 D、小明和小刚的操作都错误

查看试题解析
8. 在多项式 $16 x^{2} + 1$ 添加一个单项式，使得到的多项式能运用完全平方公式分解因式，则下列表述正确的是（）
嘉琪：添加 $\pm 8 x$ ， $16 x^{2} + 1 \pm 8 x = {(4 x \pm 1)}^{2}$
陌陌：添加 $64 x^{4}$ ， $64 x^{4} + 16 x^{2} + 1 = {(8 x^{2} + 1)}^{2}$
嘟嘟：添加 $- 1$ ， $16 x^{2} + 1 - 1 = 16 x^{2} = {(4 x)}^{2}$

A、嘉琪和陌陌的做法正确 B、嘉琪和嘟嘟的做法正确 C、陌陌和嘟嘟的做法正确 D、三位同学的做法都错误

查看试题解析
9. 如图，点 $E$ ， $F$ 分别在直线 $A B$ ， $C D$ 上，点 $G$ ， $H$ 在两直线之间，线段 $E F$ 与 $G H$ 相交于点 $O$ ，且有 $∠ A E F + ∠ C F E = 180 °$ ， $∠ 1 = ∠ 2$ ．三人说法如下：甲： $A B ∥ C D$ ；乙： $G E ∥ F H$ ；丙： $A B ∥ G H$ ．下列判断正确的是（）

A、甲错，乙对 B、甲对，乙错 C、甲对，丙对 D、乙对，丙错

查看试题解析
10. 定义：当点C在线段AB上， $A C = n A B$ 时，我们称 $n$ 为点C在线段AB上的点值，记作 $d_{C ※ A B} = n$ .
甲同学猜想：点C在线段AB上，若 $A C = 2 B C$ ，则 $d_{C ※ A B} = \frac{2}{3}$ .
乙同学猜想：点C是线段AB的三等分点，则 $d_{C ※ A B} = \frac{1}{3}$
关于甲乙两位同学的猜想，下列说法正确的是（）

A、甲正确，乙不正确 B、甲不正确，乙正确 C、两人都正确 D、两人都不正确

查看试题解析
11. 如图1，将边长为 $a$ 的大正方形前去一个边长为 $b$ 的小正方形，并沽图中的虚线㮍开，拼接后得到图2，根据图形的面积，甲同学写出了一个等式 $a^{2} -$ $b^{2} = (a + b) (a - b)$ ，乙同学也写出了一个等式 ${(a - b)}^{2}$ $= a^{2} - 2 a b + b^{2}$ ，则（）

A、甲、乙都正确 B、甲、乙都不正确 C、甲正确，乙不正确 D、甲不正确，乙正确

查看试题解析

12. 数学老师要求学生用一张长方形的纸片

A B C D

折出一个

45 °

的角，甲、乙两人的折法如下，下列说法正确的是（）

甲：如图1，将纸片沿折痕 $A E$ 折叠，使点B落在 $A D$ 上的点 $B^{'}$ 处， $∠ E A D$ 即为所求．
乙：如图2，将纸片沿折痕 $A E ， A F$ 折叠，使B，D两点分别落在点 $B^{'} ， D^{'}$ 处，且 $A B^{'}$ 与 $A D^{'}$ 在同一直线上， $∠ E A F$ 即为所求．

A、甲和乙的折法都正确 B、只有甲的折法正确 C、只有乙的折法正确 D、甲和乙的折法都不正确

查看试题解析

二、解答题

13. 为了解学生对所学知识的应用能力，某校老师在七年级数学兴趣小组活动中，设置了这样的问题：因为池塘两端A ， B的距离无法直接测量，请同学们设计方案测量A ， B的距离．甲、乙两位同学分别设计出了如下两种方案：
甲：如图1，在平地上取一个可以直接到达点A ， B的点O ，连接 $A O$ 并延长到点C ，连接 $B O$ 并延长到点D ，使 $C O = A O$ ， $D O = B O$ ．连接 $D C$ ，测出 $D C$ 的长即可．
乙：如图2，先确定直线 $A B$ ，过点B作直线 $B E$ ，在直线 $B E$ 上找可以直接到达点A的一点D ，连接 $D A$ ，作 $∠ A D B = ∠ B D C$ ，交直线 $A B$ 于点C ，最后测量 $B C$ 的长即可．

(1)、甲、乙两同学的方案哪个可行？

(2)、请说明你认为方案可行的理由：
以上的生活情景化归到数学上：根据题意，此时，
已知条件是：；有待说明的是：；
请介绍你每一步的思考及相应的道理：

(3)、请将不可行的方案稍加修改使之可行．
你的修改是：

查看试题解析
14. 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题，甲同学认为该命题是真命题，并作图如图1所示，已知 $A B ∥ D E$ ， $B C ∥ D F$ ， BC与DE交于点G．

(1)、根据甲同学的作图及题设，求证：∠B＝∠D；

(2)、乙同学对甲同学的判断提出质疑，认为该命题不一定成立，是假命题，并作图如图2所示，题设与甲同学相同，得到 $∠ B \neq ∠ D$ ，根据乙同学的作图，试判断∠B与∠D的数量关系，并说明理由．

(3)、综合甲、乙两同学的探究，两边分别平行的两个角的数量关系是：．

查看试题解析
15. 某数学兴趣小组探究命题“两边分别平行的两个角相等”是否是真命题，甲同学认为该命题是真命题，并作图如图1所示，已知AB∥DE，AC∥DF，AC与DE交于点G．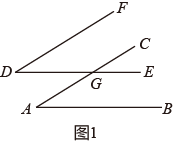

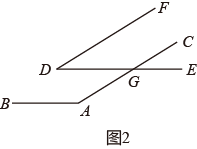(1)、根据甲同学的作图及题设，求证：∠A＝∠D；

(2)、乙同学对甲同学的判断提出质疑，认为该命题不一定成立，是假命题，并作图如图2所示，题设与甲同学相同，得到∠A≠∠D，根据乙同学的作图，试判断∠A与∠D的数量关系，并说明理由．

查看试题解析