命题新趋势4 纠错思想——2024年浙教版数学八（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图是一张平行四边形纸片ABCD，要求利用所学知识将它裁剪成一个菱形．甲、乙两位同学的作法如下：
甲：连结AC，作AC的中垂线，交AD，BC于点E，F，则四边形AFCE是菱形．
乙：作 $∠ A$ 与 $∠ B$ 的平分线AE，BF，分别交BC于点 $E$ ，交AD于点 $F$ ，则四边形ABEF的菱形.
对于甲、乙两人的作法，下列判断正确的是（）

A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙均正确 D、甲、乙均错误

查看试题解析
2. 在一次活动课中，对如图所示的平行四边形（AD＞AB）进行折叠，第一次沿着AE折叠，点B落在点F处，接着两组同学分别尝试了两种不同的二次折叠，并给出了判断：组1：若沿着CF的中垂线折叠，则点D与点A必重合；组2：若沿着DF折叠，AD与DC所在的直线重合，且点A的对应点仍落在直线AF上，则 $\frac{S_{Δ A B F}}{S ▭_{C F A D}}$ ＝ $\frac{1}{3}$ （）

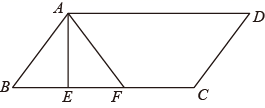A、组1判断正确，组2判断正确 B、组1判断正确，组2判断错误 C、组1判断错误，组2判断正确 D、组1判断错误，组2判断错误

查看试题解析
3. 如图，要在平行四边形 $A B C D$ 内作一个菱形.甲，乙两位同学的作法分别如下：

对于甲乙两人的作法，可判断（）

A、甲正确，乙错误 B、甲错误，乙正确 C、甲，乙均正确 D、甲、乙均错误

查看试题解析
4. 如图，在一张平行四边形纸片ABCD中，画一个菱形，甲、乙两位同学的画法如下：
甲：以B ， A为圆心，AB长为半径作弧，分别交BC ， AD于点E ， F ，则四边形ABEF为菱形；乙：作∠A ， ∠B的平分线AE ， BF ，分别交BC于点E ，交AD于点F ，则四边形ABEF是菱形；关于甲、乙两人的画法，下列判断正确的是（）

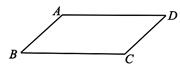A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误

查看试题解析
5.
如图，是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：对于甲、乙两人的作法，可判断（　　）

A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙均正确 D、甲、乙均错误

查看试题解析
6. 如图1，直线 $l_{1} ∥ l_{2}$ ，直线 $l_{3}$ 分别交直线 $l_{1}$ ， $l_{2}$ 于点A，B．小嘉在图1的基础上进行尺规作图，得到如图2，并探究得到下面两个结论：
①四边形ABCD是邻边不相等的平行四边形；②四边形ABCD是对角线互相垂直的平行四边形．下列判断正确的是（）

A、①②都正确 B、①错误，②正确 C、①②都错误 D、①正确，②错误

查看试题解析
7. 探讨关于x的一元二次方程 $a x^{2} + b x - 1 = 0$ 总有实数根的条件，下面三名同学给出建议：甲：a，b同号；乙： $a - b - 1 = 0$ ；丙： $a + b - 1 = 0$ ．其中符合条件的是（）

A、甲，乙，丙都正确 B、只有甲错误 C、甲，乙，丙都错误 D、只有乙正确

查看试题解析
8. 如图，在四边形ABCD中， $A B ∥ D C$ ， $A B = A D$ ，对角线AC，BD交于点O，AC平分 $∠ B A D$ ，过点C作 $C E ⊥ A B$ 交AB的延长线与点E，连接OE．
嘉嘉说：“四边形ABCD是菱形．”
琪琪说：“ $O E = \frac{1}{2} A C$ ． ”
对于他俩的说法，正确的是（）

A、嘉嘉正确，琪琪错误 B、嘉嘉错误，琪琪正确 C、他俩都正确 D、他俩都错误

查看试题解析
9. 在化简 $\frac{x - y}{\sqrt{x} + \sqrt{y}}$ 时，甲、乙两位同学的解答如下：
甲： $\frac{x - y}{\sqrt{x} + \sqrt{y}} = \frac{(x - y) (\sqrt{x} - \sqrt{y})}{(\sqrt{x} + \sqrt{y}) (\sqrt{x} - \sqrt{y})} = \frac{(x - y) (\sqrt{x} - \sqrt{y})}{{(\sqrt{x})}^{2} - {(\sqrt{y})}^{2}} = \sqrt{x} - \sqrt{y}$ ；
乙： $\frac{x - y}{\sqrt{x} + \sqrt{y}} = \frac{{(\sqrt{x})}^{2} - {(\sqrt{y})}^{2}}{\sqrt{x} + \sqrt{y}} = \frac{(\sqrt{x} - \sqrt{y}) (\sqrt{x} + \sqrt{y})}{\sqrt{x} + \sqrt{y}} = \sqrt{x} - \sqrt{y}$ .
这两位同学的解法，你认为（）

A、两人解法都对 B、甲错乙对 C、甲对乙错 D、两人都错

查看试题解析
10. 在将式子 $\frac{m}{\sqrt{m}}$ （m＞0）化简时，
小明的方法是： $\frac{m}{\sqrt{m}}$ = $\frac{m^{} \sqrt{m}}{\sqrt{m} \cdot \sqrt{m}}$ = $\frac{m \sqrt{m}}{m}$ = $\sqrt{m}$ ；

小亮的方法是： $\frac{m}{\sqrt{m}} = \frac{{(\sqrt{m})}^{2}}{\sqrt{m}} = \sqrt{m}$ ；

小丽的方法是： $\frac{m}{\sqrt{m}} = \frac{\sqrt{m^{2}}}{\sqrt{m}} = \sqrt{\frac{m^{2}}{m}} = \sqrt{m}$ .

则下列说法正确的是（　　）

A、小明、小亮的方法正确，小丽的方法错误 B、小明、小丽的方法正确，小亮的方法错误 C、小明、小亮、小丽的方法都正确 D、小明、小丽、小亮的方法都错误

查看试题解析
11. 将图1中两个三角形按图2所示的方式摆放，其中四边形 $A B C D$ 为矩形，连接 $P Q$ ， $M N$ ，甲、乙两人有如下结论：
甲：若四边形 $A B C D$ 为正方形，则四边形 $P Q M N$ 必是正方形；
乙：若四边形 $P Q M N$ 为正方形，则四边形 $A B C D$ 必是正方形．
下列判断正确的是（）

A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙都错误 D、甲、乙都正确

查看试题解析
12. 在将式子 $\frac{m}{\sqrt{m}}$ （m＞0）化简时，
小明的方法是： $\frac{m}{\sqrt{m}}$ = $\frac{m^{} \sqrt{m}}{\sqrt{m} \cdot \sqrt{m}}$ = $\frac{m \sqrt{m}}{m}$ = $\sqrt{m}$ ；
小亮的方法是： $\frac{m}{\sqrt{m}} = \frac{{(\sqrt{m})}^{2}}{\sqrt{m}} = \sqrt{m}$ ；
小丽的方法是： $\frac{m}{\sqrt{m}} = \frac{\sqrt{m^{2}}}{\sqrt{m}} = \sqrt{\frac{m^{2}}{m}} = \sqrt{m}$ .
则下列说法正确的是（　　）

A、小明、小亮的方法正确，小丽的方法错误 B、小明、小丽的方法正确，小亮的方法错误 C、小明、小亮、小丽的方法都正确 D、小明、小丽、小亮的方法都错误

查看试题解析

二、解答题

13. 甲、乙两位同学解方程 $2 (x - 2) = (x - 2)^{2}$ 的过程如下框：
甲： $2 (x - 2) = (x - 2)^{2}$
两边同除以 $(x - 2)$ 得：
$2 = x - 2$
则 $x = 4$
（）
乙：
移项得 $2 (x - 2) - (x - 2)^{2} = 0$
提公因式 $(x - 2) (2 - x - 2) = 0$
则 $x - 2 = 0$ 或 $2 - x - 2 = 0$
$∴ x_{1} = 2, x_{2} = 0$
（）
你认为他们的解法是否正确？若正确请在括号内打“√”，若错误打“×”，并写出你的解答过程．

查看试题解析
14. 阅读下列文字，回答问题．
题目：在Rt△ABC中，∠C=90°，若∠A≠45°，所以AC≠BC．
证明：假设AC=BC，因为∠A≠45°，∠C=90°，所以∠A≠∠B．
所以AC≠BC，这与假设矛盾，所以AC≠BC．
上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正．

查看试题解析
15. 下面是小明解一元二次方程 $2 x (x - 5) = 3 (5 - x)$ 的过程：
解：原方程可化为 $2 x (x - 5) = - 3 (x - 5)$ ， ……第一步

方程两边同除以 $(x - 5)$ 得， $2 x = - 3$ ， ……第二步

系数化为1得 $x = - \frac{3}{2}$

小明的解答是否正确？若正确，请说明理由；若不正确，请指出从第几步开始出现错误，分析出现错误的原因，并写出正确的解答过程

查看试题解析
16. 在解一元二次方程 ${(5 x - 3)}^{2} = 5 x - 3$ 时，小王的解答如下：
解：方程两边同时除以 $5 x - 3$ 得： $5 x - 3 = 1$ ；
移项得： $5 x = 4$ ；
解得： $x = \frac{4}{5}$ ．
小王的解题过程是否正确？若正确，请在框内打“√”；若错误，写出正确解答．

查看试题解析
17. 阅读下列文字，回答问题。
题目：如图，在Rt△ABC中，∠C=90°，若∠A≠45°，则AC≠BC.

证明：假设AC=BC，

$∵$ ∠A≠45°，∠C=90°，∴∠A≠∠B

∴AC≠BC，这与假设矛盾，∴AC≠BC.

上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正。

查看试题解析
18. 下面是小华同学解答题目的过程：
$\sqrt{\frac{9}{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$

$= \frac{\sqrt{9}}{\sqrt{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}}) \dots \dots$ 第一步．

$= \frac{3 \sqrt{2}}{2} - 2 \sqrt{3} \times 2 \sqrt{6} + 2 \sqrt{3} \times 3 \sqrt{\frac{2}{3}} \dots \dots$ 第二步．

$= \frac{3 \sqrt{2}}{2} - 12 \sqrt{2} + 6 \sqrt{2} \dots \dots$ 第三步．

$= \frac{9 \sqrt{2}}{2} \dots \dots$ 第四步．

小华的解题过程是否有错误？如果有，请写出正确解答过程．

查看试题解析
19. 圆圆与方方两位同学解方程 $3 (x - 3) = (x - 3)^{2}$ 的过程如下框：

圆圆：
两边同除以 $(x - 3) .$ 得
$3 = x - 3$ .
则 $x = 6$ .
方方：
移项，得 $3 (x - 3) - (x - 3)^{2} = 0$ .
提取公因式，得 $(x - 3) (3 - x - 3) = 0$ .
则 $x - 3 = 0$ 或 $3 - x - 3 = 0$ .
解得 $x_{1} = 3 . x_{2} = 0$ .
你认为他们的解法是否正确？若错误，请写出你认为正确的解答过程.

查看试题解析

20. 按要求解方程：

（ 1 ）小聪同学解方程的过程如下，请指出最早出现错误的步骤序号，并写出正确的解答过程.

2x（x﹣1）＝3（x﹣1）

解：两边除以（x﹣1），得2x＝3①

系数化为1，得x＝1.5②

最早出现错误的步骤序号：　

你的解答过程：

2x（x﹣1）＝3（x﹣1）

（ 2 ）小明同学解方程的过程如下，请指出最早出现错误的步骤序号，并写出正确的解答过程.

（x﹣3）²＝9

解：两边开平方，得x﹣3＝3①

移项，合并同类项，得x＝6②

最早出现错误的步骤序号：　

你的解答过程：

（x﹣3）²＝9

（ 3 ）解方程：

x²﹣4x﹣5＝0

查看试题解析

21. 下面是王鑫同学进行实数运算的过程，认真阅读并完成相应的问题：
$\sqrt{\frac{9}{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$
$= \frac{\sqrt{9}}{\sqrt{2}} - \sqrt{12} \times (\sqrt{24} + 3 \sqrt{\frac{2}{3}})$ ……第一步
$= \frac{3 \sqrt{2}}{2} - 2 \sqrt{3} \times 2 \sqrt{6} + 2 \sqrt{3} \times 3 \sqrt{\frac{2}{3}}$ ……第二步
$= \frac{3 \sqrt{2}}{2} - 12 \sqrt{2} + 6 \sqrt{2}$ ……第三步
$= \frac{9 \sqrt{2}}{2}$ ……第四步
①以上化简步骤中第一步化简的依据是：；
②第步开始出现错误，请写出错误的原因；
③该运算正确结果应是．

查看试题解析
22. 用配方法解一元二次方程： $2 x^{2} + 3 x + 1 = 0 .$ 小明同学的解题过程如下：

解： $x^{2} + \frac{3}{2} x + \frac{1}{2} = 0$

$x^{2} + \frac{3}{2} x + \frac{9}{4} - \frac{9}{4} + \frac{1}{2} = 0$ ，

$(x + \frac{3}{2})^{2} = \frac{7}{4}$ ，

$x + \frac{3}{2} = \pm \frac{\sqrt{7}}{2}$ ，

$x_{1} = - \frac{3 + \sqrt{7}}{2}$ ， $x_{2} = - \frac{3 - \sqrt{7}}{2}$ ．

小明的解题过程是否正确？若正确，请回答“对”；若错误，请写出你的解题过程．

查看试题解析

三、综合题

23. 老师布置了一个作业，如下：
已知：如图1 $▱ A B C D$ 的对角线 $A C$ 的垂直平分线 $E F$ 交 $A D$ 于点 $F$ ，交 $B C$ 于点 $E$ ，交 $A C$ 于点 $O$ ．求证：四边形 $A E C F$ 是菱形．

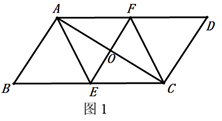
嘉琪同学写出了如图2所示的证明过程，老师说嘉琪同学的作业是错误的．请你解答下列问题：

(1)、能找出该同学错误的原因吗？请你指出来；

(2)、请你给出本题的符合题意证明过程．

查看试题解析

24. 王老师为了了解学生在数学学习中常见错误的纠正情况，收集整理了学生在作业和考试中的常见错误，编制了10道选择题，每题3分，对他所教的八年（1）班和八年（2）班进行了检测．如图所示表示从两班随机抽取的10名学生的得分情况：

(1)、利用图中提供的信息，补全如表：

班级	平均分（分）	中位数（分）	众数（分）
八年（1）班		24	24
八年（2）班	24

(2)、你认为那个班的学生纠错的得分情况比较整齐一些，通过计算说明理由．

查看试题解析

25. 老师布置了一个作业，如下：已知：如图1 $▱ A B C D$ 的对角线 $A C$ 的垂直平分线 $E F$ 交 $A D$ 于点F，交 $B C$ 于点E，交 $A C$ 于点O.求证：四边形 $A E C F$ 是菱形.

某同学写出了如图2所示的证明过程，老师说该同学的作业是错误的.请你解答下列问题：

(1)、能找出该同学错误的原因吗？请你指出来；

(2)、请你给出本题的符合题意证明过程.

查看试题解析

四、实践探究题

26. 发现思考：
已知等腰三角形ABC的两边长分别是方程x²-7x+10=0的两个根，求等腰三角形ABC 三条边的长各是多少.
下面是涵涵同学的作业，老师说他的做法有错误，请你找出错误之处并说明错误原因.
解 $x^{2} - 7 x + 10 = 0 ，$
a=1，b=-7，c=10.
∵b²-4ac=9>0，…………………①
$∴ x = \frac{- b \pm \sqrt{b^{2} - 4 a c}}{2 a} - \frac{7 \pm 3}{2} ，$ ……………………②
∴x₁=5，x₂=2…………………③
所以，当腰为5，底边为 2时，等腰三角形的三条边的长分别为5，5，2；⋯⋯⋯⋯⋯⋯⋯④
当腰为2，底边为5时，等腰三角形的三条边的长分别为2，2，5，⋯⋯⋯⋯⋯⋯⋯⑤

(1)、涵涵的作业错误的步骤是填序号)，错误的原因是

(2)、探究应用：
已知等腰三角形ABC的一腰和底边的长分别是关于x的方程 $x^{2} - m x + \frac{m}{2} - \frac{1}{4} = 0$ 的两个实数根.
①当m=2时，求△ABC的周长.
②当△ABC为等边三角形时，求m的值

查看试题解析