命题新趋势3 真实情境（2）——2024年北师大版数学八（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、因式分解

1. 因式分解 $x^{2} + m x + n$ 时，甲看错了 $m$ 的值，分解的结果是 $(x - 6) (x + 2)$ ，乙看错了 $n$ 的值，分解的结果为 $(x + 8) (x - 4)$ ，那么 $x^{2} + m x + n$ 分解因式正确的结果为（）

A、 $(x + 3) (x - 4)$ B、 $(x + 4) (x - 3)$ C、 $(x + 6) (x - 2)$ D、 $(x + 2) (x - 6)$

查看试题解析
2. 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息： $a - b$ ， $x - y$ ， $x + y$ ， $a + b$ ， $x^{2} - y^{2}$ ， $a^{2} - b^{2}$ 分别对应下列六个字，师、爱、我、保、好、美，现将 $(x^{2} - y^{2}) a^{2} - (x^{2} - y^{2}) b^{2}$ 因式分解．结果呈现的密码信息可能是（）

A、我爱美 B、保师好 C、爱我保师 D、美我保师

查看试题解析
3. 甲、乙两个同学因式分解 $x^{2} + a x + b$ 时，甲看错了a，分解结果为 $(x + 4) (x - 8)$ ，乙看错了b，分解结果为 $(x - 2) (x + 6)$ ．求多项式 $x^{2} + a x + b$ 分解因式的正确结果．

查看试题解析
4. 下面是某同学对 $(x^{2} - 2 x - 1) (x^{2} - 2 x + 3) + 4$ 进行因式分解的过程，解：设 $x^{2} - 2 x = y$
$原式$ = $(y - 1) (y + 3) + 4 \dots \dots \cdot 第一步$
= $y^{2} + 2 y + 1 \dots \dots 第二步$
= $(y + 1)^{2} \dots \dots 第三步$
= ${(x^{2} - 2 x + 1)}^{2} \dots \dots 第四步$
回答下列问题：

(1)、该同学第二步到第三步运用了
A．提取公因式
B．平方差公式
C．两数和的完全平方公式
D．两数差的完全平方公式

(2)、该同学因式分解的结果是否彻底？(填“彻底”或者“不彻底”)．若不彻底，请直接写出因式分解的最后结果

(3)、请你模仿以上方法尝试对多项式 $(x^{2} - 4 x) (x^{2} - 4 x + 8) + 16$ 进行因式分解．

查看试题解析
5. 【问题提出】如何分解因式：2x²+2xy-3x-3y？
【问题解决】某数学“探究学习”小组对以上问题进行了探究：
甲同学：2x²+2xy-3x-3y
=（2x²+2xy）-（3x+3y）
=2x（x+y）-3（x+y）
=（x+y）（2x-3）
乙同学：2x²+2xy-3x-3y
=（2x²-3x）+（2xy-3y）
=x（2x-3）+y（2x-3）
=（2x-3）（x+y）
【方法总结】将一个多项式适当分组后，利用提公因式法或运用公式法继续分解的方法叫做分组分解法．
【学以致用】尝试运用分组分解法解答下列问题：

(1)、分解因式：a²﹣b²+a﹣b；

(2)、已知△ABC的三边长a ， b ， c满足a²﹣ab+ac﹣bc＝0，判断△ABC的形状并说明理由．

(3)、【拓展提升】如图是一块长方形试验田，已知AB长为x m，AC长为（x+1）m，当x=a时，长方形试验田的面积为S₁m² ，当x=b时，长方形试验田的面积为S₂m²（a，b均为正整数），且满足S₂-S₁=8，请求出a和b的值．

查看试题解析
6. 【提出问题】某数学活动小组对多项式乘法进行如下探究：
$① (x + 2) (x + 3) = x^{2} + 5 x + 6$ ；
$② (x - 4) (x + 1) = x^{2} - 3 x - 4$ ；
$③ (y - 5) (y - 3) = y^{2} - 8 y + 15$ ．
通过以上计算发现，形如 $(x + p) (x + q)$ 的两个多项式相乘，其结果一定为 $x^{2} + (p + q) x + p q . (p ， q$ 为整数 $)$
因为因式分解是与整式乘法是方向相反的变形，所以一定有 $x^{2} + (p + q) x + p q = (x + p) (x + q)$ ，即可将形如 $x^{2} + (p + q) x + p q$ 的多项式因式分解成 $(x + p) (x + q) (p$ 、 $q$ 为整数 $)$ ．
例如： $x^{2} + 3 x + 2 = x^{2} + (1 + 2) x + 1 \times 2 = (x + 1) (x + 2)$ ．

(1)、【初步应用】用上面的方法分解因式： $x^{2} + 6 x + 8 =$ ；

(2)、【类比应用】规律应用：若 $x^{2} + m x + 8$ 可用以上方法进行因式分解，则整数 $m$ 的所有可能值是；

(3)、【拓展应用】分解因式： $(x^{2} - 4 x)^{2} - 2 (x^{2} - 4 x) - 15$ ．

查看试题解析

7. 下面是小林同学的数学学习笔记，请仔细阅读并完成相应的任务.

在因式分解中，把多项式中的某些部分看作是一个整体，用一个新的字母代替（即“换元”），这样不仅可以简化要分解的多项式的结构，而且能使式子的特点更加明显，便于观察如何进行因式分解，我们把这种因式分解的方法称为“换元法”.下面是小林同学用“换元法”对多项式 $(x^{2} - 2 x - 1) (x^{2} - 2 x + 3) + 4$ 进行因式分解的过程.

解：设 $x^{2} - 2 x = y$ .

原式 $= (y - 1) (y + 3) + 4$

$= y^{2} + 2 y + 1$

$= (y + 1)^{2}$

$= {(x^{2} - 2 x + 1)}^{2}$

任务：（1）小林同学因式分解的结果彻底吗？若不彻底，请你写出该因式分解的最后结果：____.

(1)、由平方的非负性可知

(x^{2} - 2 x - 1) (x^{2} - 2 x + 3) + 4

有最小值，则最小值为.

(2)、请你用“换元法”对多项式

(x^{2} + 6 x) (x^{2} + 6 x + 18) + 81

进行因式分解.

查看试题解析

8. 八年级课外兴趣小组活动时，老师提出了如下问题：将 $2 a - 3 a b - 4 + 6 b$ 因式分解．
【观察】经过小组合作交流，小明得到了如下的解决方法：
解法一：原式 $= (2 a - 3 a b) - (4 - 6 b) = a (2 - 3 b) - 2 (2 - 3 b) = (2 - 3 b) (a - 2)$ ；
解法二：原式 $= (2 a - 4) - (3 a b - 6 b) = 2 (a - 2) - 3 b (a - 2) = (a - 2) (2 - 3 b)$ ．
【感悟】对项数较多的多项式无法直接进行因式分解时，我们可以将多项式分为若干组，再利用提公因式法、公式法达到因式分解的目的，这就是因式分解的分组分解法．分组分解法在代数式的化简、求值及方程、函数等学习中起着重要的作用．（温馨提示：因式分解一定要分解到不能再分解为止）

(1)、【类比】请用分组分解法将 $x^{2} - a^{2} + x + a$ 因式分解；

(2)、【挑战】请用分组分解法将 $a x + a^{2} - 2 a b - b x + b^{2}$ 因式分解；

(3)、若 $a^{2} + b^{2} = 9$ ， $a - b = 2$ ，请用分组分解法先将 $a^{4} - 2 a^{3} b + 2 a^{2} b^{2} - 2 a b^{3} + b^{4}$ 因式分解，再求值．

查看试题解析

二、分式与分式方程

9. 数学家斐波那契编写的《算经》中有如下问题：一组人平分100元钱，每人分得若干，若再加上5人，平分150元钱，则第二次每人所得与第一次相同，求第二次分钱的人数．设第二次分钱的人数为x人，则可列方程为（）

A、 $100 x = 150 (x + 5)$ B、 $100 (x - 5) = 150 x$ C、 $\frac{100}{x} = \frac{150}{x + 5}$ D、 $\frac{100}{x - 5} = \frac{150}{x}$

查看试题解析
10. 某农场开挖一条长480米的渠道，开工后每天比原计划多挖20米，结果提前4天完成任务，若设原计划每天挖x米，那么下列方程中正确的是（）

A、 $\frac{480}{x - 20} - \frac{480}{x} = 4$ B、 $\frac{480}{x} - \frac{480}{x + 4} = 20$ C、 $\frac{480}{x} - \frac{480}{x + 20} = 4$ D、 $\frac{480}{x - 4} - \frac{480}{x} = 20$

查看试题解析
11. 2024年龙年春晚吉祥物“龙辰辰”引爆购买热潮，导致“一辰难求”．某工厂承接了 30万只吉祥物的生产任务，实际每天的生产效率比原计划提高了 $25 %$ ，提前 5 天完成任务．设原计划每天生产x万只吉祥物，则下面所列方程正确的是（）

A、 $\frac{30}{x} - \frac{30 \times (1 + 25 %)}{x} = 5$ B、 $\frac{30}{(1 + 25 %) x} - \frac{30}{x} = 5$ C、 $\frac{30 \times (1 + 25 %)}{x} - \frac{30}{x} = 5$ D、 $\frac{30}{x} - \frac{30}{(1 + 25 %) x} = 5$

查看试题解析
12. 一项工程，共有三种施工方案：①甲队单独完成这项工程，刚好如期完工；②乙队单独完成此项工程要比规定工期多用5天；③____，剩下的工程由乙队单独做，也正好如期完工．某同学设规定的工期为x天，根据题意列出了方程： $\frac{4}{x} + \frac{x}{x + 5} = 1$ ，则方案③中被墨水污染的部分应该是（　　）

A、甲乙合作了4天 B、甲先做了4天 C、甲先做了工程的 $\frac{1}{4}$ D、甲乙合作了工程的 $\frac{1}{4}$

查看试题解析
13. “绿水青山就是金山银山”.某地为美化环境，计划种植树木1000棵.由于志愿者的加入，实际每天植树的棵数比原计划增加了25%，结果提前2天完成任务.则实际每天植树棵.

查看试题解析
14. 我国是一个水资源贫乏的国家，每一个公民都应自觉养成节约用水的意识和习惯，为提高水资源的利用率，某住宅小区安装了循环用水装置．经测算，原来 $a$ 天用水 $b$ 吨，现在这些水可多用4天，现在每天比原来少用水吨．

查看试题解析
15. 二月开学季来临，某文具店在2月上旬推出了A、B、C三种不同主题的开学大礼包．已知二月上旬A、B、C三种主题大礼包售价之比为2：4：5，销量之比为7：1：2．开学后不久，根据市场需求，在二月下旬文具店老板对三种主题大礼包售价进行了调整，其中B主题大礼包售价比二月上旬降低了 $\frac{1}{4}$ ， C主题大礼包在2月上旬售价的基础上打八折，从而使得B、C两种主题大礼包销售额相较于二月上旬有所增加，A主题大礼包销售额相较于二月上旬有所下降．若A主题大礼包减少的销售额与B、C两种主题大礼包增加的销售额之比为4：7：5，且A主题大礼包减少的销售额占二月下旬三种主题大礼包总销售额的 $\frac{1}{16}$ ，则二月下旬B、C两种主题大礼包的销量之比为．

查看试题解析
16. 2024年龙年春晚吉祥物形象“龙辰辰”正式发布亮相，作为中华民族重要的精神象征和文化符号，千百年来，龙的形象贯穿文学、艺术、民俗、服饰、绘画等各个领域，也呈现了吉祥如意、平安幸福的美好寓意．吉祥物“龙辰辰”的产生受到众人的热捧．某工厂计划加急生产一批该吉祥物，决定选择使用A、B两种材料生产吉祥物．已知使用B材料的吉祥物比A材料每个贵50元，用3000元购买用A材料生产吉祥物的数量是用1500元购买B材料生产吉祥物数量的4倍．

(1)、求售卖一个A材料、一个B材料的吉祥物各需多少元？

(2)、一所中学为了激励学生奋发向上，准备用不超过3000元购买A、B两种材料的吉祥物共50个，来奖励学生．恰逢工厂对两种材料吉祥物的价格进行了调整：使用A材料的吉祥物的价格按售价的九折出售，使用B材料的吉祥物比售价提高了 $20 %$ ，那么该学校此次最多可购买多少个用B材料的吉祥物？

查看试题解析
17. 某书店制订了“读书节”活动计划，以下是活动计划的部分信息：
书本类别
A类
B类
进价（单位：元）
18
12
备注
用不超过16800元购进两类图书共1000本，A类图书不少于600本．

(1)、陈经理查看计划时发现：A类图书的标价是B类图书的1.5倍，若顾客用540元购买图书，单独购买A类图书的数量恰好比单独购买B类图书的数量少10本，请求出A，B两类图书的标价；

(2)、为了扩大影响，陈经理调整了销售方案：A类图书售价每本降低4元，B类图书价格不变．此时书店应如何进货才能获得最大利润？

查看试题解析

三、平行四边形

18. 如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得CD＝10m，则A，B之间的距离是（）

A、5m B、10m C、20m D、40m

查看试题解析
19. 如图所示，某居民小区为了美化居住环境，要在一块三角形 $A B C$ 空地上围一个四边形花坛 $B C F E$ ．已知点 $E$ 、 $F$ 分别是边 $A B$ 、 $A C$ 的中点，量得 $B C = 16$ 米，则边 $E F$ 的长是( )

A、6米 B、7米 C、8米 D、9米

查看试题解析
20. 2023年9月29日，中国航天局发布消息，探月工程嫦娥六号任务正按计划开展研制工作，将开展月球背面采样返回，计划于2024年上半年实施发射，对提升我国国际航天地位、推动航天技术创新、提供科学数据、培养人才和激发民众兴趣具有重要意义．如图登月探测器中，机械臂伸缩自如，灵活性强，其机械原理主要是运用了（）．

A、三角形的稳定性 B、平行四边形的不稳定性 C、两点之间线段最短 D、点到直线的距离垂线段最短

查看试题解析
21. 小敏不慎将一块平行四边形玻璃打碎成如图的四块，为了能在商店配到一块与原来相同的平行四边形玻璃，他带了两块碎玻璃，其编号应该是（　　）

A、①，② B、①，④ C、③，④ D、②，③

查看试题解析
22. 在平面直角坐标系中，已知点A（4，0），点B（﹣3，2），点C（0，2），点P从点B出发，以2个单位每秒的速度沿射线BC运动，点Q从点A出发，开始以1个单位每秒的速度向原点O运动，到达原点后立刻以原来3倍的速度沿射线OA运动，若P，Q两点同时出发，设运动时间为t秒，则当t＝时，以点A，Q，C，P为顶点的四边形为平行四边形．

查看试题解析
23. 一块四边形的绿化园地，四角都建有半径为2的圆形喷水池，则这四个喷水池占去的绿化园地的面积为。

查看试题解析
24. 阅读小明和小红的对话，解决下列问题.

(1)、这个“多加的锐角”是°.

(2)、小明求的是几边形的内角和？

(3)、若这是个正多边形，则这个正多边形的一个外角是多少度？

查看试题解析
25. 如图，在▱ABCD中，点O是对角线AC的中点．某数学学习小组要在AC上找两点E，F，使四边形BEDF为平行四边形，现总结出甲、乙两种方案如下：

甲方案

乙方案

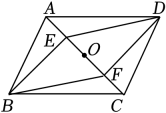
分别取AO，CO的中点E，F

作BE⊥AC于点E，DF⊥AC于点F

请回答下列问题：

(1)、以上方案能得到四边形BEDF为平行四边形的是 ▲ ，选择其中一种并证明，若不能，请说明理由；

(2)、若EF＝2AE，S_△_AED＝6，求▱ABCD的面积．

查看试题解析
26. 综合与实践课上，老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动．

(1)、操作判断：
如图1，在矩形 $A B C D$ 中，点 $E$ 为边 $A B$ 的中点，沿 $D E$ 折叠，使点 $A$ 落在点 $F$ 处，把纸片展平，延长 $D F$ 与 $B C$ 交于点 $G$ ．请写出线段 $F G$ 与线段 $B G$ 的数量关系，并说明理由.

(2)、迁移思考：
如图1，若 $A B = 4$ ，按照（1）中的操作进行折叠和作图，当 $C G = 2$ 时，求 $A D$ 的值.

(3)、拓展探索：
如图2，四边形 $A B C D$ 为平行四边形，其中 $∠ A$ 与 $∠ C$ 是对角，点 $E$ 为边 $A B$ 的中点，沿 $D E$ 折叠，使点 $A$ 落在点 $F$ 处，把纸片展平，延长 $D F$ 与射线 $B C$ 交于点 $G$ ．若 $A D = 2$ ， $C G = 0.5$ ，请直接写出线段 $D G$ 的值．

查看试题解析
27. 如图，在平行四边形ABCD中，点O是对角线AC的中点．某数学学习小组要在AC上找两点E，F，使四边形BEDF为平行四边形，现总结出甲、乙两种方案如下：

甲方案

乙方案

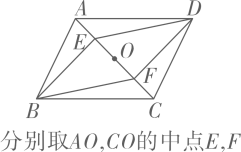
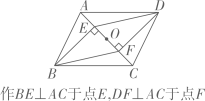
请回答下列问题：

(1)、以上方案能得到四边形BEDF为平行四边形的是甲方案或乙方案，选择其中一种并证明，若不能，请说明理由；

(2)、若EF=2AE， $S_{Δ A E D} = 6$ ，求平行四边形ABCD的面积.

查看试题解析

书本类别	A类	B类
进价（单位：元）	18	12
备注	用不超过16800元购进两类图书共1000本，A类图书不少于600本．

甲方案	乙方案