命题新趋势3 真实情境(2)——2024年北师大版数学七(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、三角形
-
1. 如图,为估计池塘两岸 , 间的距离,小明在池塘一侧选取了一点 , 测得 , , 那么间的距离不可能是( )
 A、 B、 C、 D、2. 如图,工人师傅砌门时,常用木条固定门框 , 使其不变形,这种做法的根据是( )
A、 B、 C、 D、2. 如图,工人师傅砌门时,常用木条固定门框 , 使其不变形,这种做法的根据是( ) A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性3. 健康骑行逐渐受到人们喜欢,图1是便携式折叠自行车,图2 是其示意图.AB∥CD , AE∥BD , CE平分∠ACD . 若∠D=70°,∠ACD=60°,则∠AEC=( )
A、两点之间线段最短 B、矩形的对称性 C、矩形的四个角都是直角 D、三角形的稳定性3. 健康骑行逐渐受到人们喜欢,图1是便携式折叠自行车,图2 是其示意图.AB∥CD , AE∥BD , CE平分∠ACD . 若∠D=70°,∠ACD=60°,则∠AEC=( ) A、80° B、90° C、100° D、110°4. 如图,一公路修到湖边时,需拐弯绕湖通过.第一个拐角 , 第二个拐角 . 如果道路与第一条路平行,则第三个拐角的度数是( )
A、80° B、90° C、100° D、110°4. 如图,一公路修到湖边时,需拐弯绕湖通过.第一个拐角 , 第二个拐角 . 如果道路与第一条路平行,则第三个拐角的度数是( ) A、 B、 C、 D、5. 如图所示的是一款手机支架,能非常方便地支起手机,由图分析这款手机支架的设计原理是三角形的 .
A、 B、 C、 D、5. 如图所示的是一款手机支架,能非常方便地支起手机,由图分析这款手机支架的设计原理是三角形的 . 6. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置下降30cm时,这时小明离地面的高度是cm.
6. 如图,小明与小红玩跷跷板游戏,如果跷跷板的支点(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置下降30cm时,这时小明离地面的高度是cm. 7. 有一座锥形小山,如图,要测量锥形小山两端、的距离,先在平地上取一个可以直接到达和的点 , 连接并延长到 , 使 , 连接并延长到 , 使 , 连接 , 量出的长为 , 则锥形小山两端、的距离为
7. 有一座锥形小山,如图,要测量锥形小山两端、的距离,先在平地上取一个可以直接到达和的点 , 连接并延长到 , 使 , 连接并延长到 , 使 , 连接 , 量出的长为 , 则锥形小山两端、的距离为 8. 如图是一种躺椅及其结构示意图,扶手AB与底座CD都平行于地面EF , 前支架OE与后支架OF分别与CD交于点G和点D , AB与DM交于点N , ∠AOE=∠BNM .
8. 如图是一种躺椅及其结构示意图,扶手AB与底座CD都平行于地面EF , 前支架OE与后支架OF分别与CD交于点G和点D , AB与DM交于点N , ∠AOE=∠BNM . (1)、请对说明理由;(2)、若OE平分∠AOF , ∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.9. 【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,中, , , 求边上的中线的取值范围.
(1)、请对说明理由;(2)、若OE平分∠AOF , ∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.9. 【阅读理解】课外兴趣小组活动时,老师提出了如下问题:如图1,中, , , 求边上的中线的取值范围.经过组内合作交流,小明得到了如下的解决方法:延长到点E , 使.请根据小明的方法思考:
 (1)、请证明(2)、请直接写出的取值范围;(3)、【问题解决】请利用上述方法(倍长中线)解决问题.
(1)、请证明(2)、请直接写出的取值范围;(3)、【问题解决】请利用上述方法(倍长中线)解决问题.如图2,已知 , , , P为的中点.若A , C , D共线,求证:平分;
10. 【背景】在同一平面内,两条直线的位置关系有两种,分别是平行和相交,在相交这种位置关系中包括垂直这种特殊位置关系. (1)、【应用】如图1,PQ//MN , A、B分别在PQ、MN上,AC平分∠PAB交MN于点C , D是直线MN上一点,AE平分∠BAD交MN于点E .
(1)、【应用】如图1,PQ//MN , A、B分别在PQ、MN上,AC平分∠PAB交MN于点C , D是直线MN上一点,AE平分∠BAD交MN于点E .①当D在点B的右侧,且∠ADC=30°,∠AEC=50°,∠BAD= ▲ °,∠PAC= ▲ °;
②过点E作EF⊥AC , 垂足为F , 记∠AEF=x度,∠ADB=y度,直接写出y与x的关系式.
(2)、【拓展】中欧班列是高质量共建“一带一路”的互联互通大动脉,中欧班列为了安全起见在某段铁路两旁安置了A , B两座可旋转探照灯.如图2,假定主道路是平行的,即PQ//MN ,连结AB , 且∠ABN=45°.灯A发出的射线AC自AQ顺时针旋转至AP便立即回转,灯B发出的射线BD自BM顺时针旋转至BN便立即回转,两灯不停交叉照射巡视.灯A转动的速度是3度/秒,灯B转动的速度是9度/秒,若它们同时开始转动,设转动时间为t秒,当灯A射线AC从AQ转至AP的过程中,AC与BD互相垂直时,请直接写出此时t的值.11. 如图1,自行车尾灯是由塑料罩片包裹的若干个小平面镜组成,利用平面镜反射光线,以提醒后方车辆注意.小亮所在学习小组对其工作原理进行探究,发现以下规律:如图2,为平面镜,分别为入射光线和反射光线,则 . 请继续以下探究: (1)、探究反射规律
(1)、探究反射规律①如图3, , 则 ▲ (用含的代数式表示).
②若光线 , 判断与的位置关系,并说明理由.
(2)、模拟应用研究在行驶过程中,后车驾驶员平视前方,且视点会高于反射点(如图4),因此小亮认为反射光线应与水平视线成一定角度.学习小组设计了如图5所示的模拟实验装置,使入射光线 , 当与所成夹角为时,求的度数.

二、轴对称
-
12. 一次数学活动中,检验两条纸带①、②的边线是否平行,嘉嘉和淇淇采用两种不同的方法:嘉嘉将纸带①沿折叠,量得;淇淇将纸带②沿折叠,发现与重合,与重合(点在上,点在上),如图所示.下列判断正确的是( )
 A、只有纸带①的边线平行 B、只有纸带②的边线平行 C、纸带①、②的边线都平行 D、纸带①、②的边线都不平行13. 第19届亚运会将于2022年9月在杭州举行,下列历届亚运会会徽是轴对称图形的是( )A、
A、只有纸带①的边线平行 B、只有纸带②的边线平行 C、纸带①、②的边线都平行 D、纸带①、②的边线都不平行13. 第19届亚运会将于2022年9月在杭州举行,下列历届亚运会会徽是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 14. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、
14. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、 B、
B、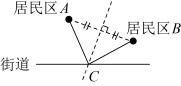 C、
C、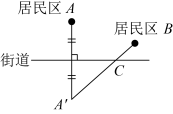 D、
D、 15. 折纸是一门古老而有趣的艺术,现代数学家们甚至为折纸建立了一套完整的“折纸几何学公理”.如图,小明在课余时间把一张长方形纸片沿折叠, , 则 .
15. 折纸是一门古老而有趣的艺术,现代数学家们甚至为折纸建立了一套完整的“折纸几何学公理”.如图,小明在课余时间把一张长方形纸片沿折叠, , 则 . 16. 在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD , 点E在AD上,点F在BC上,把长方形纸带沿EF折叠,若 , 则∠AEF= .
16. 在数学拓展课《折叠的奥秘》中,老师提出一个问题:如图,有一条长方形纸带ABCD , 点E在AD上,点F在BC上,把长方形纸带沿EF折叠,若 , 则∠AEF= . 17. 如图①是一把园林剪刀,把它抽象为图②,其中 . 若剪刀张开的角为 , 则°.
17. 如图①是一把园林剪刀,把它抽象为图②,其中 . 若剪刀张开的角为 , 则°. 18. 如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置。(保留作图痕迹)。
18. 如图,电信部门要在S区修建一座电视信号发射塔.按照设计要求,发射塔到两个城镇A,B距离必须相等,到两条高速公路m和n的距离也必须相等.发射塔应修建在什么位置?在图上标出它的位置。(保留作图痕迹)。 19. 问题解决:
19. 问题解决: (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.20.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.20. (1)、如图1,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.(2)、如图2,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O'N平分∠CO'F,试判断OM与O'N的位置关系,并说明理由.21. 综合与实践:折纸中的数学
(1)、如图1,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.(2)、如图2,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O'N平分∠CO'F,试判断OM与O'N的位置关系,并说明理由.21. 综合与实践:折纸中的数学【问题提出】在前面的学习中我们通过折纸可以找出一个角的平分线,还可以折出过一个点且与已知直线垂直的直线.那我们能否通过折纸的方式找到过直线外一点且与已知直线平行的直线呢?
 (1)、【知识初探】王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.
(1)、【知识初探】王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.①如图1,在纸上画出一条直线 , 在外取一点 . 过点折叠纸片,使得点的对应点落在直线上(如图2),记折痕与的交点为 , 将纸片展开铺平.则 ▲ ;
②再过点将纸片进行折叠,使得点的对应点落在直线上(如图3),再将纸片展开铺平(如图4).此时王玲说,就是的平行线.王玲的说法正确吗?请写出过程予以证明;
(2)、【拓展延伸】李强同学在王玲同学折纸的基础上,补充了条件:如图5,在线段上任取一点 , 连接 , 请你猜想与这三个角之间的数量关系,并说明理由.三、概率初步
-
22. 一个小球在如图所示的地板上自由滚动,并随机停留在某块方砖上,每块方砖的大小、质地完全相同,那么该小球停留在白色区域的概率是( )
 A、 B、 C、 D、23. 在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )
A、 B、 C、 D、23. 在同样的条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表,由表估计该麦种的发芽概率是( )试验种子数n(粒)
50
200
500
1000
3000
发芽频数m
45
188
476
951
2850
发芽频率
0.9
0.94
0.952
0.951
0.95
A、0.8 B、0.9 C、0.95 D、124. 某商场为了吸引顾客,设计了如图所示的可自由转动的转盘,当指针指向阴影部分时,顾客可获得一份奖品,那么顾客获奖的概率为( )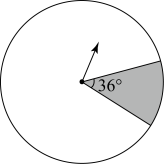 A、 B、 C、 D、25. 小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( )
A、 B、 C、 D、25. 小明做“用频率估计概率”的实验时,根据统计结果,绘制了如图所示的折线统计图,则符合这一结果的实验最有可能的是( ) A、抛掷一枚硬币,落地后硬币正面朝上 B、一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正方体骰子,朝上的面点数是3 D、在“石头、剪刀、布”的游戏中,小刚随机出的是“石头”26. 苗圃技术人员对某种花苗移植的成活情况进行调查,将调查数据整理后结果如表所示:
A、抛掷一枚硬币,落地后硬币正面朝上 B、一副去掉大小王的扑克牌,洗匀后,从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正方体骰子,朝上的面点数是3 D、在“石头、剪刀、布”的游戏中,小刚随机出的是“石头”26. 苗圃技术人员对某种花苗移植的成活情况进行调查,将调查数据整理后结果如表所示:移植总数
成活数
成活的频率
根据表中数据,估计这种花苗移植的成活概率为精确到
27. 如图是一枚图钉被抛起后钉尖触地频率随抛掷次数变化趋势图,则一枚图钉被抛起后钉尖触地的概率估计值是 . 28. 如图,某试验小组做了转动转盘,当转盘停止转动后,“指针落在灰色区域内”的试验,试验数据如下表:
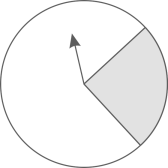
28. 如图,某试验小组做了转动转盘,当转盘停止转动后,“指针落在灰色区域内”的试验,试验数据如下表:试验次数
20
40
60
80
100
1000
“指针落在灰色区域内”的次数
6
11
15
21
25
250
“指针落在灰色区域内”的频率
0.3
0.275
0.25
0.2625
0.25
0.25
根据表格,可以估计出转动转盘一次,当转盘停止转动后,“指针落在灰色区域内”的概率是 . (精确到百分位)
 29. 某种油菜籽在相同条件下的发芽试验的结果如下:
29. 某种油菜籽在相同条件下的发芽试验的结果如下:试验的粒数n
20
80
100
200
400
800
1000
1500
发芽的粒数m
14
54
67
132
264
532
670
1000
发芽的频率
0.7
0.675
0.67
0.66
0.66
0.665
a
0.667
(1)、填空:上表中a=;(2)、根据上表,请估计,当n很大时,发芽的频率将会接近多少?(结果保留两位小数)(3)、根据上表,这种油菜籽发芽的概率的估计值是多少?(结果保留两位小数)30. 某商场设立了一个可以自由转动的转盘(如图所示),并规定:顾客购买 元以上的商品就能获得一次转动转盘的机会,当转盘停止时,指针落在哪个区域就可以获得相应的奖品.如表所示是活动进行中的一组数据:转动转盘的次数
100
150
200
500
800
1000
落在“铅笔”区域的次数
68
111
136
345
564
701
落在“铅笔”区域的频率
_______
_______
_______
_______
_______
_______
 (1)、计算并完成表格:(2)、请估计 很大时,频率将会接近多少?(3)、假如你去转动转盘一次,你获得洗衣粉的概率大约是多少?(4)、在该转盘中,标有铅笔区域的扇形圆心角大约是多少?(精确到 )31. 一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是年平的 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
(1)、计算并完成表格:(2)、请估计 很大时,频率将会接近多少?(3)、假如你去转动转盘一次,你获得洗衣粉的概率大约是多少?(4)、在该转盘中,标有铅笔区域的扇形圆心角大约是多少?(精确到 )31. 一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是年平的 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上频数
14
38
47
52
66
78
88
相应频率
(1)、请将数据补充完整;(2)、画出“兵”字面朝上的频率分布折线图; (3)、如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?
(3)、如果实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?