命题新趋势3 真实情境（1）——2024年北师大版数学七（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、整数的乘除

1. 甲型流感病毒的直径是 $0.00000008 m$ ，将 $0.00000008$ 用科学记数法表示是（）

A、 $0.8 \times 1 0^{- 8}$ B、 $0.8 \times 1 0^{- 7}$ C、 $8 \times 1 0^{- 8}$ D、 $8 \times 1 0^{- 7}$

查看试题解析
2. 蓝山县某中学在课堂探究中，数学老师在边长为 $a$ 的正方形中挖去一个边长为 $b$ 的小正方形（ $a > b$ ）（如图甲），把余下的部分拼成一个矩形（如图乙），根据两个图形中阴影部分的面积相等，同学们可以验证等式（）

A、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ B、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ C、 $a^{2} - b^{2} = (a + b) (a - b)$ D、 $(a + 2 b) (a - 2 b) = a^{2} - a b - 2 b^{2}$

查看试题解析
3. 夏夏在检查作业时，发现有一道题的部分内容被墨水侵染了， $\times \frac{2}{3} a b = 2 a^{2} b^{3} + \frac{1}{3} a^{3} b^{2}$ ，那么这部分内容可能是（）

A、 $(3 a b^{2} + 2 a^{2} b)$ B、 $(3 a^{2} b + \frac{1}{2} a b^{2})$ C、 $(3 a b^{2} + \frac{1}{2} a^{2} b)$ D、 $(\frac{1}{3} a^{2} b^{2} + \frac{1}{2} a^{2} b)$

查看试题解析
4. 今天数学课上，老师讲了单项式乘以多项式，放学回到家，小明拿出课堂笔记本复习，发现一道题：-3xy(4y-2x-1)=-12xy²+6x²y+□，□的地方被墨水弄污了，你认为□处应填写.

查看试题解析
5. 一个老人非常喜欢孩子，每当有孩子到他家做客时，老人都要拿出糖果招待他们．如果来1个孩子，老人就给孩子1块糖果；来2个孩子，老人就给每个孩子2块糖果；如果来3个孩子，老人就给每个孩子3块糖果；……，．有一天， $x$ 个孩子一起去看老人，第二天，有 $y$ 个孩子一起去看老人，第三天 $(x + y)$ 个孩子一起去看老人，那么，第三天老人给出去的糖果比前两天给出去的糖果多块.

查看试题解析
6. 如图，用一段长为 $60 m$ 的篱笆围成一个一边靠墙（墙的长度不限）的长方形菜园 $A B C D$ ，设与墙平行的篱笆 $A B$ 的长为 $x m$ ，菜园的面积为 $y m^{2}$ ．试写出 $y$ 与 $x$ 之间的关系式．

查看试题解析
7. 如图，正方形纸板 $A$ 的边长为 $a$ ，正方形纸板 $B$ 的边长为 $b$ ，用一块纸板 $A$ 、一块纸板 $B$ 和两块长方形纸板 $C$ 可以拼成一个大正方形．

(1)、图2大正方形的边长为；由图1到图2，可以得到一个关于 $a 、 b$ 的等式，直接写出这个等式：；

(2)、利用这个等式解决如下问题：长方形纸板 $C$ 的周长为12，正方形 $A$ 和正方形 $B$ 的面积之和为26，求长方形纸板 $C$ 的面积．

查看试题解析
8. 小聪在做题目 “当 $x = - \frac{1}{2024}$ 时，求代数式 $2 x (x - 1) - (x + 1) (2 x - 4)$ 的值”时，发现：无论 $x$ 取何值，此代数式的值都等于 4 ，你认为小聪的发现正确吗？说说你的理由．

查看试题解析

9. 阅读下列素材，完成相应的任务.

	平衡多项式
素材一：	定义：对于一组多项式： $x + a$ ， $x + b$ ， $x + c$ ( $a$ ， $b$ ， $c$ 都是非零常数），当其中一个多项式的平方与另外两个多项式的乘积的差是一个常数 $m$ 时，称这样的三个多项式是一组平衡多项式， $m$ 的值是这组平衡多项式的平衡因子.
素材二：	例如：对于多项式 $x + 1$ ， $x + 2$ ， $x + 3$ ，因为 ${(x + 2)}_{}^{2} - (x + 1) (x + 3)$ = $x_{}^{2} + 4 x + 4$ $- (x_{}^{2} + 4 x + 3)$ $= 1$ ，所以多项式 $x + 1$ ， $x + 2$ ， $x + 3$ 是一组平衡多项式，其平衡因子为1.
任务一：	小明发现多项式 $x + 3$ ， $x + 5$ ， $x + 7$ 是一组平衡多项式，在求其平衡因子时，列式如下： ${(x + 5)}_{}^{2} - (x + 3) (x + 7)$ ，根据他的思路求该组平衡多项式的平衡因子.
任务二：	判断多项式 $x - 2$ ， $x + 1$ ， $x + 4$ 是否为一组平衡多项式，若是，求出其平衡因子；若不是，说明理由.
任务三：	若多项式 $x - 2$ ， $x + 2$ ， $x + p$ ( $p$ 为非零常数）是一组平衡多项式，求 $p$ 的值.

查看试题解析

10. 【阅读材料】我们知道，图形也是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数量关系，而运用代数思想也能巧妙地解决些图形问题.
在一次数学活动课上，张老师准备了若干张如图1所示的甲、乙、丙三种纸片，其中甲种纸片是边长为x的正方形，乙种纸片是边长为y的正方形，丙种纸片是长为y ，宽为x的长方形.并用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成了如图2所示的一个大正方形.

(1)、【理解应用】
观察图2，用两种不同方式表示阴影部分的面积可得到一个等式，请你直接写出这个等式.

(2)、【拓展升华】
利用（1）中的等式解决下列问题.
①已知 $a^{2} + b^{2} = 10$ ， $a + b = 6$ ，求 $a b$ 的值；
②已知 $(2021 - c) (c - 2019) = - 2020$ ，求 ${(2021 - c)}^{2} + {(c - 2019)}^{2}$ 的值.

查看试题解析

二、相交线与平行线

11. 泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家，据说“两条直线相交，对顶角相等”就是泰勒斯首次发现并论证的．论证“对顶角相等”使用的依据是（　　）

A、等角的补角相等 B、同角的余角相等 C、等角的余角相等 D、同角的补角相等

查看试题解析
12. 如图，已知 $∠ 1 = 90 °$ ，为保证两条铁轨平行，添加的下列条件中，正确的是（）

A、 $∠ 2 = 90 °$ B、 $∠ 3 = 90 °$ C、 $∠ 4 = 90 °$ D、 $∠ 5 = 90 °$

查看试题解析
13. 如图，一把长方形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=125°，则∠DBC的度数为（）

A、55° B、65° C、75° D、125°

查看试题解析
14. 如图，现要从村庄P修建一条连接公路AB的最短小路，过点P作 $P C ⊥ A B$ 于点C，沿PC修建公路就能满足小路最短，这样做的依据是．

查看试题解析
15. 如图，平原上有A，B，C，D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池．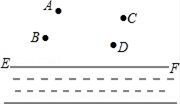

(1)、不考虑其他因素，请你画图确定蓄水池H点的位置，使它到四个村庄距离之和最小；

(2)、计划把河水引入蓄水池H中，怎样开渠最短并说明根据．

查看试题解析
16. 【探究学习】小学阶段，我们可以通过“拼”角、“折”角，观察得到三角形内角和为180°．现在我们学习了平行线的性质，就可以证明此结论的正确性了．

(1)、如图1，过 $△ A B C$ 的顶点A作BC的平行线ED ，请你证明三角形的内角和为180°；
【解题反思】平行线具有“等角转化”的功能．

(2)、【迁移应用】健康骑行越来越受到老百姓的喜欢，自行车的示意图如图2，其中 $A B ∥ C D$ ．
①若 $∠ E A B = 60 °$ ， $∠ E C D = 40 °$ ，则 $∠ A E C$ 的度数为_▲_；
②若 $A E ∥ B D$ ， $∠ A E C = 80 °$ ，求 $∠ A B D - ∠ E C D$ 的度数．

(3)、如图3，若 $A B ∥ C D$ ，点P在AB ， CD外部，请直接写出 $∠ B$ ， $∠ D$ ， $∠ B P D$ 之间的关系．

查看试题解析

三、变量之间的关系

17. 如图，折线OEFPMN描述了某汽车在行驶过程中速度与时间的关系，下列说法中错误的是（）

A、第9分钟时汽车的速度是60千米/时 B、从第3分钟到第6分钟，汽车停止 C、从第9分钟到第12分钟，汽车的速度逐渐减小 D、第12分钟时汽车的速度是0千米/时

查看试题解析
18. 一种手持烟花，这种烟花每隔0.5秒发射一发花弹，每一发花弹的飞行路径，爆炸时的高度均相同.皮皮小朋友发射出的第一发花弹的飞行高度h（米）随飞行时间t（秒）变化的规律如下表所示.下列对这一变化的过程说法正确的是（）
t/秒
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
…
h/米
1.8
7.3
11.8
15.3
17.8
19.3
19.8
19.3
17.8
15.3
…

A、飞行时间t每增加0.5秒，飞行高度h就增加5.5米 B、飞行时间t每增加0.5秒，飞行高度h就减少5.5米 C、估计飞行时间t为5秒时，飞行高度h为11.8米 D、从0秒到2秒花弹飞行的高度是15米

查看试题解析
19. 谚语“冰冻三尺非一日之寒”体现了冰的厚度随时间变化的一个变化过程，在该变化过程中因变量是．

查看试题解析

20. 王勇买了一张

30

元的租书卡，每租一本书后卡中剩余金额

y

（元）与租书本数

x

（本）之间的关系式为.

租书数 $/$ 本	卡中余额 $/$ 元
$1$	$30 - 0.8$
$2$	$30 - 1.6$
$3$	$30 - 2.4$
……	……

查看试题解析

21. 某商店为了减少某种商品的积压，采取降价销售的策略．某商品原价为520元/件，随着不同幅度的降价，每降价10元，日销量增加5件．该商品降价x（元）与日销量y（件）之间的关系如下表：

降价x/元	0	10	20	30	40	50	60
日销量y/件	150	155	160	165	b	175	180

(1)、上表中的自变量是什么？因变量是什么？

(2)、求表中b的值；

(3)、若该商品的售价为440元，求该商品的日销量为多少件？

查看试题解析

22. 根据心理学家研究发现，学生对一个新概念的接受能力y与提出概念所用的时间x（分钟）之间有如下关系（其中0≤x≤30）

提出概念所用时间（x）	2	5	7	10	12	13	14	17	20
对概念的接受能力（y）	47.8	53.5	56.3	59	59.8	59.9	59.8	58.3	55

(1)、上表中反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

(2)、根据表格中的数据，提出概念所用时间是多少时，学生的接受能力最强？

(3)、学生对一个新概念的接受能力在什么时间段内逐渐增强？在什么时间段内逐渐减弱？

查看试题解析