命题新趋势3 真实情境(2)——2024年浙教版数学八(下)期末复习
试卷更新日期:2024-06-02 类型:复习试卷
一、平行四边形
-
1. 下列三星堆文物图案中,既是中心对称图形又是轴对称图形( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图案是一些国产新能源车的车标,其中既是轴对称图形又是中心对称图形的是( )A、
2. 下列图案是一些国产新能源车的车标,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、
3. 中国航天取得了举世瞩目的成就,为人类和平贡献了中国智慧和中国力量,下列是有关中国航天的图标,其文字上方的图案是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 以下是四类垃圾分类的标志图案,则四幅标志图案中是中心对称图形的是( )A、
4. 以下是四类垃圾分类的标志图案,则四幅标志图案中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5.
5.如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=50cm,当它的一端B着地时,另一端A离地面的高度AC为( )
 A、25cm B、50cm C、75cm D、100cm6. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.以下是在棋谱中截取的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、
A、25cm B、50cm C、75cm D、100cm6. 围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.以下是在棋谱中截取的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、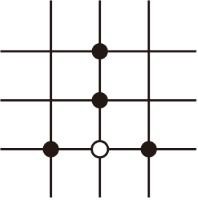 B、
B、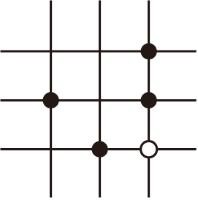 C、
C、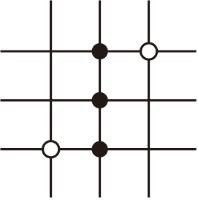 D、
D、 7. 第五套人民币中的5角硬币色泽为镍白色,正,反面的内周边缘均为正十一边形.则其内角和为 °.
7. 第五套人民币中的5角硬币色泽为镍白色,正,反面的内周边缘均为正十一边形.则其内角和为 °. 8. 如图,要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB、AC,并取AB、AC的中点D、E,连结DE.小明测得DE的长为a米,则B、C两地的距离为米.
8. 如图,要测量B,C两地的距离,小明想出一个方法:在池塘外取点A,得到线段AB、AC,并取AB、AC的中点D、E,连结DE.小明测得DE的长为a米,则B、C两地的距离为米. 9. 小明设计了测量池塘两端AB距离的方案,如图,先取一点C,连结AC,BC,再取它们的中点D,E,测得DE=15米,则AB=米.
9. 小明设计了测量池塘两端AB距离的方案,如图,先取一点C,连结AC,BC,再取它们的中点D,E,测得DE=15米,则AB=米. 10. 如图1,DE 是△ABC 的中位线,李琳同学对这个图形进行了剪拼,先连结AD(如图2),再沿 AD剪开(如图3),然后将△ABD置于△ADC的下面,使 BD和CD重合,△ADC与△DCF共面(如图4).李琳同学对剪拼后的图形很感兴趣,于是自编了一道数学题:如图4,在四边形 ADFC 中,DE 是△ADC 的中线,∠DCF=∠DCA+∠DAC,FC=AD.求证
10. 如图1,DE 是△ABC 的中位线,李琳同学对这个图形进行了剪拼,先连结AD(如图2),再沿 AD剪开(如图3),然后将△ABD置于△ADC的下面,使 BD和CD重合,△ADC与△DCF共面(如图4).李琳同学对剪拼后的图形很感兴趣,于是自编了一道数学题:如图4,在四边形 ADFC 中,DE 是△ADC 的中线,∠DCF=∠DCA+∠DAC,FC=AD.求证请你解答李琳自编的题.
 11. 某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程:
11. 某数学活动小组在研究三角形拓展图形的性质时,经历了如下过程: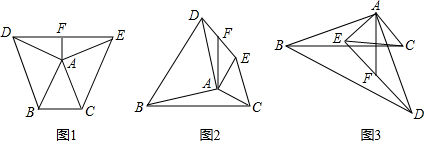 (1)、●操作发现
(1)、●操作发现在等腰△ABC中,AB=AC , 分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图①所示,连接DE , 其中F是DE的中点,连接AF , 则下列结论正确的是(填序号即可)
①AF=BC:②AF⊥BC;③整个图形是轴对称图形;④DE∥BC、
(2)、●数学思考在任意△ABC中,分别以AB和AC为腰,向△ABC的外侧作等腰直角三角形,如图②所示,连接DE , 其中F是DE的中点,连接AF , 则AF和BC有怎样的数量和位置关系?请给出证明过程
(3)、●类比探索在任意△ABC中,仍分别以AB和AC为腰,向△ABC的内侧作等腰直角三角形,如图③所示,连接DE , 其中F是DE的中点,连接AF , 试判断AF和BC的数量和位置关系是否发生改变?并说明理由.
12. 数学活动课上,老师组织数学小组的同学进行以“三角形卡片拼接与变换”为主题的数学学习活动.他们准备若干个 , 的特殊直角三角形卡片,其中在三角形卡片中, , , . (1)、如图1,将一个与全等的沿较长的直角边重合,拼成一个四边形 .
(1)、如图1,将一个与全等的沿较长的直角边重合,拼成一个四边形 .①求证:四边形是平行四边形;
②连接交于点 , 求的面积;
(2)、在(1)的条件下,将一条直角边与重合的等腰直角三角形卡片)与四边形拼成如图2所示的平面图形,请求出点到的距离;(3)、一个斜边长度与相等的三角板( , )如图3摆放,将绕点顺时针旋转,旋转角为 , 旋转后的三角形记为 . 在旋转过程中,直线所在的直线与直线 , 交于 , 两点,当为等腰三角形时,请直接写出的长.二、特殊平行四边形
-
13. 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
 A、①② B、②③ C、①③ D、②④14. 在数学活动课上,老师让同学们判断一个由四根木条组成的四边形是否为矩形,下面是一个学习小组拟定的方案,其中正确的方案是( )A、测量四边形的三个角是否为直角 B、测量四边形的两组对边是否相等 C、测量四边形的对角线是否平分 D、测量四边形的其中一组邻边是否相等15. 如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其推理依据是( )
A、①② B、②③ C、①③ D、②④14. 在数学活动课上,老师让同学们判断一个由四根木条组成的四边形是否为矩形,下面是一个学习小组拟定的方案,其中正确的方案是( )A、测量四边形的三个角是否为直角 B、测量四边形的两组对边是否相等 C、测量四边形的对角线是否平分 D、测量四边形的其中一组邻边是否相等15. 如图,用一根绳子检查一平行四边形书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线AC,BD就可以判断,其推理依据是( ) A、矩形的对角线相等 B、矩形的四个角是直角 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是矩形16. 延时课上,王林用四根长度都为的木条制作了图1所示正方形,而后将正方形的边固定,平推成图的图形,并测得 , 则在此变化过程中结论错误的是( )
A、矩形的对角线相等 B、矩形的四个角是直角 C、对角线相等的四边形是矩形 D、对角线相等的平行四边形是矩形16. 延时课上,王林用四根长度都为的木条制作了图1所示正方形,而后将正方形的边固定,平推成图的图形,并测得 , 则在此变化过程中结论错误的是( ) A、长度不变,为 B、长度变小,减少 C、长度变大,增大 D、面积变小,减少17. 数学老师用四根长度相等的木条首尾顺次相接制成一个如图1所示的菱形教具,此时测得 , 对角线长为 , 改变教具的形状成为如图2所示的正方形,则正方形的边长为( )
A、长度不变,为 B、长度变小,减少 C、长度变大,增大 D、面积变小,减少17. 数学老师用四根长度相等的木条首尾顺次相接制成一个如图1所示的菱形教具,此时测得 , 对角线长为 , 改变教具的形状成为如图2所示的正方形,则正方形的边长为( ) A、 B、 C、 D、18. 如图1为停车场出入口的车辆识别道闸,机箱高8分米,与墙面的距离分米,静止时档杆为长方形.当车辆通行时,档杆升起降下,各边长度保持不变,如图2所示,当档杆升至点恰好与点高度相同时,点到地面的距离为15分米,则分米.当档杆升至离地距离为16分米时,到的距离为到距离的3倍,则分米.
A、 B、 C、 D、18. 如图1为停车场出入口的车辆识别道闸,机箱高8分米,与墙面的距离分米,静止时档杆为长方形.当车辆通行时,档杆升起降下,各边长度保持不变,如图2所示,当档杆升至点恰好与点高度相同时,点到地面的距离为15分米,则分米.当档杆升至离地距离为16分米时,到的距离为到距离的3倍,则分米. 19. 如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度 , 当摆锤摆动到最高位置时,它离底座的垂直高度 , 此时摆锤与静止位置时的水平距离时,钟摆的长度是 .
19. 如图,有一只摆钟,摆锤看作一个点,当摆锤静止时,它离底座的垂直高度 , 当摆锤摆动到最高位置时,它离底座的垂直高度 , 此时摆锤与静止位置时的水平距离时,钟摆的长度是 . 20. 用四根长度相等的木条制作学具,先制作图(1)所示的正方形 , 测得 , 活动学具成图(2)所示的四边形 , 测得 , 则图(2)中BD的长是cm.
20. 用四根长度相等的木条制作学具,先制作图(1)所示的正方形 , 测得 , 活动学具成图(2)所示的四边形 , 测得 , 则图(2)中BD的长是cm. 21. 小林同学是一名剪纸爱好者,喜欢运用数学知识对自己的剪纸作品进行分析思考,下面是他利用勾股定理对部分剪纸作品的数量关系进行探究思考的过程,请你帮助他一起完成.
21. 小林同学是一名剪纸爱好者,喜欢运用数学知识对自己的剪纸作品进行分析思考,下面是他利用勾股定理对部分剪纸作品的数量关系进行探究思考的过程,请你帮助他一起完成. (1)、如图1,图案1是以Rt的三条边为直径,向外作半圆,其面积分别记为 , 请写出之间的数量关系: .(2)、如图2,这是由四个全等的直角三角形紧密地拼接形成的飞镖状图案,测得外围轮廓(实线)的周长为80, , 求该飞镖状图案的面积.(3)、如图3,这是由八个全等的直角三角形紧密地拼接形成的大正方形 , 记图中正方形 , 正方形 , 正方形的面积分别为 . 若 , 则 .22. 如图,菱形花坛的边长为 , , 沿着菱形的对角线修建了两条小路和 , 求两条小路的长和花坛的面积.
(1)、如图1,图案1是以Rt的三条边为直径,向外作半圆,其面积分别记为 , 请写出之间的数量关系: .(2)、如图2,这是由四个全等的直角三角形紧密地拼接形成的飞镖状图案,测得外围轮廓(实线)的周长为80, , 求该飞镖状图案的面积.(3)、如图3,这是由八个全等的直角三角形紧密地拼接形成的大正方形 , 记图中正方形 , 正方形 , 正方形的面积分别为 . 若 , 则 .22. 如图,菱形花坛的边长为 , , 沿着菱形的对角线修建了两条小路和 , 求两条小路的长和花坛的面积. 23. 阅读理解:德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿”.(1)、如图,点把线段分成两部分,如果 , 那么称点为线段的黄金分割点.在图中,若 , 则__________(保留根号).
23. 阅读理解:德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿”.(1)、如图,点把线段分成两部分,如果 , 那么称点为线段的黄金分割点.在图中,若 , 则__________(保留根号). (2)、宽与长的比是(约为)的矩形叫做黄金矩形,黄金矩形给我们以协调.匀称的美感,世界各国许多著名的建筑为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为的矩形纸片折叠黄金矩形.(提示:)
(2)、宽与长的比是(约为)的矩形叫做黄金矩形,黄金矩形给我们以协调.匀称的美感,世界各国许多著名的建筑为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为的矩形纸片折叠黄金矩形.(提示:)第一步 在矩形纸片一端,利用图的方法折出一个正方形,然后把纸片展平.
第二步 如图 , 把这个正方形折成两个相等的矩形,再把纸片展平.
第三步 如图 , 折出内侧矩形的对角线 , 并把折到图中所示的处.
第四步 展平纸片,按所得的点折出 , 使 , 则图④中就出现黄金矩形.
问题解决:

①图中(保留根号);
②请写出图中所有的黄金矩形: , 并证明;
③请结合图 , 在矩形中添加一条线段,设计一个新的黄金矩形,用字母表示出来,并证明.
24. 在数学活动课上,老师出了一道关于矩形的题,让同学们解答.如图所示,在菱形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,且AF=CE,连接BD,DF.求证:四边形BFDE是矩形

嘉嘉和琪琪分别给出了自己的思路:
嘉嘉:先证明四边形BFDE是平行四边形,然后利用矩形定义即可
得证;
琪琪:先证明△ADF与△CBE全等,然后利用“有三个角是直角的四边形是矩形”即可得证
(1)、嘉嘉的思路 , 琪琪的思路;(均选填“正确”或“错误”)(2)、请按照你认为的正确思路进行解答.25. 探索与发现小李同学在用作图软件探索图形性质的数学活动中,进行如下操作:
如图,在边长为3的正方形ABCD的AB边上取定点E , 使AE=1,在AD边上设置动点P , 连接PE , 以PE为边在AB的上方作正方形PEFG , 接AF , BF .
 (1)、小李同学通过观察发现图中∠APE=∠FEB , 请给出证明;(2)、探索过程中发现,在点P运动过程中,△AFB的面积是个定值,请证明并求出这个定值 ;(3)、进一步探索后发现,随着点P的运动,△AFB的周长会随点P位置的变化而变化,但存在一个最小值,请你求出△AFB周长的最小值.26. 综合与探究
(1)、小李同学通过观察发现图中∠APE=∠FEB , 请给出证明;(2)、探索过程中发现,在点P运动过程中,△AFB的面积是个定值,请证明并求出这个定值 ;(3)、进一步探索后发现,随着点P的运动,△AFB的周长会随点P位置的变化而变化,但存在一个最小值,请你求出△AFB周长的最小值.26. 综合与探究折纸是一种艺术,其中也包含了高超的技术,数学折纸活动有益于开发智力,拓展思维,在折纸活动中体会数学知识的内涵,理解数学知识的应用,可以让我们感悟到严谨的数学之美,八(4)班数学兴趣小组的同学们在活动课进行了折纸问题探究.

【方法提示】
数学折纸问题的解决通常结合轴对称和全等的相关知识性质,要关注折叠前后对应的边和对应的角等一些不变的关系.
【动手操作】
如图,将一张矩形纸片沿长边进行折叠(已知),使点落在边上,折痕为(点在边上,点在边上),折叠后点 , 的对应点分别为点 , .
【问题探究】
(1)、判断图中四边形的形状,并证明你的结论.(2)、随着点落在不同的位置,折痕位置也在变化,若矩形纸片中 , , 求线段长度的取值范围.27. 综合与实践:问题情境:数学课上,小广和小都两位同学利用三角板操作探究图形的旋转问题.
 (1)、操作探究:小广将两块全等的含角的直角三角板按如图①方式在平面内放置,其中两锐角顶点重合于点 , , 已知长 , 则点、之间的距离为 .(2)、操作探究:小都将两块全等的含角的直角三角板按如图②方式在平面内放置.
(1)、操作探究:小广将两块全等的含角的直角三角板按如图①方式在平面内放置,其中两锐角顶点重合于点 , , 已知长 , 则点、之间的距离为 .(2)、操作探究:小都将两块全等的含角的直角三角板按如图②方式在平面内放置.其中两个角顶点重合于点 , 与重合,已知长 , 请你帮小都同学求出此时点、之间的距离;
(3)、操作探究:随后,小将图②中的换成了含角的三角板,同相是顶点重合于点 , 与重合,已知直角边与长均为 , 他还想求点 , 之间距离,小广提出,如果把三角板也换成了含角的三角板,并利用旋转的知识,结论将更容易得到,你能求出此时点 , 之间的距离吗?三、反比例函数
-
28. 为了预防流感,某中学用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分)成正比例,药物释放完毕后,y与x成反比例,整个过程中y关于x的函数图象如图所示.据测定,当空气中每立方米的含药量降低到0.45毫克以下时,学生方可进入教室,则从药物释放完毕到学生能够进入教室,至少要经过( )
 A、4.2小时 B、B.4小时 C、3.8小时 D、D.3.5小时29. 为预防春季流感,学校对教室进行喷雾消毒,喷雾阶段教室内每立方米空气中含药量y(mg)与时间x(min)成正比例,喷雾完成后y与x成反比例,其函数关系图象如图所示,已知当每立方米空气中含药量低于 1.6m g时,对人体方能无毒害作用,则下列说法正确的是 ( )
A、4.2小时 B、B.4小时 C、3.8小时 D、D.3.5小时29. 为预防春季流感,学校对教室进行喷雾消毒,喷雾阶段教室内每立方米空气中含药量y(mg)与时间x(min)成正比例,喷雾完成后y与x成反比例,其函数关系图象如图所示,已知当每立方米空气中含药量低于 1.6m g时,对人体方能无毒害作用,则下列说法正确的是 ( ) A、每立方米空气中含药量从6mg上升到8mg需要2min B、每立方米空气中含药量下降的过程中,y关于x 的函数表达式为 C、为了确保对人体无毒害作用,喷雾完成25 min 后学生才能进入教室 D、每立方米空气中含药量不低于4m g的持续时间为7.5min30. 已知蓄电池的电压为定值,使用蓄电池时,电流I(A)与电阻 R(Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流为不能超过6 A,那么用电器的可变电阻R 应控制在 ( )
A、每立方米空气中含药量从6mg上升到8mg需要2min B、每立方米空气中含药量下降的过程中,y关于x 的函数表达式为 C、为了确保对人体无毒害作用,喷雾完成25 min 后学生才能进入教室 D、每立方米空气中含药量不低于4m g的持续时间为7.5min30. 已知蓄电池的电压为定值,使用蓄电池时,电流I(A)与电阻 R(Ω)是反比例函数关系,它的图象如图所示.如果以此蓄电池为电源的用电器的限制电流为不能超过6 A,那么用电器的可变电阻R 应控制在 ( ) A、R≥2Ω B、0Ω<R≤2Ω C、R≥1Ω D、0Ω<R≤1Ω31. 近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近视眼镜,则镜片焦距x(米)的取值范围是( )
A、R≥2Ω B、0Ω<R≤2Ω C、R≥1Ω D、0Ω<R≤1Ω31. 近视眼镜的度数y(度)与镜片焦距x(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近视眼镜,则镜片焦距x(米)的取值范围是( )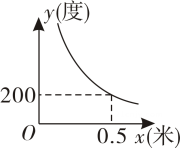 A、0<x<0.25 B、x>0.25 C、0<x<0.2 D、x>0.232. 王华和王强同学在合作电学实验时,记录下电流 (A)与电阻 有如下对应关系.观察下表.
A、0<x<0.25 B、x>0.25 C、0<x<0.2 D、x>0.232. 王华和王强同学在合作电学实验时,记录下电流 (A)与电阻 有如下对应关系.观察下表.R
…
2
4
8
10
16
…
…
16
8
4
3.2
2
…
你认为 与 间的函数关系式为;当电阻 时,电流 A.
33. 油箱注满 升油后,轿车可行驶的总路程 (单位:千米)与平均耗油量 (单位:升/千米)之间是反比例函数关系 ( 是常数, .已知某轿车油箱注满油后,以平均耗油量为每千米0.1升的速度行驶,可行驶700千米.则该轿车可行驶的总路程 与平均耗油量 之间的函数关系式为.34. 一辆汽车前灯电路上的电压U(V)保持不变,通过灯泡的电流强度I(A)是电阻R(Ω)的反比例函数.若当电阻为30Ω时,通过灯泡的电流强度为0.40A,则当电阻为50Ω时,通过灯泡的电流强度为 A.35. 要制作一种糖质工艺品,需先把材料加热到才能进行操作.设材料的温度为 , 从加热开始计算的时间为 . 该材料在加热时,温度与时间的函数关系图象是一次函数图象的一部分;停止加热后,温度与时间的函数关系图象是反比例函数图象的一部分.已知该材料加热前的温度是 , 加热时温度达到 . (1)、分别求出材料加热过程中及停止加热后,关于的函数表达式.(2)、为节约能源,加工时采用间歇加热法,即把材料加热到后停止加热,等温度降至时,再次加热到后停止加热.那么从第一次加热至可以操作到第二次再需加热,整个过程可操作的时间有多长?36. 五一假期,小王一家从杭州到温州自驾游,已知杭州到温州市区A处的路程为300千米,小王家的车油箱的容积为55升,小王把油箱加满后驾驶汽车从杭州出发.(1)、求汽车行驶的总路程s(单位:千米)与平均耗油量b(单位:升/千米)的函数表达式.(2)、小王以平均每千米耗油0.1升的速度驾驶汽车到达温州市区A处,休整后沿图示路线继续出发,先到雁荡山B处,再到楠溪江C处,最后到洞头D处.由于下雨,从A处开始直到D处小王降低了车速,此时平均每千米的耗油量增加了20%.如果小王始终以此速度行驶,不需加油能否到达洞头D处?如果不能,至少还需加多少油?
(1)、分别求出材料加热过程中及停止加热后,关于的函数表达式.(2)、为节约能源,加工时采用间歇加热法,即把材料加热到后停止加热,等温度降至时,再次加热到后停止加热.那么从第一次加热至可以操作到第二次再需加热,整个过程可操作的时间有多长?36. 五一假期,小王一家从杭州到温州自驾游,已知杭州到温州市区A处的路程为300千米,小王家的车油箱的容积为55升,小王把油箱加满后驾驶汽车从杭州出发.(1)、求汽车行驶的总路程s(单位:千米)与平均耗油量b(单位:升/千米)的函数表达式.(2)、小王以平均每千米耗油0.1升的速度驾驶汽车到达温州市区A处,休整后沿图示路线继续出发,先到雁荡山B处,再到楠溪江C处,最后到洞头D处.由于下雨,从A处开始直到D处小王降低了车速,此时平均每千米的耗油量增加了20%.如果小王始终以此速度行驶,不需加油能否到达洞头D处?如果不能,至少还需加多少油? 37. 已知,视力表上视力值和字母的宽度(mm)之间的关系是我们已经学过的一类函数模型,字母的宽度如图1所示,经整理,视力表上部分视力值和字母的宽度(mm)的对应数据如表所示:
37. 已知,视力表上视力值和字母的宽度(mm)之间的关系是我们已经学过的一类函数模型,字母的宽度如图1所示,经整理,视力表上部分视力值和字母的宽度(mm)的对应数据如表所示:位置
视力值
的值(mm)
第1行
0.1
70
第5行
0.25
28
第8行
0.5
14
第14行
2.0
3.5
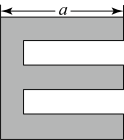 (1)、请你根据表格数据判断并求出视力值和字母的宽度(mm)之间的函数表达式,并说明理由;(2)、经过测量,第4行和第7行两行首个字母E的宽度a(mm)的值分别是35mm和17.5mm,求第4行、第7行的视力值.38. 为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为 .
(1)、请你根据表格数据判断并求出视力值和字母的宽度(mm)之间的函数表达式,并说明理由;(2)、经过测量,第4行和第7行两行首个字母E的宽度a(mm)的值分别是35mm和17.5mm,求第4行、第7行的视力值.38. 为预防传染病,某校定期对教室进行“药熏消毒”.已知某种药物在燃烧阶段,室内每立方米空气中的含药量与燃烧时间成正比例;一次性燃烧完以后,y与x成反比例(如图所示).在药物燃烧阶段,实验测得在燃烧5分钟后,此时教室内每立方米空气含药量为 . (1)、若一次性燃烧完药物需10分钟.
(1)、若一次性燃烧完药物需10分钟.①分别求出药物燃烧时及一次性燃烧完以后y关于x的函数表达式.
②当每立方米空气中的含药量低于时,对人体方能无毒害作用,那么从消毒开始,在哪个时间段学生不能停留在教室里?
(2)、已知室内每立方米空气中的含药量不低于时,才能有效消毒,如果有效消毒时间要持续120分钟,问要一次性燃烧完这种药物需多长时间?39. 电灭蚊器的电阻y(kΩ)随温度x(℃)变化的大致图象如图所示,通电后温度由室温10℃上升到30℃时,电阻与温度成反比例函数关系,且在温度达到30℃时,电阻下降到最小值,随后电阻随温度升高而增加,温度每上升1℃,电阻增加kΩ.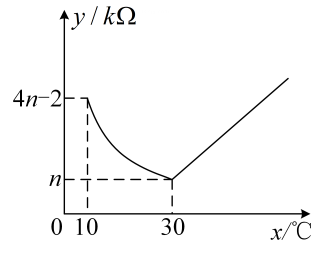 (1)、当10≤x≤30时,求y与x之间的关系式;(2)、电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5kΩ?
(1)、当10≤x≤30时,求y与x之间的关系式;(2)、电灭蚊器在使用过程中,温度x在什么范围内时,电阻不超过5kΩ?