命题新趋势3 真实情境（3）——2024年浙教版数学七（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、分式

1. 某帐篷生产企业承接生产7000顶帐篷的任务，原计划每天生产x顶，但后因帐篷急需，该企业加大生产投入，提高生产效率，实际每天生产数量提高到原计划的1.4倍，结果提前4天完成任务．根据题意，下面所列方程正确的是（）

A、 $\frac{7000}{x} - \frac{7000}{1.4 x + x} = 4$ B、 $\frac{7000}{x} = \frac{7000}{1.4 x} - 4$ C、 $\frac{7000}{x + 1.4 x} - \frac{7000}{x} = 4$ D、 $\frac{7000}{x} - \frac{7000}{1.4 x} = 4$

查看试题解析

2. 阅读以下内容，完成问题．

解： $1 - \frac{x - y}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 x y + 4 y^{2}}$

$= \frac{x + 2 y - (x - y)}{x + 2 y} \div \frac{(x + y) (x - y)}{(x + 2 y) (x + 2 y)}$ ①

$= \frac{y}{x + 2 y} \cdot \frac{(x + 2 y) (x + 2 y)}{(x + y) (x - y)}$ ②

$= \frac{y (x + 2 y)}{(x + y) (x - y)}$ ③

$= \frac{x y + 2 y^{2}}{x^{2} - y^{2}}$ ④

(1)、小明的计算步骤中，从哪一步开始出现错误？（填写序号）

(2)、小明从第①步的运算结果到第②步的运算是否正确？（填“是”或“否”）若不正确，错误的原因是．

(3)、请你帮小明写出此题完整正确的解答过程．

查看试题解析

3. 某超市同时卖出了一个“宸宸”和一个“莲莲”吉祥物玩偶，售价均为90元，按成本计算，营业员发现“宸宸”盈利了50%，而“莲莲”却亏损了40%，则超市共（）

A、不盈利也不亏损 B、盈利30元 C、亏损30元 D、盈利10元

查看试题解析
4. 现在5G手机非常流行，5G比4G下载速度每秒多120MB，下载一部900MB的电影，5G比4G要快200秒，那么5G手机的下载速度是多少呢?若设5G手机的下载速度为xMB/秒，则根据题意可列方程为（）

A、 $\frac{900}{x} - \frac{900}{x - 120} = 200$ B、 $\frac{900}{x - 120} - \frac{900}{x} = 200$ C、 $\frac{900}{x + 120} + \frac{900}{x} = 200$ D、 $\frac{900}{x} + 200 = \frac{900}{x + 120}$

查看试题解析
5. 有一个容积为24 m³的圆柱形的空油罐，用一根细油管向油罐内注油，当注油量达到该油罐容积的一半时，改用一根口径为细油管口径2倍的粗油管向油罐注油，直至注满，注满油的全过程共用30分钟，求细油管的注油速度.设细油管的注油速度为每分钟x(m³)，根据题意列方程正确的是（）

A、 $\frac{12}{x} + \frac{12}{4 x} = 30$ B、 $\frac{15}{x} + \frac{15}{4 x} = 24$ C、 $\frac{30}{x} + \frac{30}{2 x} = 24$ D、 $\frac{12}{x} + \frac{12}{2 x} = 30$

查看试题解析
6. 甜瓜是某地的特色时令水果.甜瓜一上市，水果店的小李就用3000元购进了一批，前两天以高于进价40%的价格共卖出150kg，第三天她发现市场上甜瓜数量陡增，而自己的甜瓜卖相已不太好，于是果断地将剩余甜瓜以低于进价20%的价格全部售出，前后一共获利 750元，则小李购进甜瓜的质量为（）

A、180 kg B、200 kg C、240 kg D、300 kg

查看试题解析
7. 小明家购进一台扫拖一体机器人．该机器人识别出小明家需要扫地和拖地的面积均为 $60 m^{2}$ ，小明让机器人对识别的面积先扫地再拖地，发现拖地的时间比扫地的时间多 $100 m i n$ ，且扫地的速度是拖地的 3 倍．若拖地的速度为 $x m^{2} / m i n$ ，则可列方程为

查看试题解析
8. 一房屋设计图原房间窗户面积为3m² ，地面面积为18m² ，该住户要求把房间的窗户和地面都增加相同的整数面积（单位：m²）的方式加强采光效果，并使窗户面积与地面面积的比值尽可能接近 $\frac{1}{3}$ ，则增加的面积为m² ．

查看试题解析
9. 为了改善生态环境，防治水土流失，某村计划在荒坡上种植 480 棵树．由于青年志愿者的加入，每日比原计划多种 $\frac{1}{3}$ ，结果提前 4 天完成任务．设志愿者加入后每天种树 $x$ 棵，则所列方程为

查看试题解析
10. 某校学生为受灾地区捐款.已知第一次捐款总额为4800元，第二次捐款总额为 5000元，第二次捐款人数比第一次多20人，两次人均捐款额恰好相等.如果设第一次捐款人数为x人，则第二次捐款人数为人，第一次人均捐款额用关于x的代数式可表示为 $\frac{4800}{x}$ 元，第二次人均捐款额用关于x 的代数式可表示为元，根据两次人均捐款额相等，可列出方程.

查看试题解析
11. 某工厂承接了一项纸箱加工任务，用如图 1 所示的长方形和正方形纸板 (长方形的宽与正方形的边长相等)作侧面和底面，加工成如图 2 所示的坚式和横式两种无盖的长方体纸箱(加工时接缝材料不计)．

(1)、若该厂仓库里有 100 张正方形纸板和 200 张长方形纸板．问坚式和横式纸箱各加工多少个，恰好将库存的两种纸板全部用完？

(2)、该工厂原计划用若干天加工纸箱 200 个，后来由于对方急需要货，实际加工时每天加工速度是原计划的 1.5 倍，这样提前 2 天超额完成了任务，且总共比原计划多加工 40 个，问原计划每天加工纸箱多少个？

查看试题解析
12. 第 19 届亚洲运动会于 2023 年 9 月 23 日至 10 月 8 日在杭州举行，杭州奥体中心体育场成为杭州 2023 年亚运会的主场馆之一．某工厂承包了主场馆建设中某一零件的生产任务，需要在规定时间内生产 24000 个零件，若每天比原计划多生产 30 个零件，则在规定时间内可以多生产 300 个零件．

(1)、求原计划每天生产的零件个数和规定的天数．

(2)、为了提前完成生产任务，工厂在安排原有工人按原计划正常生产的同时，引进 5 组机器人生产流水线共同参与零件生产，已知每组机器人生产流水线每天生产零件的个数比 20 个工人原计划每天生产的零件总数还多 $20 %$ ，按此测算，可恰好提前两天完成 24000 个零件的生产任务，求原计划安排的工人人数．

查看试题解析
13. [问题提出]
我们在分析解决某些数学问题时，经常要比较两个数或代数式的大小，而解决问题的策略一般要进行一定的转化，其中“作差法”就是常用的方法之一，所谓“作差法”，就是通过作差、变形，并利用差的符号确定两个数或代数式的大小，即要比较代数式M，N的大小，只要作出它们的差M-N，若M-N>0，则M>N；若M-N=0，则M=N；若M-N<0，则M<N．
[问题解决]
如图1所示，把边长为a+b(a≠b)的大正方形分割成两个边长分别是a， b的小正方形及两个矩形，试比较两个小正方形面积之和M与两个矩形面积之和N的大小．
由图可知M=a²+b² ， N=2ab．
所以M-N=a²+b²-2ab=(a-b)² ．
因为a≠b，所以(a-b)²>0．
所以M-N>0，所以M>N．

(1)、[类比应用]
Ⅰ.已知小丽和小颖购买同一种商品的平均价格分别为 $\frac{a + b}{2}$ 元/千克和 $\frac{2 a b}{a + b}$ 元/千克(a，b是正数，且a≠b)，试比较小丽和小颖所购买商品的平均价格的高低．
Ⅱ.试比较图2和图3中两个矩形的周长M₁ ， N₁的大小(b>c) ．

(2)、[联系拓广]
小刚在超市里买了一些物品，用一个长方体的箱子“打包”，这个箱子的尺寸如图4所示(其中b>a>c>0)，售货员分别可按图5、图6、图7中的三种方法进行捆绑，问哪种方法用绳最短？哪种方法用绳最长？请说明理由．

查看试题解析
14. 如图， $A$ 种小麦试验田是边长为 $a$ 的正方形中减去一个边长为 $b$ 的正方形蓄水池后余下的部分； $B$ 种小麦试验田是边长为 $\frac{1}{2} (a + b)$ 的正方形.

(1)、设两块试验田都收获了 $m (kg)$ 小麦，求 $A$ ， $B$ 两种小麦单位面积产量的比.

(2)、当 $a = 2 b$ 时， $A$ ， $B$ 两种小麦单位面积产量哪个较大？

(3)、若 $A$ ， $B$ 两种小麦单位面积产量相同，求 $a$ ， $b$ 满足的关系式.

查看试题解析
15. 本月我市进入梅雨季节，为了保障居民的生命财产安全，某社区购进A，B两种型号的抽水泵共100台，A型抽水泵1000元/台，B型抽水泵1500元/台，购进两种型号抽水泵共用130000元．

(1)、求该社区购进A，B两种型号的抽水泵各多少台？

(2)、在相同环境下，经厂家测试B型抽水泵每小时的抽水量比A型抽水泵多 $100 m^{3}$ ， A型抽水泵抽水 $2000 m^{3}$ 与B型抽水泵抽水 $2500 m^{3}$ 所需时间相同，求A，B两种型号的抽水泵每小时的抽水量各多少立方米？

查看试题解析
16. 如图是绍兴市“十运会”的吉祥物“越宝、剡娃”，嵊州市甲、乙两工厂接到组委会通知，共同生产这两个吉祥物5万对，已知甲厂每天比乙厂多生产100对吉祥物，且甲厂生产5000对吉祥物所用的时间与乙厂生产4000对吉祥物所用的时间相同．

(1)、求甲、乙两厂每天各生产多少对吉祥物？

(2)、已知甲、乙两厂每天生产这种吉祥物的原料成本分别是4000元和3600元，两厂一起生产这5万对吉祥物，原料成本共为42万元．那么甲、乙两厂分别生产多少天？

查看试题解析
17. 某商铺准备在端午节前购进一批肉粽和蜜枣粽，已知肉粽的单价比蜜枣粽的单价多2.5元，且花300元购买的肉粽数刚好是花100元购买的蜜枣粽数的2倍.

(1)、求肉粽和蜜枣粽的单价分别是多少元？

(2)、若该商铺一次性购进100个蜜枣粽和200个肉粽，并分别以6元/个和10元/个的定价按以下方式销售：端午节前肉粽涨价10%，端午节后肉粽打九折，蜜枣粽的售价始终保持不变.若两种粽子全部售出后共获利570元，求端午节前肉粽售出的个数.

查看试题解析
18. 老师设计了接力游戏，用合作的方式完成分式化简，规则是：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成化简. 过程如图所示：

(1)、接力中，自己负责的一步出现错误的同学是；

(2)、请你书写正确的化简过程，并在“-1，0，1”中选择一个合适的数代入求值.

查看试题解析

19. 在某校的压花拓展课上，甲、乙两位同学每小时能共做 7 幅作品

A

，甲、乙同时开始制作，当甲做了 28 幅作品 A 时，乙做了 21 幅作品 A．

(1)、求甲、乙每小时各做多少幅作品 A．

(2)、学校组织义拍资助西部贫困学生的活动，甲、乙两位同学计划共同完成 30 幅作品

A

参与义拍，并同时从 13：00 开始制作 (不考虑休息时间，每人做完一幅作品后才能做下一幅)．
①若甲完成的数量比乙完成的 2 倍少 6 幅，求在几时几分恰好全部完成；
②因义拍实际需要，现增加 10 幅作品

B

分配给甲、乙两位同学，并要求尽早完成制作，已知甲、乙每小时分别能做 6 幅和 4 幅作品 B，请你结合方案评价表直接在表格中写出一种作品

A ， B

的分配数量方案．

作品类型	作品 $A$	作品 $B$
分配给甲的数量
分配给乙的数量
方案评价表
方案等级	完成时间	评分
合格	$18 ： 26 \sim 18 ： 36$	1 分
良好	$18 ： 16 \sim 18 ： 26$	2 分
优秀	$18 ： 16$ 前	3 分

查看试题解析

20. 阅读以下微信群聊，完成任务．

任务一：该“旅行团”有几种打车方案？哪种方案比较划算？

任务二：小胡家的两间“亲子家庭房”共花费多少钱？

任务三：该“旅行团”分别购买了“380”和“580”这两种票价的门票各多少张？

查看试题解析

21. 在乐清某校的压花拓展课上，甲、乙两位同学每小时能共做7幅作品A，甲、乙同时开始制作，当甲做了28幅作品A时，乙做了21幅．

(1)、求甲、乙每小时各做多少幅作品A．

(2)、学校组织义拍资助西部贫困学生的活动，甲、乙两位同学计划共同完成30幅作品A参与义拍，并同时从13：00开始制作。（不考虑休息时间，每人做完一幅作品后才能做下一幅）．

①若甲完成的数量比乙完成的2倍少6幅，求在几时几分恰好全部完成．

②因义拍实际需要，现增加10幅作品B分配给甲、乙两位同学，并要求尽早完成制作，已知甲、乙每小时分别能做6幅和4幅作品B，请你结合方案评价表直接在表格中写出一种作品A，B的分配数量方案．

作品类型	作品A	作品B
分配给甲的数量
分配给乙的数
方案评价表
方案等级	完成时间	评分
合格	18：26~18：36	1分
良好	18：16~18：26	2分
优秀	18：16前	3分

查看试题解析

二、数据与统计图表

22. 小林家今年 $1 \sim 5$ 月份的用电量情况如图所示，由图可知，相邻的两个月中，用电量变化最大的是( )

A、1 月至 2 月
B、2 月至 3 月
C、3 月至 4 月
D、4 月至 5 月

查看试题解析
23. 某校为了调查七年级 450 名学生的身高，随机抽取了该年级 100 名学生进行调查，下列说法中，错误的是（）

A、总体是 450 名学生
B、个体是每一名学生的身高
C、样本是 100 名学生的身高
D、样本容量是 100

查看试题解析
24. 从 A 地到 $B$ 地有驾车、公交、地铁三种出行方式，为了选择适合的出行方式，对 6：00~10：00时段这三种出行方式不同时刻出发所用时长 (从 A 地到 B 地) 进行调查、记录与整理，数据如图所示．根据统计图提供的信息，下列推断合理的是( )

A、若 7：00 前出发，则地铁是最快的出行方式
B、若选择公交出行且需要 $30 m i n$ 以内到达，则 7：00 之前出发均可 C、驾车出行所用时长受出发时刻影响较小
D、在此时段里，地铁出行的所用时长都在 $30 m i n$ 至 $40 m i n$ 之间

查看试题解析
25. 某养猪场对 200 头生猪的质量进行统计，得到频数分布直方图 (每一组含前一个边界值，不含后一个边界值) 如图所示，其中质量在 $82.5 k g$ 及以上的生猪有( )

A、20 头
B、50 头
C、140 头
D、200 头

查看试题解析
26. 某工厂上半年生产总值增长率的变化情况如图所示，从图上看，下列结论中不正确的是

A、1~5 月份生产总值增长率逐月减少
B、6 月份生产总值的增长率开始回升
C、这半年中每月的生产总值不断增长
D、这半年中每月的生产总值有增有减

查看试题解析
27. 七(1)班 40 名同学进行 $100 m$ 跑素质测试，测试后体育委员把数据整理后制作频数分布表．把它分成五组，第一组到第三组的频数分别为 $5 ， 7 ， 9$ ，第四组的频率为 0.3 ，则第五组的频数为

查看试题解析
28. 为了解某校初一年级女生的身高情况，随机抽取 60 名学生的身高见下表，则 $m =$ .
分组
$145.5 \sim 150.5$
$150.5 \sim 155.5$
$155.5 \sim 160.5$
$160.5 \sim 165.5$
频数
6
13

$m$
频率

0.55

查看试题解析
29. 期中考试结束后，老师统计了全班 40 人的数学成绩，这 40 个数据共分为 6 组，如果第 $1 \sim 4$ 组的频数分别为 $10 ， 5 ， 7 ， 6$ ，第 5 组的频率为 0.1 ，那么第 6 组的频率是

查看试题解析

30. 某校举行了“我爱古诗词”知识竞赛，全校2000名学生参加，随机抽取部分学生成绩作为样本整理，将他们的成绩（成绩

x

取整数，总分100分）分为

60 \leq x < 70

，

70 \leq x < 80

，

80 \leq x < 90

，

90 \leq x < 100

四组进行统计，并制作了如下统计图表．

“我爱古诗词”知识竞赛成绩频数表

分数	频数	频率
$60 \leq x < 70$	3	0.02
$70 \leq x < 80$		0.18
$80 \leq x < 90$	60	$n$
$90 \leq x < 100$		0.4

请根据以上信息，解答下列问题：

(1)、本次共随机抽取了名学生；

n =

；

(2)、补全频数分布直方图；

(3)、若知识竞赛成绩达到80分及以上才能获奖，请估计全校2000名学生中能获奖的学生共有多少人？

查看试题解析

31. 七(2)班第一组的 12 名同学身高 (单位： $c m$ ) 如下： $162 ， 157 ， 161 ， 164 ， 154 ， 153$ ， $156 ， 168 ， 153 ， 152 ， 165 ， 158$ ，那么身高在 $155 \sim 160 c m$ 的频率是

查看试题解析
32. 某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查，调查的项目有：公共汽车、私家车、电动车、自行车、其他 (每位同学仅选一项)．根据调查结果绘制了如下不完整的频数分布表(见下表)．请根据图表信息解答下列问题：

(1)、本次共抽样调查了多少位学生？

(2)、求频数分布表中 $m$ 和 $n$ 的值．
交通方式
频数
频率
公共汽车
$m$
0.25
私家车
24
0.20
电动车
36
$n$
自行车
18
0.15
其他
12
0.10

查看试题解析
33. 某校为了了解七年级学生跳绳成绩，抽取部分学生进行跳绳成绩检测，根据检测结果制成频数表 (见表 1)．经过一段时间训练后，进行第二次抽测，检测结果见表 2．根据频数表，完成以下问题：
表1 被抽样学生跳绳成绩的频数表
组别/个
频数

$149.5 \sim 159.5$
25

$159.5 \sim 169.5$
28

$169.5 \sim 179.5$
21

$179.5 \sim 189.5$
16

$189.5 \sim 199.5$
10
表2 被抽样学生跳绳成绩的频数表
组别/个
频数

$149.5 \sim 159.5$
32

$159.5 \sim 169.5$
44

$169.5 \sim 179.5$
52

$179.5 \sim 189.5$
42

$189.5 \sim 199.5$
30

(1)、求出第一次、第二次抽样的样本容量．

(2)、现规定学生跳绳 170 个以上 (含 170 个)为达标．小林说： “第二次不达标人数比第一次多，因此这段时间训练效果不理想”；小明说： “第二次达标人数比第一次多，因此这段时间训练效果理想”．请你评价这两位同学的观点，并说明理由．

查看试题解析

34. 为迎接杭州亚运会的召开，某校决定在全校范围内开展亚运知识的宣传教育活动

.

为了了解宣传效果，随机抽取部分学生，并在活动前、后对这些学生进行了两次跟踪测评，两次测评中所有同学的成绩没有低于

30

分，现在将收集的数据制成频数分布直方图

(

每一组包含左端值，不包含右端值

)

和频数表

.

宣传活动后亚运知识成绩频数表：

成绩	$30 - 40$	$40 - 50$	$50 - 60$	$60 ～ 70$	$70 - 80$	$80 - 90$	$90 ～ 100$
频数	$2$	$6$	$6$	$16$	$m$	$30$	$12$

(1)、本次活动共抽取学生；

(2)、宣传活动前，在抽取的学生中成绩人数最多一组的组中值是分；

(3)、表中的

m =

，宣传活动后，在抽取的学生中分数高于

65

分的至少有人，至多有人；

(4)、小聪认为，宣传活动后成绩在

60 ～ 70

的人数为

16

，比活动前减少了

14

人，因此学校开展的宣传活动没有效果

.

请你结合统计图表，说一说小聪的看法是否正确

.

为什么？

查看试题解析

35. 统计某天7：00~9：00段经过高速公路某测速点的汽车的速度(测得的速度为整数，单位km/h)，得到如下频数直方图和扇形统计图.请回答下列问题：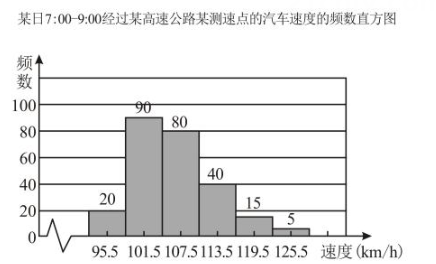

(1)、这一天7：00~9：00经过观察点的车辆总数是多少?

(2)、若该路段汽车限速为110km/h(≤110km/h)，问超速行驶的汽车占总数的百分之几?

查看试题解析

36. 南浔某校研究性学习小组以“学生到学校交通工具类型”为主题对全校学生进行随机抽样调查，调查的项目有：公共汽车、私家车、电动车、自行车、其它（每位同学仅选一项）．根据调查结果绘制了如下不完整的频数分布表和扇形统计图：

交通方式	频数（人数）	频率
公共汽车	m	0.25
私家车	24	0.20
电动车	36	n
自行车	18	0.15
其它	12	0.10

请根据图表信息解答下列问题：

(1)、本次共抽样调查了多少位学生？

(2)、求频数分布表中ｍ和ｎ的值；

(3)、在扇形统计图中，请计算出“电动车”所在的扇形的圆心角的度数．

查看试题解析

分组	$145.5 \sim 150.5$	$150.5 \sim 155.5$	$155.5 \sim 160.5$	$160.5 \sim 165.5$
频数	6	13		$m$
频率			0.55

组别/个	频数
$149.5 \sim 159.5$	25
$159.5 \sim 169.5$	28
$169.5 \sim 179.5$	21
$179.5 \sim 189.5$	16
$189.5 \sim 199.5$	10