命题新趋势3 真实情境（2）——2024年浙教版数学七（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、整式的乘除

1. 芝麻被称为“八谷之冠”，是世界上最古老的油料作物之一，它作为食物和药物，得到广泛的使用.经测算，一粒芝麻的质量约为0.00000209kg，将0.00000209用科学记数法表示为（）

A、 $2.09 \times 1 0_{}^{- 8}$ B、 $0.209 \times 1 0_{}^{- 7}$ C、 $2.09 \times 1 0_{}^{- 6}$ D、 $20.9 \times 1 0_{}^{- 5}$

查看试题解析
2. 世界上最小、最轻的昆虫是膜翅缨小蜂科的一种卵蜂，其质量只有0.000005克，0.000005用科学记数法表示是（）

A、5×10^-6 B、5×10^-5 C、5×10^-4 D、5×10^-3

查看试题解析
3. 小美同学为了验证平方差公式，如图是用边长为 $a$ 的大正方形剪去一个边长为 $b$ 的小正方形后得到的图形 (阴影部分)，通过剪拼，拼成了①②③三种新的图形，其中能够验证平方差公式的是( )

A、①②
B、①③
C、②③
D、①②③

查看试题解析
4. 如图，有两个正方形A ，B ，现将B放在A的内部如图甲，将A ， B并排放置后构造新的正方形如图乙．若图甲和图乙中阴影部分的面积分别为 $\frac{3}{10}$ 和 $\frac{21}{5}$ ，则正方形A与B的面积之和为．
，

查看试题解析
5. 人们以分贝为单位来表示声音的强弱.通常说话的声音是50分贝，它表示声音的强度是10⁵.摩托车发出的声音是110分贝，它表示声音的强度是 10¹¹.飞机发动机的声音是130分贝.飞机发动机的声音强度是说话声音强度的多少倍?

查看试题解析
6. 我们知道纳米（nm）是非常小的长度单位，1 nm=10^-9m，用边长为1 nm的小正方形去铺成一个边长为1 cm的正方形，求需要的小正方形的个数．

查看试题解析
7. 地球可以看作球体，若用V，r分别表示球的体积和半径，则V= $\frac{4}{3}$ πr³ ，已知地球的半径约为6×10³ km，则它的体积大约是多少立方千米(π取3，结果用科学记数法表示)？

查看试题解析
8. 如图，现有一块长为 $(3 a + b)$ 米，宽为 $(a + b)$ 米的长方形地块，规划将阴影部分进行绿化，中间预留部分是边长为 $(2 a - b)$ 米的正方形．

(1)、求绿化的面积S（用含a，b的代数式表示，并化简）；

(2)、若 $a = 3$ ， $b = 2$ ，绿化成本为100元/平方米，则完成绿化共需要多少元？

查看试题解析
9. 小王在学习完全平方公式时，发现 $a - b ， a + b ， a^{2} + b^{2} ， a b$ 这四个代数式之间是有联系的，于是他在研究后提出了以下问题：

(1)、已知 $a + b = 4 ， a^{2} + b^{2} = 10$ ，求 $a b$ 的值．

(2)、已知 $m - \frac{1}{m} = 3$ ，求 $m + \frac{1}{m}$ 的值．

(3)、如图，在长方形 $A B C D$ 中， $A B = 6 c m ， B C = 8 c m$ ，正方形 $A E H G$ 、正方形 $E B K F$ 和正方形 $N K C M$ 都在它的内部，且 $B K > K C$ ．记 $A E = a ， C M = b$ ，若 $a^{2} +$ $b^{2} = 18 {cm}^{2}$ ，求长方形 $P F Q D$ 的面积．
请解决小王提出的这三个问题．

查看试题解析
10. 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片边长为a的正方形，B种纸片是边长为b的正方形，C种纸片长为a、宽为b的长方形，并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．

(1)、请用两种不同的方法求图2中大正方形的面积．
方法1：；方法2：；

(2)、观察图②，请你写出下列三个式子： ${(a + b)}^{2} ， a^{2} + b^{2} ， a b$ 之间的等量关系：；

(3)、根据（2）中的等量关系，解决下列问题；
①已知 $a + b = 5 ， a^{2} + b^{2} = 11$ ，求ab的值；
②已知 ${(x - 2022)}^{2} + {(x - 2024)}^{2} = 34$ ，求 ${(x - 2023)}^{2}$ 的值．

查看试题解析
11. 数学活动课上，老师准备了若干个如图1的三种纸片，A种纸片是边长为a的正方形，B种纸片是边长为b的正方形，C种纸片是长为b，宽为a的长方形．并用A种纸片一张，B种纸片一张，C种纸片两张拼成如图2的大正方形．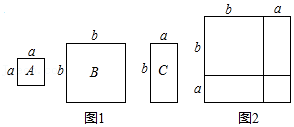

(1)、请用两种不同的方法求图2大正方形的面积：
方法1：；方法2：；

(2)、观察图2，请你写出代数式：（a+b）² ， a²+b² ， ab之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：
①已知：a+b＝5，（a-b）²＝13，求ab的值；

②已知（2023-a）²+（a-2022）²＝5，求（2023-a）（a-2022）的值．

查看试题解析

二、因式分解

12. 将多项式： $16 m^{2} + 1$ 加上一个单项式后，使它能够在我们所学范围内进行因式分解，则此单项式不能是（）

A、-2 B、 $- 15 m^{2}$ C、8m D、-8m

查看试题解析
13. 小南是一位密码编译爱好者，在他的密码手册中有这样一条信息：x- 1，a- b，3，x²+1，a，x+1分别对应下列六个字：思，爱，我，数，学，考，现将 $3 a (x^{2} - 1) - 3 b (x^{2} - 1)$ 分解因式，结果呈现的密码信息可能是（）

A、我爱学 B、我爱数学 C、我爱思考 D、数学思考

查看试题解析
14. 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：a-b，x-y，x+y，a+b，x²-y² ， a²-b² 分别对应下列六个字：江、爱、我、浙、游、美，现将(x²-y²)a²-(x²-y²)b²因式分解，结果呈现的密码信息可能是（）

A、我爱美 B、浙江游 C、爱我浙江 D、美我浙江

查看试题解析
15. 夏老师发现，两位同学将一个二次三项式分解因式时，聪聪同学因看错了一次项而分解成3(x-1)·(x-9)，江江同学因看错了常数项而分解成3(x-2)(x-4)．那么，聪明的你，通过以上信息可以知道，原多项式应该是被因式分解为.

查看试题解析
16. 生活中我们经常用到密码，如手机解锁、密码支付等 $.$ 为方便记忆，有一种用“因式分解”法产生的密码，其原理是：将一个多项式分解成多个因式，如：将多项式 $x^{3} - 9 x$ 分解结果为 $x (x + 3) (x - 3) .$ 当 $x = 20$ 时， $x + 3 = 23$ ， $x - 3 = 17$ ，此时可得到数字密码 $202317 .$ 将多项式 $x^{3} + m x^{2} + n x$ 因式分解后，利用题目中所示的方法，当 $x = 12$ 时可以得到密码 $121415$ ，则 $m n =$ ．

查看试题解析
17. 小刚同学动手剪了如图①所示的正方形与长方形纸片若干张．

(1)、他用1张1号、1张2号和2张3号卡片拼出一个新的图形（如图②）．根据这个图形的面积关系写出一个你所熟悉的乘法公式，这个乘法公式是；

(2)、如果要拼成一个长为（a+2b），宽为（a+b）的大长方形，则需要2号卡片张，3号卡片张；

(3)、当他拼成如图③所示的长方形，根据6张小纸片的面积和等于大纸片（长方形）的面积可以把多项式a²+3ab+2b²分解因式，其结果是；

(4)、动手操作，请你依照小刚的方法，画出拼图并利用拼图分解因式a²+5ab+6b²= ▲ ．

查看试题解析
18. 如图，把一段铁丝分成相等的三段，可围成边长为 $(\frac{1}{3} a^{2} + \frac{13}{3}) (c m)$ 的等边三角形.若把这段铁丝分成相等的四段，则可围成边长为 $(\frac{3}{2} a + 1) (c m)$ 的正方形.求该段铁丝的长.

查看试题解析
19. 小伟同学的作业本上有一道练习题，这道题被除式的第二项和商的第一项不小心被墨水污染了(污染处用字母 M 和N 表示)，污染后的习题如下：
$(30 x^{4} y^{2} + M + 12 x^{2} y^{2}) \div (- 6 x^{2} y) = N + 3 x y - 2 y .$

(1)、请你帮小伟复原被污染的代数式 M和N.

(2)、小伟在进一步练习时将复原后的 N+3xy-2y与代数式 $x^{2} y + x y + y$ 相加，请帮他求出这两个代数式的和，并判断所求的和能否进行因式分解? 若能，请分解因式；若不能，请说明理由.

查看试题解析
20. 下面是某同学对 $(x^{2} - 2 x - 1) (x^{2} - 2 x + 3) + 4$ 进行因式分解的过程，解：设 $x^{2} - 2 x = y$
$原式$ = $(y - 1) (y + 3) + 4 \dots \dots \cdot 第一步$
= $y^{2} + 2 y + 1 \dots \dots 第二步$
= $(y + 1)^{2} \dots \dots 第三步$
= ${(x^{2} - 2 x + 1)}^{2} \dots \dots 第四步$
回答下列问题：

(1)、该同学第二步到第三步运用了
A．提取公因式
B．平方差公式
C．两数和的完全平方公式
D．两数差的完全平方公式

(2)、该同学因式分解的结果是否彻底？(填“彻底”或者“不彻底”)．若不彻底，请直接写出因式分解的最后结果

(3)、请你模仿以上方法尝试对多项式 $(x^{2} - 4 x) (x^{2} - 4 x + 8) + 16$ 进行因式分解．

查看试题解析
21. 小明家的门锁密码采用教材中介绍的“因式分解法”设置，其原理是：将一个多项式分解因式，如多项式x⁴-y⁴可因式分解为(x+y)(x-y)(x²+y²)，当取x=9，y=9时，各个因式的值是：x-y=0，x+y=18，x²+y²=162，于是就把“018162”作为一个六位数密码．类似地，小明采用多项式9x³-4xy²产生密码，当x=11，y=11时，写出能够产生的所有密码．

查看试题解析
22. 小伟同学的错题本上有一题练习题，这道题被除式的第二项和商的第一项不小心被墨水污染了（污染处用字母Ｍ和Ｎ表示），污染后的习题如下：
$(30 x^{4} y^{2} + M + 12 x^{2} y^{2}) \div (- 6 x^{2} y) = N + 3 x y - 2 y .$

(1)、请你帮小伟复原被污染的Ｍ和Ｎ处的代数式，并写出练习题的正确答案；

(2)、爱动脑的小芳同学把练习题的正确答案与代数式ｘ²ｙ＋ｘｙ＋ｙ相加，请帮小芳求出这两个代数式的和，并判断所求的和能否进行因式分解？若能，请分解因式；若不能，请说明理由．

查看试题解析
23. 如图，将一张长方形纸板按图中虚线裁前成九块，其中有两块是边长都为 $m$ 的大正方形，两块是边长都为 $n$ 的小正方形，五块是长为 $m$ ，宽为 $n$ 的同样大小的小长方形，且 $m > n$ .(以上长度单位： $cm$ )

(1)、观察图形，可以发现代数式 $2 m^{2} + 5 m n + 2 n^{2}$ 可以因式分解为.

(2)、若每块小长方形的面积为 $10 {cm}^{2}$ ，四个正方形的面积和为 $58 {cm}^{2}$ .
①试求图中所有裁剪线(虚线部分)长度之和；

②求 ${(m + n)}^{2}$ 的值.

查看试题解析