命题新趋势3 真实情境（1）——2024年浙教版数学七（下）期末复习

试卷更新日期：2024-06-02 类型：复习试卷

进入出卷网下载

一、第一章平行线

1. 请阅读以下“预防近视”知识卡

已知如上图，桌面和水平面平行， $C D$ 与书本所在平面重合，根据卡片内容，请判断正常情况下，坐姿正确且座椅高度适合时，视线 $B C$ 和书本所在平面所成角度 $∠ B C D$ 不可能为以下哪个角度（）

A、 $74 °$ B、 $78 °$ C、 $84 °$ D、 $88 °$

查看试题解析
2. 如图，某公园里有一处长方形风景欣赏区，长 $50$ 米，宽 $25$ 米，为方便游人观赏，特意修建了如图所示的小路（图中非阴影部分），小路的宽均为 $1$ 米，小明沿着小路的中间，从入口 $A$ 到出口 $B$ 所走的路线（图中虚线）长为（）

A、 $96$ 米 B、 $98$ 米 C、 $99$ 米 D、 $100$ 米

查看试题解析
3. 一块长为 $a cm$ ，宽为 $b cm$ 的长方形木板中间有一条裂缝(如图 1 所示)．若把裂缝右边的一块向右平移 $4 c m$ (如图 2 所示)，则这时裂缝的面积是( )

A、 $4 a {cm}^{2}$ B、 $4 b {cm}^{2}$ C、 $(a b - 4 a) {c m}^{2}$ D、 $(a b - 4 b) {c m}^{2}$

查看试题解析
4. 在一次数学活动课上，老师让同学们用两个大小、形状都相同的三角尺画平行线 $A B ， C D$ ，贝贝、晶晶、欢欢三位同学的做法如图所示．上述三位同学的做法中，依据“内错角相等，两直线平行”的是（）

A、仅贝贝同学
B、贝贝和晶晶
C、晶晶和欢欢
D、贝贝和欢欢

查看试题解析
5. 在铺设铁轨时，两条直轨必须是互相平行的，如图，若已经知道 $∠ 2$ 是直角，再度量图中已标出的某个角，仍不能判断两条直轨平行，则该角为（）

A、 $∠ 1$ B、 $∠ 3$ C、 $∠ 4$ D、 $∠ 5$

查看试题解析
6. 如图，在一块长为 $10 m$ ，宽为 $7 m$ 的长方形草地上，有一条路宽为 $1 m$ 的小路，这块草地的绿地面积为 $m^{2}$ ．

查看试题解析
7. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面 $A B$ 与水杯下沿 $C D$ 平行，光线 $E F$ 从空气射向水中时发生折射，光线变成 $F G$ ，点H在光线 $E F$ 所在的直线上，已知 $∠ E F A = 40 °, ∠ F G C = 61 °$ ，求 $∠ G F H$ 的度数．

查看试题解析
8. 综合与实践
问题情境：“综合与实践”课上，老师将一副直角三角板摆放在直线MN上（如图1， $∠ E D C = 9 0^{°}, ∠ D E C = 6 0^{°}, ∠ A B C = 9 0^{°}, ∠ B A C = 4 5^{°}$ ）．保持三角板EDC不动，老师将三角板ABC绕点 $C$ 以每秒 $5^{°}$ 的速度顺时针旋转，旋转时间为 $t$ 秒，当AC与射线CN重合时停止旋转．各小组解决老师给出的问题，又提出新的数学问题，请你解决这些问题.
深入探究：

(1)、老师提出，如图2，当AC转到与∠DCE的角平分线重合时，∠ECB-∠DCA=15°，当AC转到与 $∠ D C E$ 的角平分线重合时， $∠ E C B - ∠ D C A = 1 5^{°}$ ，当AC在 $∠ D C E$ 内部的其他位置时，结论 $∠ E C B - ∠ D C A = 1 5^{°}$ 是否依然成立?请说明理由．

(2)、勤学小组提出：若AC旋转至 $∠ D C E$ 的外部， $∠ D C A$ 与 $∠ E C B$ 是否还存在如上数量关系?若存在，请说明理由；若不存在，请写出 $∠ D C A$ 与 $∠ E C B$ 的数量关系，并说明理由．

(3)、拓展提升：
智慧小组提出：若AC旋转到与射线CM重合时停止旋转．在旋转过程中，直线DE与直线AC是否存在平行的位置关系?若存在，请直接写出 $t$ 的值；若不存在，请说明理由．

查看试题解析
9. 如图是一个“跳棋”棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角，跳动时，每一步只能跳到它的同位角或内错角或同旁内角的位置上.
例如，从起始角∠1跳到终点角∠3，有两种不同的路径：①∠1，∠9，∠3；②∠1，∠12，∠6，∠10，∠3.
问：从起始角∠1 依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点角∠8? 若能，请写出路径；若不能，请说明理由.

查看试题解析
10. 小明完成作业后在家复习，他看到七下课本第12页例4，感到这个结论十分有趣，便尝试探究起来.

(1)、【基础巩固】
与例4条件和结论互换，改成了：“如图1，AP 平分∠BAC，CP平分∠ACD，AB∥CD，则∠1+∠2=90°，”小明认为这个结论正确，你赞同他的想法吗? 请说明理由.

(2)、【尝试探究】
小明发现：若将其中一条角平分线改成AC的垂线，则“∠1+∠2=90°”这个结论不成立.请帮小明完成探究：
如图2，AB∥CD，AP平分∠BAC，CP⊥AC，∠1是AP与AB的夹角，∠2 是CP与CD的夹角.
①若∠2=22°，求∠1的度数.
②试说明：2∠1-∠2=90°.

(3)、【拓展提高】
如图3，若AB∥CD，AP⊥AC，CP平分∠ACD，请直接写出∠1与∠2的数量关系.

查看试题解析
11. 义乌江滨绿廊分布于义乌江两岸，东起阳光大道，南至环城路，全长约14千米，总面积400多万平方米，是市民散步休闲的好去处．为了安全起见计划在某段江两岸安置了两座可旋转探照灯．如图1所示灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是每秒3度，灯B转动的速度是每秒2度，假定江两岸是平行的，即 $P Q ∥ M N$ ，且 $∠ B A M = 2 ∠ Q B A$ ．

(1)、填空： $∠ Q B A =$ $°$ ；

(2)、若灯B射线先转动10秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？

(3)、如图2，若两灯同时开始转动，两灯射出的光束交于点C ，则在灯B射线到达BQ之前，A灯转动秒时， $∠ A C B = 140 °$ ．（在横线处直接写出答案）

查看试题解析
12.

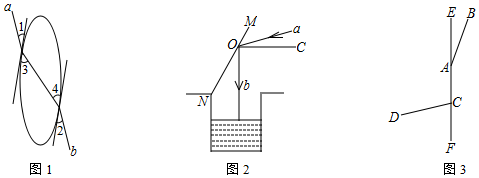(1)、经过薄凸透镜光心的光线，其传播方向不变．如图 $1$ ，光线 $a$ 从空气中射入薄凸透镜，再经过凸透镜的光心，射入到空气中，形成光线 $b$ ，根据光学知识有 $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ，请判断光线 $a$ 与光线 $b$ 是否平行？并说明理由．

(2)、光线照射到镜面会产生反射现象，由光学知识，入射光线与镜面的夹角与反射光线与镜面的夹角相等．如图 $2$ 有一口井，已知入射光线 $a$ 与水平线 $O C$ 的夹角为 $15 °$ ，问如何放置平面镜 $M N$ ，可使反射光线 $b$ 正好垂直照射到井底？ $($ 即求 $M N$ 与水平线 $O C$ 的夹角 $∠ M O C)$

(3)、如图 $3$ ，直线 $E F$ 上有两点 $A$ 、 $C$ ，分别引两条射线 $A B$ 、 $C D . ∠ B A F = 160 °$ ， $∠ D C F = 80 °$ ，射线 $A B$ 、 $C D$ 分别绕 $A$ 点、 $C$ 点以 $2$ 度 $/$ 秒和 $5$ 度 $/$ 秒的速度同时顺时针转动．设时间为 $t$ ，在射线 $C D$ 转动一周的时间内，是否存在某时刻，使得 $C D$ 与 $A B$ 平行？若存在，求出所有满足条件的时间 $t$ ．

查看试题解析

二、第二章二元一次方程组

13. 现用190张铁皮做盒子，每张铁皮做8个盒身或做22个盒底，而一个盒身与两个盒底配成一个盒子，设用x张铁皮做盒身，y张铁皮做盒底，则可列方程组为（　　）

A、 $\{\begin{matrix} x + y = 190 \\ 2 \times 8 x = 22 y \end{matrix}$ B、 $\{\begin{matrix} x + y = 190 \\ 2 \times 22 y = 8 x \end{matrix}$ C、 $\{\begin{matrix} 2 y + x = 190 \\ 8 x = 22 y \end{matrix}$ D、 $\{\begin{matrix} 2 y + x = 190 \\ 2 \times 8 x = 22 y \end{matrix}$

查看试题解析
14. 把一些糖果分给小朋友，如果每人分5粒，分完后还剩4粒，如果每人分6粒，最后一个人只分到1粒，设小朋友的总人数为x人，共有糖果y粒，以下方程组正确的是（　　）

A、 $\{\begin{array}{l} y = 5 x + 4 \\ y = 6 (x - 1) + 1 \end{array}$ B、 $\{\begin{array}{l} 5 x = y - 4 \\ 6 x = y - 1 \end{array}$ C、 $\{\begin{array}{l} 5 x = y + 4 \\ 6 x = y + 5 \end{array}$ D、 $\{\begin{array}{l} y = 5 x + 4 \\ y = 6 x + 1 \end{array}$

查看试题解析
15. 把形状大小完全相同的小长方形卡片（如图1）按不同方式、不同数量、不重叠地放置于相同的大长方形中（如图2、图3），大长方形的一边长为8，其未被卡片覆盖的部分用阴影表示．已知图2和图3阴影部分的周长之比为 $6 ： 7$ ，则大长方形的周长为（　　）

A、29 B、28 C、27 D、26

查看试题解析
16. 我国民间流传着许多趣味算题，它们多以顺口溜的形式表达，其中《孙子算经》中记我了这样一个数学问题：一群老人去赶集，半路买了一堆梨，一人一个多一梨，一人两个少二梨，请问君子知道否，几个老人几个梨？若设有x个老人，y个梨，则可列出的方程组为．

查看试题解析
17. 某眼镜厂有工人25名，每人每天平均生产镜架9个或镜片12片.为了使每天生产的镜架和镜片刚好配套，设x名工人生产镜架，y名工人生产镜片，则可列出方程组：.

查看试题解析
18. 数学课上，老师出示关于x ， y的方程组 ${\begin{array}{l} 3 x - 5 y = 2 a \\ x - 2 y = a - 5 \end{array}$ ，让学生以小组形式展开讨论．展示环节有下列结论：①当 $a = 10$ 时，方程组的解是 ${\begin{array}{l} x = 15 \\ y = 5 \end{array}$ ；②当x ， y的值互为相反数时， $a = 20$ ；③不存在一个实数a使得 $x = y$ ；④若 $x - 3 a = 5$ ，则 $a = 5$ 上述结论中正确的有．

查看试题解析
19. 如图， $A$ 、B两地由公路和铁路相连，在这条路上有一家食品厂，它到 $B$ 地的距离是到 $A$ 地距离的 $2$ 倍，现该食品厂从 $A$ 地购买原料，全部制成食品卖到 $B$ 地（制作过程中有损耗 $）$ ，两次运输 $($ 第一次： $A$ 地 $\to$ 食品厂，第二次：食品厂 $\to B$ 地 $)$ 共支出公路运费 $1$ 5600元，铁路运费 $2$ 0600元．已知公路运费为 $1$ .5元/(千米•吨），铁路运费为 $1$ 元/(千米•吨)．
上图中实线表示公路；虚线表示铁路

(1)、求该食品厂到 $A$ 地， $B$ 地的距离分别是多少千米？

(2)、求该食品厂买进原料及卖出食品各多少吨？

(3)、若该食品厂此次买进的原料每吨花费5000元，要想该批食品销售完后工厂共获利863800元，求卖出的食品每吨售价是多少元？（利润 $=$ 总售价 $-$ 总成本 $-$ 总运费）

查看试题解析

20. 某工厂需制作如图所示的竖式与横式两种无盖纸盒(单位cm).

情境	内容	图形
情境1	工厂仓库内现存有35cm×35cm的正方形纸板200张，35cm×50cm的长方形纸板400张，用库存纸板制作两种无盖纸盒.
情境2	库存纸板已用完，采购部重新采购了如图规格的纸板，甲纸板尺寸为50cm×70cm，乙纸板尺寸为35cm×85cm，丙纸板尺寸为35cm×70cm.采购甲纸板有800张，乙纸板有400张，丙纸板有300张．纸板裁剪后可制作两种无盖纸盒.
情境3	某次采购订单中，甲种纸板的采购数量为500张，乙种300张，因采购单被墨水污染，导致丙种纸板的具体数字已经模糊不清，只知道百位和十位数字分别为2和4.

根据以上信息，解决以下问题：

(1)、情境1，问两种纸盒各做多少个，恰好将库存纸板用完?

(2)、情境2，问能否通过做适当数量的竖式和横式无盖纸盒，使得纸板的使用率为100%?请通过计算说明理由.

(3)、情境3，若本次采购的纸板裁剪做成竖式和横式无盖纸盒，并使得纸板的使用率为100%请你能帮助工厂确定丙纸板的张数.

查看试题解析

21. 根据以下素材，探索完成任务．

如何设计板材裁切方案？
素材1	图1中是一张学生椅，主要由靠背、座垫及铁架组成.测量，该款学生椅的靠背尺寸为 $40 c m \times 15 c m$ ，座垫尺寸为 $40 c m \times 35 c m$ .图2是靠背与座垫的尺寸示意图．
素材2	因学校需要，某工厂配合制作该款式学生椅.经清点库存时发现，工厂仓库已有大量的学生椅铁架，只需在市场上购进某型号板材加工制做该款式学生椅的靠背与座垫.已知该板材长为 $240 c m$ ，宽为 $40 c m$ .（裁切时不计损耗）
我是板材裁切师
任务一	拟定裁切方案	若要不造成板材浪费，请你设计出一张该板材的所有裁切方法．方法一：裁切靠背16张和座垫0张．方法二：裁切靠背张和坐垫张. 方法三：裁切靠背张和坐垫张.
任务二	确定搭配数量	若该工厂购进50张该型号板材，能制作成多少张学生椅？
任务三	解决实际问题	现需要制作700张学生椅，该工厂仓库现有1张座垫和11张靠背，还需要购买该型号板材多少张（恰好全部用完）？并给出一种裁切方案．

查看试题解析

22. 声音在空气中传播的速度随温度的变化而变化，科学家已测得一定温度下声音传播的速度如下表．如果用v表示声音在空气中的传播速度，t 表示温度，则v， t满足公式： v=at+b (a， b为已知数)．

气温(℃) 声音传播的速度(米/秒)

-20 318

-10 324

0 330

10 336

20 342

30 348

(1)、求a，b的值

(2)、若温度是100℃时，问声音在空气中的传播速度是多少？

查看试题解析

气温(℃)	声音传播的速度(米/秒)
-20	318
-10	324
0	330
10	336
20	342
30	348

命题新趋势3 真实情境（1）——2024年浙教版数学七（下）期末复习

一、第一章 平行线

二、第二章 二元一次方程组

一、第一章平行线

二、第二章二元一次方程组