命题新趋势2 学科融合——2024年北师大版数学七(下)期末复习
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 物理中有一种现象,叫折射现象,它指的是当光线从空气射入水中时,光线的传播方向会发生改变.如图,我们建立折射现象数学模型,表示水面,它与底面平行,光线从空气射入水里时发生了折射,变成光线射到水底处,射线是光线的延长线.若 , 则的度数为( )
 A、 B、 C、 D、2. 据中新网报道,中国科学技术大学完成的“祖冲之二号”和“九章二号”量子计算优越性实验入选2021年国际物理学十大进展,人们发现全球目前最快的超级计算机用时2.3秒的计算量,“祖冲之二号”大约用时仅为0.00000022秒,将数字0.00000022用科学记数法表示为( )A、 B、 C、 D、3. 弹簧挂上物体后伸长,已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:下列说法错误的是( )
A、 B、 C、 D、2. 据中新网报道,中国科学技术大学完成的“祖冲之二号”和“九章二号”量子计算优越性实验入选2021年国际物理学十大进展,人们发现全球目前最快的超级计算机用时2.3秒的计算量,“祖冲之二号”大约用时仅为0.00000022秒,将数字0.00000022用科学记数法表示为( )A、 B、 C、 D、3. 弹簧挂上物体后伸长,已知一弹簧的长度()与所挂物体的质量()之间的关系如下表:下列说法错误的是( )物体的质量()
0
1
2
3
4
5
弹簧的长度()
10
15
20
A、在没挂物体时,弹簧的长度为 B、弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量 C、在弹簧能承受的范围内,所挂物体的质量每增加 , 弹簧的长度就增加 D、在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为4. 氧气是由氧元素形成的一种单质,氧元素的原子半径约为 , 则氧原子的半径用科学记数法表示为( )A、 B、 C、 D、5. 水是生物赖以生存的必要物质,经测算,一个水分子的直径约有0.0000004mm , 数据“0.0000004”用科学记数法表示为( )A、4×10﹣6 B、4×10﹣7 C、0.4×10﹣6 D、4×1076. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为0.000 688毫米,则0.000 688可用科学记数法表示为( )A、 B、 C、 D、7. 如图,下面是物理课上测量铁块A的体积实验,将铁块匀速向上提起,直至完全露出水面一定高度,下面能反映这一过程中,液面高度h与铁块被提起的时间t之间的大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 反物质理论是当代物理研究中的重大突破,科学家们一直在致力于寻找反物质存在的证据,现捕捉到某种微粒子,测得它的质量为0.0000000674克,这个质量用科学记数法表示为( )A、克 B、克 C、克 D、克9. 根据实验结果表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的重量间有下表的关系,下列说法不正确的是( )
8. 反物质理论是当代物理研究中的重大突破,科学家们一直在致力于寻找反物质存在的证据,现捕捉到某种微粒子,测得它的质量为0.0000000674克,这个质量用科学记数法表示为( )A、克 B、克 C、克 D、克9. 根据实验结果表明,在弹簧的承受范围内,弹簧挂上物体后会伸长,测得一弹簧的长度与所挂的物体的重量间有下表的关系,下列说法不正确的是( )0
1
2
3
4
20
21
22
23
24
A、x与y都是变量,且x是自变量,y是因变量 B、在弹性范围内,随着所挂物体重量的增加,弹簧长度逐渐变长 C、弹簧不挂重物时的长度为 D、在弹性范围内,所挂物体的重量每增加 , 弹簧长度增加10. 弹簧挂上物体后伸长,已知一弹簧的长度与所挂物体的质量之间的关系如表:下列说法错误的是( )物体的质量
弹簧的长度
A、在没挂物体时,弹簧的长度为 B、弹簧的长度随物体的质量的变化而变化,物体的质量是因变量,弹簧的长度是自变量 C、在弹簧能承受的范围内,所挂物体的质量每增加 , 弹簧的长度就增加 D、在弹簧能承受的范围内,当物体的质量为时,弹簧的长度为11. 如图,在实验课上,小亮利用同一块木板,测量了小车从木板顶部下滑的时间与支撑物的高度 , 得到如下表所示的数据.下列结论不正确的是( )木板的支撑物高度
…
下滑时间
…
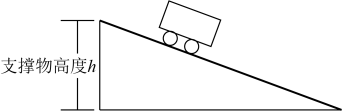 A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短12. 在实验课上,小亮利用同一块木板测得小车从不同高度下滑的时间,支撑物高度()与下滑的时间()的关系如下表:
A、这个实验中,木板的支撑物高度是自变量 B、支撑物高度每增加 , 下滑时间就会减少 C、当时,为 D、随着支撑物高度的增加,下滑时间越来越短12. 在实验课上,小亮利用同一块木板测得小车从不同高度下滑的时间,支撑物高度()与下滑的时间()的关系如下表:支撑物高()
10
20
30
40
50
下滑时间()
3.25
3.01
2.81
2.66
2.56
以下结论错误的是( )
A、当时,为 B、随支撑物高度增加,下滑时间越来越短 C、支撑物高度每增加 , 下滑时间就会减少 D、估计当时,小于13. 世界上最早记载潜望镜原理的古书,是公元前二世纪中国的《淮南万毕术》.书中记载了这样的一段话:“取大镜高悬,置水盘于其下,则见四邻矣”.现代潜艇潜望镜是在20世纪初发明的.如图是潜望镜工作原理的示意图,那么它所应用的数学原理是( ) A、内错角相等,两直线平行 B、同旁内角互补,两直线平行 C、对顶角相等 D、两点确定一条直线14. 生物具有遗传多样性,遗传信息大多储存在分子上.一个分子的直径约为.这个数量用科学记数法表示为( )A、 B、 C、 D、15. 某生物实验小组研究发现,某种种子发芽率与浸泡时间有下面关系,下列说法正确的是( )
A、内错角相等,两直线平行 B、同旁内角互补,两直线平行 C、对顶角相等 D、两点确定一条直线14. 生物具有遗传多样性,遗传信息大多储存在分子上.一个分子的直径约为.这个数量用科学记数法表示为( )A、 B、 C、 D、15. 某生物实验小组研究发现,某种种子发芽率与浸泡时间有下面关系,下列说法正确的是( )浸泡时间/时
0
2
6
8
10
12
14
16
20
发芽率/%
15.9
26.1
32.3
35
53
61
43.1
10.8
30.5
A、种子发芽率为自变量,种子浸泡时间为因变量 B、随着种子浸泡时间的加大,种子发芽率在提高 C、随着种子浸泡时间的加大,种子发芽率在降低 D、由表格可以看出,种子浸泡时间为12小时左右比较适宜16. 公元前200年,古希腊地理学家埃拉托色尼将天文学与测地学结合起来测量地球圆周,他提出设想:在夏至日那天,分别在两地同时观察太阳的位置,并根据地物阴影的长度差异,加以研究分析,从而总结出计算地球圆周的科学方法.他发现,在当时的城市塞恩(图中的A点),直立的杆子在某个时刻没有影子,而此时在500英里以外的亚历山大(图中的B点),直立的杆子的影子却偏离垂直方向(图中角等于).根据这个数据,可以算出地球一周的总长约等于 , 这是因为弧AB的长地球周长的缘故,其中弧AB的长大约为 . 题目中运用到的平行线相关定理是( ) A、对顶角相等 B、两直线平行,同位角相等 C、同旁内角互补,两直线平行 D、两直线平行,内错角相等17. 太阳能作为一种新型能源,被广泛应用到实际生活中,在利用太阳能热水器来加热的过程中,热水器里水的温度随着太阳光照射时间的变化而变化,这一变化过程中因变量是( )A、热水器里水的温度 B、太阳光的强弱 C、太阳光照射的时间 D、热水器的容积18. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )
A、对顶角相等 B、两直线平行,同位角相等 C、同旁内角互补,两直线平行 D、两直线平行,内错角相等17. 太阳能作为一种新型能源,被广泛应用到实际生活中,在利用太阳能热水器来加热的过程中,热水器里水的温度随着太阳光照射时间的变化而变化,这一变化过程中因变量是( )A、热水器里水的温度 B、太阳光的强弱 C、太阳光照射的时间 D、热水器的容积18. 如图1,当光从空气进入水中时,会发生折射,满足入射角∠1 与折射角∠2 的度数比为4:3.如图2,在同一平面上,两条光线同时从空气进入水中,两条入射光线与水面的夹角分别为α,β,水中两条折射光线的夹角为γ,则α,β,γ三者之间的数量关系为( )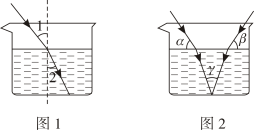 A、 B、 C、α+β=γ D、
A、 B、 C、α+β=γ D、二、填空题
-
19. 光的速度每秒约米,地球和太阳的距离约是米,则太阳光从太阳射到地球需要秒.20. 碳纳米管的硬度与金刚石相当,却拥有良好的柔软性,我国某物理研究组已研制出直径为0.00000000052米的碳纳米管,将0.00000000052用科学记数法表示为 .21. 某微生物的直径为0.00004035m,这个数用科学记数法表示为 .22. 某种樱桃营养丰富,富含铁、维生素A、B、C及钙、磷等矿质元素.每克该种樱桃含维生素C不低于克.将用科学记数法表示为 .23. 埃是表示极小长度的单位名称,是为纪念瑞典物理学家埃斯特朗而命名的.1埃等于一亿分之一厘米,用科学记数法表示:1埃等于cm.24. 物理中有一种现象,叫折射现象,它指的是当光线从空气射入水中时,光线的传播方向会发生改变.如图,我们建立折射现象数学模型,表示水面,它与底面平行,光线从空气射入水里时发生了折射,变成光线射到水底处,射线是光线的延长线, , , 则的度数为°.
 25. 从汽车灯的点 处发出的一束光线经灯的反光罩反射后沿 方向平行射出, 已知入射光线 的反射光线为 . 在如图所示的截面内, 若入射光线 经反光罩反射后沿 射出, 且 , 则
25. 从汽车灯的点 处发出的一束光线经灯的反光罩反射后沿 方向平行射出, 已知入射光线 的反射光线为 . 在如图所示的截面内, 若入射光线 经反光罩反射后沿 射出, 且 , 则 26. 如图是地球截面图,其中 , 分别表示赤道和南回归线,冬至正午时,太阳光直射南回归线(太阳光线的延长线经过地心),此时,太阳光线与地面水平线垂直,已知 , 则的度数是 .
26. 如图是地球截面图,其中 , 分别表示赤道和南回归线,冬至正午时,太阳光直射南回归线(太阳光线的延长线经过地心),此时,太阳光线与地面水平线垂直,已知 , 则的度数是 . 27. 如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE , DF的反向延长线交于主光轴MN上一点P . 若∠ABE=150°,∠CDF=160°,则∠EPF的度数是 .
27. 如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE , DF的反向延长线交于主光轴MN上一点P . 若∠ABE=150°,∠CDF=160°,则∠EPF的度数是 . 28. 埃拉托斯特尼是古希腊著名的地理学家,他曾巧妙估算出地球的周长.如图,处是塞尼城中的一口深井,夏至日中午12时,太阳光可直射井底.处为亚历山大城,它与塞尼城几乎司一条经线上,两地距离约为800km,于是地球周长可近似为 , 太阳光线看作平行光线,他在亚历山大城测得天顶方向与太阳光线的夹角为7.2°.根据可以推导出的大小,依据是;埃拉托斯特尼估算得到的地球周长约为km.
28. 埃拉托斯特尼是古希腊著名的地理学家,他曾巧妙估算出地球的周长.如图,处是塞尼城中的一口深井,夏至日中午12时,太阳光可直射井底.处为亚历山大城,它与塞尼城几乎司一条经线上,两地距离约为800km,于是地球周长可近似为 , 太阳光线看作平行光线,他在亚历山大城测得天顶方向与太阳光线的夹角为7.2°.根据可以推导出的大小,依据是;埃拉托斯特尼估算得到的地球周长约为km. 29. 为了响应国家的节能号召,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线的最大夹角为 62°如图,电板 AB与最大夹角时刻的太阳光线互相垂直,而与此同时电池板 CD 与水平线的夹角为 48°要使 CD/AB,需将电池板 CD绕支点逆时针旋转角a,则°(0<a<90).
29. 为了响应国家的节能号召,某市公交站亭装上了太阳能电池板.当地某一季节的太阳光(平行光线)与水平线的最大夹角为 62°如图,电板 AB与最大夹角时刻的太阳光线互相垂直,而与此同时电池板 CD 与水平线的夹角为 48°要使 CD/AB,需将电池板 CD绕支点逆时针旋转角a,则°(0<a<90).
三、解答题
-
30. 如果甲球的半径是乙球的 n倍,那么甲球的体积是乙球的 n3倍.地球、木星、太阳都可以近似地看做是球体,木星、太阳的半径分别约是地球的 10 倍和102 倍,它们的体积分别约是地球的多少倍?
四、综合题
-
31. 小红的物理老师说:“离地面越高,气温越低,高地面的高度每上升1千米,气温会下降6℃”,小红测得此时地面的气温为20℃.(1)、物理老师描述了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、根据物理老师的描述,请把温度的变化情况填入下表:
离地面高度(千米)
0
1
2
3
4
温度(摄氏度)
(3)、在方格纸中,把离地面0千米、1千米、2千米、3千米、4千米高度的温度表示出来. (4)、请你预测离地面高度为5千米时,气温为多少摄氏度?32. 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,恰有两束平行光线从水中射向空气,∠1=30°,∠2=130°.
(4)、请你预测离地面高度为5千米时,气温为多少摄氏度?32. 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,恰有两束平行光线从水中射向空气,∠1=30°,∠2=130°. (1)、分别指出图中的两对同位角,一对内错角;(2)、求∠3,∠5,∠8的度数,并判断∠1和∠4是否互补.33. 一个长方形台球桌面如图1所示,已知台球在与台球桌边缘碰撞的过程中,撞击线路与桌边的夹角等于反弹线路与桌边的夹角,即图1中的.
(1)、分别指出图中的两对同位角,一对内错角;(2)、求∠3,∠5,∠8的度数,并判断∠1和∠4是否互补.33. 一个长方形台球桌面如图1所示,已知台球在与台球桌边缘碰撞的过程中,撞击线路与桌边的夹角等于反弹线路与桌边的夹角,即图1中的. (1)、台球经过如图2所示的两次碰撞后,第二次的反弹线路为.若开始时的撞击线路为 , 求证:;(2)、台球桌因为长期使用,导致桌角松动变形如图3,在台球经过两次撞击之后,开始时的撞击线路EF所在直线与第二次的反弹线路所在直线相交于点M,若 , 求的度数.34. 下表是某校生物兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
(1)、台球经过如图2所示的两次碰撞后,第二次的反弹线路为.若开始时的撞击线路为 , 求证:;(2)、台球桌因为长期使用,导致桌角松动变形如图3,在台球经过两次撞击之后,开始时的撞击线路EF所在直线与第二次的反弹线路所在直线相交于点M,若 , 求的度数.34. 下表是某校生物兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:试验的种子数
100
200
500
1000
2000
5000
发芽的粒数
94
475
954
1906
4748
发芽频率
0.94
0.955
0.946
0.953
0.9496
(1)、上表中的a= , b=.(2)、任取一粒这种植物种子,它能发芽的概率的估计值是(精确到0.01);(3)、若该校劳动基地需要这种植物幼苗9500棵,试估算需要准备多少粒种子进行发芽培育.35. 光线反射是一种常见的物理现象,在生活中有广泛地应用.例如提词器可以帮助演讲者在看演讲词的同时也能面对摄像机,自行车尾部的反光镜等就是应用了光的反射原理.
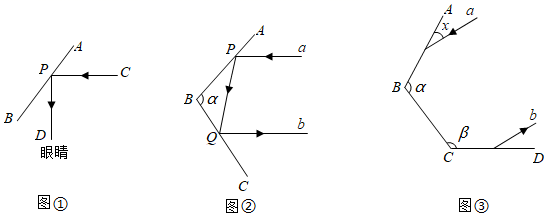 (1)、提词器的原理如图①,AB表示平面镜,CP表示入射光线,PD表示反射光线,∠CPD=90°,求∠APC的度数;(2)、自行车尾部的反光镜在车灯照射下,能把光线按原来的方向返回(如图②),a表示入射光线,b表示反射光线,a∥b.平面镜AB与BC的夹角∠ABC= ,求 .(3)、如图③,若 =108°,设平面镜CD与BC的夹角∠BCD= (90°< <180°),入射光线a与平面镜AB的夹角为x(0°<x<90°),已知入射光线a从平面镜AB开始反射,经过2或3次反射,当反射光线b与入射光线a平行时,请直接写出 的度数.(可用含x的代数式表示).
(1)、提词器的原理如图①,AB表示平面镜,CP表示入射光线,PD表示反射光线,∠CPD=90°,求∠APC的度数;(2)、自行车尾部的反光镜在车灯照射下,能把光线按原来的方向返回(如图②),a表示入射光线,b表示反射光线,a∥b.平面镜AB与BC的夹角∠ABC= ,求 .(3)、如图③,若 =108°,设平面镜CD与BC的夹角∠BCD= (90°< <180°),入射光线a与平面镜AB的夹角为x(0°<x<90°),已知入射光线a从平面镜AB开始反射,经过2或3次反射,当反射光线b与入射光线a平行时,请直接写出 的度数.(可用含x的代数式表示).五、实践探究题
-
36. 请解答下列各题:
(1)阅读并回答:科学实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的角相等.如图1,一束平行光线与射向一个水平镜面后被反射,此时 , .
①由条件可知: , 依据是 , , 依据是 .
②反射光线与平行,依据是 .
(2)解决问题:如图2,一束光线射到平面镜上,被反射到平面镜上,又被镜反射,若射出的光线平行于 , 且 , 则 ; .
 37. 在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
37. 在物理学中,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线射到平面镜上,被反射后的光线为 , 则入射光线、反射光线与平面镜所夹的锐角 .
 (1)、【简单应用】
(1)、【简单应用】如图2,有一口井,已知入射光线与水平线的夹角为 , 现放置平面镜 , 可使反射光线正好垂直照射到井底(即射线),与水平线的夹角的度数为 .
(2)、【类比拓展】如图3,有两块平面镜 , 且 , 入射光线经过两次反射,得到反射光线 . 由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即: . 在这样的条件下,求证: .
(3)、【尝试探究】两块平面镜 , 且 , 入射光线经过两次反射,得到反射光线 . 如图4,光线与相交于点 , 则的度数是多少?(用含的式子表示)(三角形内角和)
38. 【问题背景】光线照射到镜面会产生反射现象,小圳在做镜面反射实验时发现:当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.例如:在图1中,有 .
 (1)、【初步探究】如图2,设镜子AB与BC的夹角 , 当时,小圳发现入射光线EF与反射光线GH恰好平行.(2)、【深入探究】如图3,小圳渐渐改变两镜面之间夹角,使得是一个锐角,从F点发出一条光线EF经过2次反射又回到了点F , 入射光线EF与第2次反射光线GF的夹角为 . 用含的式子表示 .(3)、【拓展应用】如图4,小圳继续改变两镜面之间夹角,使得 , 若也是一个钝角,入射光线EF与镜面AB的夹角 . 已知入射光线EF从镜面AB开始反射,经过3次反射,当第3次反射光线与入射光线EF平行时,求出的度数.39. 如图1,自行车尾灯是由塑料罩片包裹的若干个小平面镜组成,利用平面镜反射光线,以提醒后方车辆注意.小亮所在学习小组对其工作原理进行探究,发现以下规律:如图2,EF为平面镜,AB , BC分别为入射光线和反射光线,则∠ABE=∠CBF . 请继续以下探究:
(1)、【初步探究】如图2,设镜子AB与BC的夹角 , 当时,小圳发现入射光线EF与反射光线GH恰好平行.(2)、【深入探究】如图3,小圳渐渐改变两镜面之间夹角,使得是一个锐角,从F点发出一条光线EF经过2次反射又回到了点F , 入射光线EF与第2次反射光线GF的夹角为 . 用含的式子表示 .(3)、【拓展应用】如图4,小圳继续改变两镜面之间夹角,使得 , 若也是一个钝角,入射光线EF与镜面AB的夹角 . 已知入射光线EF从镜面AB开始反射,经过3次反射,当第3次反射光线与入射光线EF平行时,求出的度数.39. 如图1,自行车尾灯是由塑料罩片包裹的若干个小平面镜组成,利用平面镜反射光线,以提醒后方车辆注意.小亮所在学习小组对其工作原理进行探究,发现以下规律:如图2,EF为平面镜,AB , BC分别为入射光线和反射光线,则∠ABE=∠CBF . 请继续以下探究: (1)、探究反射规律
(1)、探究反射规律①如图3,∠ABE=α,∠BFC=105°,则∠DCG= ▲(用含α的代数式表示).
②若光线AB∥CD , 判断EF与FG的位置关系,并说明理由.
(2)、模拟应用研究在行驶过程中,后车驾驶员平视前方,且视点D会高于反射点C(如图4),因此小亮认为反射光线CD应与水平视线DH成一定角度.学习小组设计了如图5所示的模拟实验装置,使入射光线AB∥DH , 当CD与DH所成夹角为15°时,求∠BFC的度数.
40. 【学科融合】物理学中把经过入射点O并垂直于反射面的直线ON叫做法线,入射光线与法线的夹角i叫做入射角,反射光线与法线的夹角r叫做反射角(如图①).由此可以归纳出如下的规律:
在反射现象中,反射光线、入射光线和法线都在同一平面内;反射光线、入射光线分别位于法线两侧;反射角等于入射角.这就是光的反射定律(rfectionlaw).
【数学推理】如图1,有两块平面镜OM,ON,且OM⊥ON,入射光线AB经过两次反射,得到反射光线CD.由以上光的反射定律,可知入射角与反射角相等,进而可以推得他们的余角也相等,即:∠1=∠2,∠3=∠4.在这样的条件下,求证:AB∥CD.
【尝试探究】两块平面镜OM,ON,且∠MON=α,入射光线AB经过两次反射,得到反射光线CD.
 (1)、如图2,光线AB与CD相交于点E,则∠BEC=;(2)、如图3,光线AB与CD所在的直线相交于点E,CBED=β,则α与β之间满足的等量关系是.41. 阅读下列材料,并完成任务.
(1)、如图2,光线AB与CD相交于点E,则∠BEC=;(2)、如图3,光线AB与CD所在的直线相交于点E,CBED=β,则α与β之间满足的等量关系是.41. 阅读下列材料,并完成任务.光线在不同介质中的传播速度是不同的,因此当光线从水中斜射向空气中时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中的折射光线也是平行的.如图,水面与杯底平行,光线与平行,与平行.兴趣小组发现 . 证明过程如下:

证明:∵ ,
∴(依据),
∵ ,
∴ ,
∴ ,
∴ .
(1)、任务一:上述材料中的“依据”指的是:;(2)、任务二:若 , 求的度数.42. 【学科融合】物理学中把经过入射点并垂直于反射面的直线叫做法线,入射光线与法线的夹角叫入射角,反射光线与法线的夹角叫反射角(如图),可得规律:在反射现象中,反射光线、入射光线和法线都在同一个平面内;反射光线和入射光线分别位于法线两侧;入射角等于反射角.这就是光的反射定律.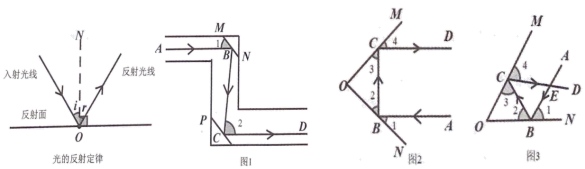 (1)、【问题解决】如图1,潜望镜中的两面镜子是互相平行放置的,已知入射光线与平面镜的夹角 , 那么入射光线经过两次反射以后,两反射光线形成的夹角;(2)、如图2,当两个平面镜 , 夹角是多少度时?可以使任何射到平面镜上的入射光线 , 经过平面镜 , 两次反射后,得到 , 请说明理由;(3)、【尝试探究】两块平面镜 , , 且 , 入射光线经过两次反射,得到反射光线 , 如图3,光线与相交于点 , 求的度数(结果用含的式子表示).
(1)、【问题解决】如图1,潜望镜中的两面镜子是互相平行放置的,已知入射光线与平面镜的夹角 , 那么入射光线经过两次反射以后,两反射光线形成的夹角;(2)、如图2,当两个平面镜 , 夹角是多少度时?可以使任何射到平面镜上的入射光线 , 经过平面镜 , 两次反射后,得到 , 请说明理由;(3)、【尝试探究】两块平面镜 , , 且 , 入射光线经过两次反射,得到反射光线 , 如图3,光线与相交于点 , 求的度数(结果用含的式子表示).
-