命题新趋势1 数学文化——2024年北师大版数学八(下)期末复习
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 围棋起源于中国,古代称之为“弈”,至今已有多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )A、
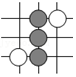 B、
B、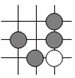 C、
C、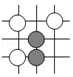 D、
D、 2. 瓷器上的纹饰是中国古代传统文化的重要载体之一,下面花纹图案中既是轴对称图形又是中心对称图形的是( )A、
2. 瓷器上的纹饰是中国古代传统文化的重要载体之一,下面花纹图案中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 瓦当,是指古代中国建筑中覆盖建筑檐头筒瓦前端的遮挡.瓦当上刻有文字、图案,也有用四方之神“朱雀”“玄武”“青龙”“白虎”做图案的.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )
3. 瓦当,是指古代中国建筑中覆盖建筑檐头筒瓦前端的遮挡.瓦当上刻有文字、图案,也有用四方之神“朱雀”“玄武”“青龙”“白虎”做图案的.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着竖冰出现裂纹并开始消融,形状无一定规律,代表一种自然和谐美.图②是从图①的冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=( )
4. 如图,①是我国古代建筑中的一种窗格,其中冰裂纹图案象征着竖冰出现裂纹并开始消融,形状无一定规律,代表一种自然和谐美.图②是从图①的冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=( ) A、72° B、108° C、360° D、540°5. 中国古代的铜锁制作都十分精美,下面的四把锁中,从形状上看是中心对称图形的是( )A、
A、72° B、108° C、360° D、540°5. 中国古代的铜锁制作都十分精美,下面的四把锁中,从形状上看是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. “二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图,其中文字上面图案是中心对称图形的是( )A、
6. “二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图,其中文字上面图案是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 7. 云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中.下列云纹图案中,是中心对称图形的是( )A、
7. 云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中.下列云纹图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 下列图案是我国传统文化中的“福禄寿喜”图,其中中心对称图形是( )A、
8. 下列图案是我国传统文化中的“福禄寿喜”图,其中中心对称图形是( )A、 B、
B、 C、
C、 D、
D、 9. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕、年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中,是轴对称图形,但不是中心对称图形的是( )A、
9. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕、年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 下面四个图形体现了中华民族的传统文化,其中是中心对称图形的是( )A、
10. 下面四个图形体现了中华民族的传统文化,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 11. 《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )A、
11. 《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 12. 国家级非物质文化遗产松桃苗绣,构图夸张浪漫,颜色素净淡雅,以花鸟虫鱼,飞禽走兽等为题材,体现苗族人民向往自由与和平的精神世界.以下四副苗绣图样中,是中心对称图形的是( )A、
12. 国家级非物质文化遗产松桃苗绣,构图夸张浪漫,颜色素净淡雅,以花鸟虫鱼,飞禽走兽等为题材,体现苗族人民向往自由与和平的精神世界.以下四副苗绣图样中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 13. 图书馆的标志是浓缩图书馆文化的符号,下列图书馆标志中,是中心对称图形的是( )A、
13. 图书馆的标志是浓缩图书馆文化的符号,下列图书馆标志中,是中心对称图形的是( )A、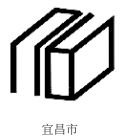 B、
B、 C、
C、 D、
D、 14. 民族图案是数学文化中的瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是( )A、
14. 民族图案是数学文化中的瑰宝.下列图案中,是轴对称图形但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 15. 地铁是城市生活中的重要交通工具,地铁标志作为城市地铁的形象和符号,出现在城市的每个角落,它是城市文化的缩影.下列城市地铁的标志图案中,既是轴对称图形又是中心对称图形的是( )A、
15. 地铁是城市生活中的重要交通工具,地铁标志作为城市地铁的形象和符号,出现在城市的每个角落,它是城市文化的缩影.下列城市地铁的标志图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 16. 窗棂即窗格(窗里面的横的、竖的或斜的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种化纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中,既是轴对称图形又是中心对称图形的是( )A、
16. 窗棂即窗格(窗里面的横的、竖的或斜的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种化纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 17. 简简单单的七巧板能拼出千变万化的图形.殊不知七巧板作为中国传统玩具在国外也甚为流传,被称为“唐图”.下面四幅七巧板拼图的形状是中心对称图形的是( )A、
17. 简简单单的七巧板能拼出千变万化的图形.殊不知七巧板作为中国传统玩具在国外也甚为流传,被称为“唐图”.下面四幅七巧板拼图的形状是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 18. 在我国古代的房屋建筑中,窗棂是重要的组成部分,具有高度的艺术价值.下列窗棂的图案中,是中心对称图形但不是轴对称图形的是( )A、
18. 在我国古代的房屋建筑中,窗棂是重要的组成部分,具有高度的艺术价值.下列窗棂的图案中,是中心对称图形但不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 19. 《九章算术》是中国古代数学名著,其中记载:每头牛比每只羊贵1两,20两买牛,15两买羊,买得牛羊的数量相等,则每头牛的价格为多少两?若设每头牛的价格为x两,则可列方程为( )A、 B、 C、 D、20. 九章算术中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天,已知快马的速度是慢马的倍,求规定时间,设规定时间为天,则可列出正确的方程为( )A、 B、 C、 D、21. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为13,则小正方形的面积为( )
19. 《九章算术》是中国古代数学名著,其中记载:每头牛比每只羊贵1两,20两买牛,15两买羊,买得牛羊的数量相等,则每头牛的价格为多少两?若设每头牛的价格为x两,则可列方程为( )A、 B、 C、 D、20. 九章算术中有一道关于古代驿站送信的题目,其白话译文为:一份文件,若用慢马送到里远的城市,所需时间比规定时间多天;若改为快马派送,则所需时间比规定时间少天,已知快马的速度是慢马的倍,求规定时间,设规定时间为天,则可列出正确的方程为( )A、 B、 C、 D、21. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为13,则小正方形的面积为( )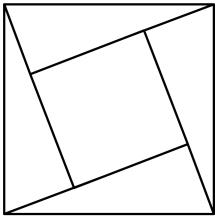 A、3 B、4 C、5 D、622. 《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽,每株脚钱三文足,无钱准与一株椽.”大意是:现请人代买一批椽,这批橡的价钱为6210文,如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?(椽,装于屋顶以支持屋顶材料的木杆)设这批椽有株,则符合题意的方程是( )A、 B、 C、 D、23. 赛龙舟是端午节的主要习俗之一,也是中国民俗传统与运动精神的完美结合.2019年起,深圳大沙河生态长廊龙舟邀请赛连续4年举办,已然成为深圳市标志性的体育赛事.2022年龙舟邀请赛设置了标准龙舟(22人龙舟)500米直道竞速赛项目,其中甲、乙两队参加比赛(比赛起点相同),甲队每秒的速度比乙队快0.5米,结果甲队比乙队提前14秒到达终点.设甲队的速度为米/秒,下列方程正确的是( )A、 B、 C、 D、
A、3 B、4 C、5 D、622. 《四元玉鉴》是我国古代数学重要著作之一,为元代数学家朱世杰所著,该著作记载了“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽,每株脚钱三文足,无钱准与一株椽.”大意是:现请人代买一批椽,这批橡的价钱为6210文,如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?(椽,装于屋顶以支持屋顶材料的木杆)设这批椽有株,则符合题意的方程是( )A、 B、 C、 D、23. 赛龙舟是端午节的主要习俗之一,也是中国民俗传统与运动精神的完美结合.2019年起,深圳大沙河生态长廊龙舟邀请赛连续4年举办,已然成为深圳市标志性的体育赛事.2022年龙舟邀请赛设置了标准龙舟(22人龙舟)500米直道竞速赛项目,其中甲、乙两队参加比赛(比赛起点相同),甲队每秒的速度比乙队快0.5米,结果甲队比乙队提前14秒到达终点.设甲队的速度为米/秒,下列方程正确的是( )A、 B、 C、 D、二、填空题
-
24. 图①是我国古代建筑中的一种窗格.其中冰裂纹图案象征着坚冰出现裂纹并开始消融,寒冬已过,大地回春.冰裂纹图案形状无一定规则,图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则度.
 25. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若a=2,b=3,则该矩形的面积为.
25. 我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若a=2,b=3,则该矩形的面积为. 26. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是30,则这个风车的外围周长是.
26. 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边BC=5,将四个直角三角形中较长的直角边分别向外延长一倍,得到图2所示的“数学风车”,若△BCD的周长是30,则这个风车的外围周长是.
三、作图题
-
27. 下图是2002年在北京举办的世界数学家大会的会标“弦图”,它既标志着中国古代的数学成就,又像一只转动着的风车,欢迎世界各地的数学家们.
请将“弦图”中的四个直角三角形通过你所学过的图形变换,在以下方格纸中设计另个两个不同的图案.画图要求:(1)每个直角三角形的顶点均在方格纸的格点上,且四个三角形不重叠;(2)所设计的图案(不含方格纸)必须一个是中心对称图形,另一个是轴对称图形.

四、综合题
-
28. 新繁棕编是成都市新都区新繁镇的传统手工艺品之一,起源于清代嘉庆末年,早在200多年前就已走出国门,期间发现新繁棕编这一手工艺品新奇有趣,大为赞叹.于是甲乙两人均购买了部分产品打算回家赠送亲友,共花了215元,乙买了5个A类产品,共花了195元.(1)、求A类产品和B类产品的单价分别是多少元?(2)、该代表团考虑到端午节临近,决定投入不超过1550元给单位的每一位员工都买一个棕编作为端午节的慰问礼物之一,但要求购买的A类产品数量不超过B类产品的 , 请问该代表团共有几种购买方案?哪种方案费用最低?29. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有4000多年的历史,中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为活跃学生课余生活,欲购买一批象棋和围棋,已知购买3副象棋和1副围棋共需125元,购买2副象棋和3副围棋共需165元.(1)、求每副象棋和围棋的价格;(2)、若学校准备购买象棋和围棋总共100副,且总费用不超过3200元,则最多能购买多少副围棋?30. 阅读与思考
阅读下列材料并完成相应的任务.
我国是最早了解和应用勾股定理的国家之一,古代印度、希腊、阿拉伯等许多国家也都很重视对勾股定理的研究和应用,古希腊数学家毕达哥拉斯首先证明了勾股定理,在西方,勾股定理又称为“毕达哥拉斯定理”.关于勾股定理的研究还有一个很重要的内容是勾股数组,在课本中我们已经了解到“能够成为直角三角形三条边的三个正整数称为勾股数”.
以下是毕达哥拉斯等学派研究出的确定勾股数组的两种方法:
方法1:若m为奇数 , 则 , 和是勾股数.
方法2:若任取两个正整数m和 , 则 , , 是勾股数.
任务:
(1)、在以上两种方法中任选一种,证明以a,b,c为边长的是直角三角形.(2)、学校园林设计师按照如图所示的方式摆放兰花,已知这四个直角三角形全等,且直角三角形的三边是勾股数,较短的直角边长为 , 要求在每个直角三角形的三个顶点处需要摆放一盆兰花,每个直角三角形的三条边间隔1米摆放一盆兰花,请你计算出总共需要的兰花数量. 31. 阅读;在一杯水中,加入了食盐,搅拌均匀,就称作盐水.早在古代,人们就已经发现了这种水的存在.盐水可以消毒,是我们生活中常用物品,而且我们生病时所用的也是盐水(生理盐水),如果一容器内有a克盐水,其中含盐b克,则盐水的浓度= ×100%.(1)、公式应用:若容器中有80克盐水,其中含水60克,则盐水的浓度为;(2)、拓展延伸:若容器中有50克盐水,其中含盐5克,则需要蒸发多少克水,使该容器内的盐水浓度提高到原来的2倍;(3)、解决问题:若在装有盐水的容器中加入若干盐,食盐水的浓度怎么变化,为什么?(设该容器内原有a克盐水,其中含盐b克,再加入c克盐,用数学的方法书写过程).32. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家在节前用8000元购进猪肉粽和6000元购进的豆沙粽盒数相同.(1)、每盒豆沙粽和每盒猪肉粽的进价分别是多少元?(2)、商家计划在销售过程中,将猪肉粽的售价定为在进价的基础上提高25%,豆沙粽的售价定为每盒36元,进行销售,且按上述定价两种各售出了a盒后,将剩余的粽子均打九折出售.若要使得所有粽子售完且商家获利不低于2800元,则a的最小值是多少?33. 中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化.2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开晋商又以“万里茶道”著称.晋商古街某茶店用4000元购进了A种茶叶若干盒,又用8400元购进B种茶叶若干盒,若所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍;(1)、A,B两种茶叶每盒进价分别为多少元?(2)、第一次所购茶叶全部售完后,第二次购进A、B两种茶叶共100盒,(A、B进价不变,A种茶叶不少于20盒),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元,怎样进货才能获得最大利润?34. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往A,B,C三地销售,要求运往C地的袋数是运往A地袋数的3倍,各地的运费如下表所示:
31. 阅读;在一杯水中,加入了食盐,搅拌均匀,就称作盐水.早在古代,人们就已经发现了这种水的存在.盐水可以消毒,是我们生活中常用物品,而且我们生病时所用的也是盐水(生理盐水),如果一容器内有a克盐水,其中含盐b克,则盐水的浓度= ×100%.(1)、公式应用:若容器中有80克盐水,其中含水60克,则盐水的浓度为;(2)、拓展延伸:若容器中有50克盐水,其中含盐5克,则需要蒸发多少克水,使该容器内的盐水浓度提高到原来的2倍;(3)、解决问题:若在装有盐水的容器中加入若干盐,食盐水的浓度怎么变化,为什么?(设该容器内原有a克盐水,其中含盐b克,再加入c克盐,用数学的方法书写过程).32. 端午节是我国入选世界非物质文化遗产的传统节日,端午节吃粽子是中华民族的传统习俗.市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家在节前用8000元购进猪肉粽和6000元购进的豆沙粽盒数相同.(1)、每盒豆沙粽和每盒猪肉粽的进价分别是多少元?(2)、商家计划在销售过程中,将猪肉粽的售价定为在进价的基础上提高25%,豆沙粽的售价定为每盒36元,进行销售,且按上述定价两种各售出了a盒后,将剩余的粽子均打九折出售.若要使得所有粽子售完且商家获利不低于2800元,则a的最小值是多少?33. 中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化.2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开晋商又以“万里茶道”著称.晋商古街某茶店用4000元购进了A种茶叶若干盒,又用8400元购进B种茶叶若干盒,若所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍;(1)、A,B两种茶叶每盒进价分别为多少元?(2)、第一次所购茶叶全部售完后,第二次购进A、B两种茶叶共100盒,(A、B进价不变,A种茶叶不少于20盒),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元,怎样进货才能获得最大利润?34. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子是我省杂粮谷物中的大类.某小米经销商要将规格相同的1000袋小米运往A,B,C三地销售,要求运往C地的袋数是运往A地袋数的3倍,各地的运费如下表所示:
运往地
地
地
地
运费(元/袋)
20
10
15
(1)、设运往地的小米(袋),总运费为(元),试写出与的函数关系式;(2)、若总运费不超过15000元,最多可运往A地小米多少袋?35. “程,课程也,二物者二程,三物者三程,皆如物数程之,并列为行,故谓之方程.”这是我国古代著名数学家刘徽在《九章算术》对方程一词给出的注释,对于一些特殊的方程,我们给出两个定义:①若两个方程有相同的一个解,则称这两个方程为“相似方程”;②若两个方程有相同的整数解,则称这两个方程为“相伴方程”.(1)、判断分式方程与无理方程是否是“相似方程”,并说明理由;(2)、已知关于 , 的方程:和 , 它们是“相似方程”吗?如果是,请写出它们的公共解;如果不是,请说明理由;(3)、已知关于 , 的二元一次方程:和(其中为整数)是“相伴方程”,求的值.36. 阅读下列材料,解答后面的问题:我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,即已知三角形的三边长,求它的面积.用现代式子表示即为: ……①(其中 、 、 为三角形的三边长, 为面积).而另一个文明古国古希腊也有求三角形面积的“海伦公式”: ……②(其中 )(1)、若已知三角形的三边长分别为3,5,6,试分别运用公式①和公式②计算该三角形的面积 ;(2)、你能否由公式①推导出公式②?请试试写出推导过程.
-