命题新趋势1 数学文化——2024年浙教版数学八(下)期末复习
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 我国传统文化中的“福禄寿喜”图,属于美工艺术字分类,由四个图案构成.这四个图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. “二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图,其中文字上面图案是中心对称图形的是( )A、
2. “二十四节气”是中华上古农耕文明的智慧结晶.下列四幅标识图,其中文字上面图案是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕,年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中是中心对称图形的是( )A、
3. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕,年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 围棋起源于中国,古代称之为“弈”,至今已有多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )A、
4. 围棋起源于中国,古代称之为“弈”,至今已有多年的历史.一棋谱中四部分的截图由黑白棋子摆成的图案是中心对称的是( )A、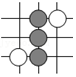 B、
B、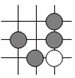 C、
C、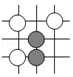 D、
D、 5. 春节期间,贴春联,送祝福一直是我们的优良传统.我国传统文化中的“福禄寿喜”图(如图)由四个图案构成.这四个图案中是中心对称图形的是( )A、
5. 春节期间,贴春联,送祝福一直是我们的优良传统.我国传统文化中的“福禄寿喜”图(如图)由四个图案构成.这四个图案中是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录,下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”,其中是中心对称图形的是( )A、
6. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录,下列四幅作品分别代表“清明”、“谷雨”、“白露”、“大雪”,其中是中心对称图形的是( )A、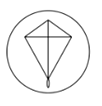 B、
B、 C、
C、 D、
D、 7. 国家级非物质文化遗产松桃苗绣,构图夸张浪漫,颜色素净淡雅,以花鸟虫鱼,飞禽走兽等为题材,体现苗族人民向往自由与和平的精神世界.以下四副苗绣图样中,是中心对称图形的是( )A、
7. 国家级非物质文化遗产松桃苗绣,构图夸张浪漫,颜色素净淡雅,以花鸟虫鱼,飞禽走兽等为题材,体现苗族人民向往自由与和平的精神世界.以下四副苗绣图样中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 瓦当,是指古代中国建筑中覆盖建筑檐头筒瓦前端的遮挡.瓦当上刻有文字、图案,也有用四方之神“朱雀”“玄武”“青龙”“白虎”做图案的.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( )
8. 瓦当,是指古代中国建筑中覆盖建筑檐头筒瓦前端的遮挡.瓦当上刻有文字、图案,也有用四方之神“朱雀”“玄武”“青龙”“白虎”做图案的.下面“瓦当”图案中既是轴对称图形又是中心对称图形的是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕、年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中,是轴对称图形,但不是中心对称图形的是( )A、
9. 剪纸艺术是最古老的中国民间艺术之一,先后入选中国国家级非物质文化遗产名录和人类非物质文化遗产代表作名录.鱼与“余”同音,寓意生活富裕、年年有余,是剪纸艺术中很受喜爱的主题.以下关于鱼的剪纸中,是轴对称图形,但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 10. 云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中.下列云纹图案中,是中心对称图形的是( )A、
10. 云纹,指云形纹饰,是古代中国吉祥图案,象征高升和如意,被广泛地运用于装饰中.下列云纹图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 11. 瓷器上的纹饰是中国古代传统文化的重要载体之一,下面花纹图案中既是轴对称图形又是中心对称图形的是( )A、
11. 瓷器上的纹饰是中国古代传统文化的重要载体之一,下面花纹图案中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 12. 窗棂即窗格(窗里面的横的、竖的或斜的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种化纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中,既是轴对称图形又是中心对称图形的是( )A、
12. 窗棂即窗格(窗里面的横的、竖的或斜的格)是中国传统木构建筑的框架结构设计,窗棂上雕刻有线槽和各种化纹,构成种类繁多的优美图案,下列表示我国古代窗棂样式结构图案中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 13. 我国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步.如果设宽为x步,则可列出方程( )A、 B、 C、 D、14. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,下列说法不一定成立的是( )
13. 我国古代数学家杨辉的《田亩比数乘除减法》中记载:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步?”翻译成数学问题是:一块矩形田地的面积为864平方步,它的宽比长少12步.如果设宽为x步,则可列出方程( )A、 B、 C、 D、14. 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(如图)”这一推论,他从这一推论出发,利用“出入相补”原理复原了《海岛算经》九题古证,下列说法不一定成立的是( ) A、 B、 C、 D、15. 农历五月初五是端午节,为继承和发扬民族优秀传统文化,某班组织“粽享文化”为主题的演讲比赛,比赛成绩由高到低设立一等奖1名,二等奖3名,三等奖5名,甲同学参加了演讲比赛,并且比赛成绩进入了前19名(比赛成绩都不相同),该同学想知道自己能否获奖,需比较自己的成绩与前19名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差16. 简简单单的七巧板能拼出千变万化的图形.殊不知七巧板作为中国传统玩具在国外也甚为流传,被称为“唐图”.下面四幅七巧板拼图的形状是中心对称图形的是( )A、
A、 B、 C、 D、15. 农历五月初五是端午节,为继承和发扬民族优秀传统文化,某班组织“粽享文化”为主题的演讲比赛,比赛成绩由高到低设立一等奖1名,二等奖3名,三等奖5名,甲同学参加了演讲比赛,并且比赛成绩进入了前19名(比赛成绩都不相同),该同学想知道自己能否获奖,需比较自己的成绩与前19名同学成绩的( )A、平均数 B、众数 C、中位数 D、方差16. 简简单单的七巧板能拼出千变万化的图形.殊不知七巧板作为中国传统玩具在国外也甚为流传,被称为“唐图”.下面四幅七巧板拼图的形状是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 17. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形.如图所示,已知 , 正方形ADOF的边长是2, , 则BD的长为( )
17. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形.如图所示,已知 , 正方形ADOF的边长是2, , 则BD的长为( ) A、6 B、 C、8 D、1018. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为 , 较长直角边为 , 那么的值为( ).
A、6 B、 C、8 D、1018. 2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小小正方形拼成的一个大正方形(如图所示),如果大正方形的面积是13,小正方形的面积是1,直角三角形的短直角边为 , 较长直角边为 , 那么的值为( ). A、13 B、19 C、25 D、16919. 我国古代著作《四元玉鉴》记载“买橡多少”问题:“六贯二百一十钱,遣人去买几株橡每株脚钱三文足,无钱准与一株椽.”其大意为现请人代买一批椽,这批椽的价钱为6 210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的橡的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、3(x-1)x=6210 B、3(x-1)=6210 C、(3x-1)x=6210 D、3x=6 21020. 勾股定理又称毕达哥拉斯定理、商高定理、新娘座椅定理、百牛定理等,是人类早期发现并证明的重要数学定理之一,大约有五百多种证明方法,我国古代数学家赵爽和刘徽也分别利用《赵爽弦图》和《青朱出入图》证明了勾股定理,以下四个图形,哪一个是赵爽弦图( )A、
A、13 B、19 C、25 D、16919. 我国古代著作《四元玉鉴》记载“买橡多少”问题:“六贯二百一十钱,遣人去买几株橡每株脚钱三文足,无钱准与一株椽.”其大意为现请人代买一批椽,这批椽的价钱为6 210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的橡的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )A、3(x-1)x=6210 B、3(x-1)=6210 C、(3x-1)x=6210 D、3x=6 21020. 勾股定理又称毕达哥拉斯定理、商高定理、新娘座椅定理、百牛定理等,是人类早期发现并证明的重要数学定理之一,大约有五百多种证明方法,我国古代数学家赵爽和刘徽也分别利用《赵爽弦图》和《青朱出入图》证明了勾股定理,以下四个图形,哪一个是赵爽弦图( )A、 B、
B、 C、
C、 D、
D、 21. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6 210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问不加运费6 210文能买多少株椽?设不加运费6 210文能买x株椽,则符合题意的方程是( )A、3(x-1)x=6210 B、3(x-1)=6210 C、(3x-1)x=6210 D、3x=621022. 《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几?”译文:“秋千静止的时候,踏板高地1尺,将它往前推送两步(两步=10尺)时,此时踏板升高到离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”如图,若设秋千绳索长为x尺,则可列方程为( )
21. 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6 210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问不加运费6 210文能买多少株椽?设不加运费6 210文能买x株椽,则符合题意的方程是( )A、3(x-1)x=6210 B、3(x-1)=6210 C、(3x-1)x=6210 D、3x=621022. 《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几?”译文:“秋千静止的时候,踏板高地1尺,将它往前推送两步(两步=10尺)时,此时踏板升高到离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”如图,若设秋千绳索长为x尺,则可列方程为( )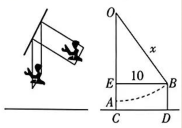 A、 B、 C、 D、23. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为的正方形沿对角线方向平移得到正方形 , 形成一个“方胜”图案,则点 , 之间的距离为( )
A、 B、 C、 D、23. “方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为的正方形沿对角线方向平移得到正方形 , 形成一个“方胜”图案,则点 , 之间的距离为( ) A、 B、 C、 D、24. 《2024年春节联欢晚会》以匠心独运的歌舞创编、暖心真挚的节目表演、充满科技感和时代感的视觉呈现,为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”.截至2月10日2时,总台春晚全媒体累计触达142亿人次,其中“竖屏看春晚”直播播放量4.2亿次.据统计,2022年首次推出的“坚屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为 , 则可列出关于的方程( )A、 B、 C、 D、25. 元宵节是我国的传统文化节日,做花灯、赏花灯是传统节日中的重要活动内容.小明在完成综合实践活动做花灯的过程中,花灯底部需要做一个对角线互相垂直的矩形铁丝网固定花灯的形状,该矩形铁丝网的面积为 , 则底部一条对角线所用的铁丝至少需( )
A、 B、 C、 D、24. 《2024年春节联欢晚会》以匠心独运的歌舞创编、暖心真挚的节目表演、充满科技感和时代感的视觉呈现,为海内外受众奉上了一道心意满满、暖意融融的除夕“文化大餐”.截至2月10日2时,总台春晚全媒体累计触达142亿人次,其中“竖屏看春晚”直播播放量4.2亿次.据统计,2022年首次推出的“坚屏看春晚”累计观看2亿次,设“竖屏看春晚”次数的年平均增长率为 , 则可列出关于的方程( )A、 B、 C、 D、25. 元宵节是我国的传统文化节日,做花灯、赏花灯是传统节日中的重要活动内容.小明在完成综合实践活动做花灯的过程中,花灯底部需要做一个对角线互相垂直的矩形铁丝网固定花灯的形状,该矩形铁丝网的面积为 , 则底部一条对角线所用的铁丝至少需( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
26. 《九章算术》是我国古代的数学名著,其中“勾股”章有一题,大意是说:已知矩形门的高比宽多 尺,门的对角线长 尺,那么门的高和宽各是多少?如果设门的宽为 尺,根据题意,那么可列方程 .27. 南吕是国家历史文化名城,其名源于“昌大南疆,南方昌盛”之意,市内的滕王阁、八一起义纪念馆、海昏侯遗址、绳金塔、八大山人纪念馆等都有深厚的文化底蕴、某班同学分小组到以上五个地方进行研学,人数分别为:12,5,11,5,7 (单位:人),这组数据的中位数是28. 图①是我国古代建筑中的一种窗格.其中冰裂纹图案象征着坚冰出现裂纹并开始消融,寒冬已过,大地回春.冰裂纹图案形状无一定规则,图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则度.
 29. 古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等”(如图1),问题解决:如图2,点P是矩形的对角线上一点,过点P作分别交 , 于点E,F,连接 , . 若 , , 则图中阴影部分的面积和为 .
29. 古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所得两长方形面积相等”(如图1),问题解决:如图2,点P是矩形的对角线上一点,过点P作分别交 , 于点E,F,连接 , . 若 , , 则图中阴影部分的面积和为 . 30. 中国结,象征着中华民族的历史文化与精神.利用所学知识抽象出如图所示的菱形 , 测得 , , 直线交两对边于E、F,则的长为cm.
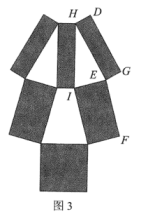
30. 中国结,象征着中华民族的历史文化与精神.利用所学知识抽象出如图所示的菱形 , 测得 , , 直线交两对边于E、F,则的长为cm. 31. 如图1是第32届夏季奥运会的会徽,它是由三种不同规格的全等矩形组成,代表了不同的国家、文化和思维方式,表达了多样性的融合.图2和图3为该会徽中的某一部分。如图2,三种矩形分别由三种不同的菱形依次连结各边中点得到,其中∠AOC=120°,∠AOB=90°.如图3,点D恰好在FE的延长线上,则∠IHE= 度.若AO=1,则点F,G之间的距离为
31. 如图1是第32届夏季奥运会的会徽,它是由三种不同规格的全等矩形组成,代表了不同的国家、文化和思维方式,表达了多样性的融合.图2和图3为该会徽中的某一部分。如图2,三种矩形分别由三种不同的菱形依次连结各边中点得到,其中∠AOC=120°,∠AOB=90°.如图3,点D恰好在FE的延长线上,则∠IHE= 度.若AO=1,则点F,G之间的距离为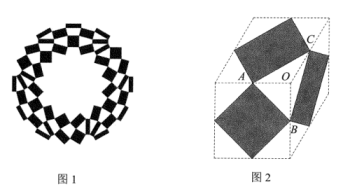
三、解答题
-
32. 如图,第十四届国际数学教育大会(ICME-14)会徽的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制数是3×83+7×82+4×81+5×80 =2021,表示ICME-14的举办年份.
 (1)、八进制数3746换算成十进制数是 .(2)、小华设计了一个n进制数143 ,换算成十进制数是120,求n的值.33. 如图1,荡秋千是中国古代北方少数民族创造的一种运动.有一天,小明在公园里游玩,如图2,他发现秋千静止时,踏板离地的垂直高度 , 将它往前推送(水平距离)时,秋千的踏板离地的垂直高度 , 秋千的绳索始终拉得很直,求绳索的长度?
(1)、八进制数3746换算成十进制数是 .(2)、小华设计了一个n进制数143 ,换算成十进制数是120,求n的值.33. 如图1,荡秋千是中国古代北方少数民族创造的一种运动.有一天,小明在公园里游玩,如图2,他发现秋千静止时,踏板离地的垂直高度 , 将它往前推送(水平距离)时,秋千的踏板离地的垂直高度 , 秋千的绳索始终拉得很直,求绳索的长度?
四、综合题
-
34. 我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何.(1丈=10尺)
大意是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?
将这个实际问题转化为数学问题,根据题意画出图形(如图所示),其中水面宽AB=10尺,线段CD,CB表示芦苇,CD⊥AB于点E.
 (1)、图中DE=尺,EB=尺;(2)、求水的深度与这根芦苇的长度.35. 湖笔是我国非物质文化遗产,尤其以善琏湖笔最为出名.某传统手工艺品网店准备在“6.18”网购节期间实施一系列优惠活动回馈新老客户,该店针对一款原价30元/支的湖笔推出了两种优惠方案:方案一、每支按8折销售;方案二、当购买数量超过40支但不超过60支时,每多购买1支单价减少0.5元,当购买数量超过60支时,每支单价为20元.(1)、购买数量为50支时,求方案二湖笔的单价;(2)、王老师准备在该网店购买x支湖笔赠与学生留念(已知x>40).
(1)、图中DE=尺,EB=尺;(2)、求水的深度与这根芦苇的长度.35. 湖笔是我国非物质文化遗产,尤其以善琏湖笔最为出名.某传统手工艺品网店准备在“6.18”网购节期间实施一系列优惠活动回馈新老客户,该店针对一款原价30元/支的湖笔推出了两种优惠方案:方案一、每支按8折销售;方案二、当购买数量超过40支但不超过60支时,每多购买1支单价减少0.5元,当购买数量超过60支时,每支单价为20元.(1)、购买数量为50支时,求方案二湖笔的单价;(2)、王老师准备在该网店购买x支湖笔赠与学生留念(已知x>40).①根据题意填写下表:(请用含x的代数式表示A和B)
方案
购买数量(支)
购买单价(元)
总金额(元)
方案一
x
24
24x
方案二
40<x≤60
A
B
x>60
20
20x
②王老师发现选择方案二比选择方案一可节省174元,求王老师购买湖笔所付的总金额.